第二篇[机器学习] 学习机器学习,从最简单的线性回归开始
机器学习,分为监督学习和无监督学习,监督学习里有回归和分类,分类有线性回归和逻辑回归。
从最简单的线性回归开始:
通过已有数据需要预测的线性方程:
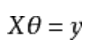
实际值和预测值的误差,求最小误差函数(最小二乘法):
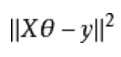
1.梯度下降法:
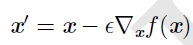
其中ε是步长,步长越大,下降越快,但是可能到不了局部最小值,步长越小,下降越慢,计算越多
2.正规方程直接求解:
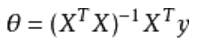
最小二乘法正规方程组的详细推导:
https://zhuanlan.zhihu.com/p/28190949?utm_medium=social&utm_source=wechat_session
scikit-learn的线性回归代码,参考网页:
input:
# Code source: Jaques Grobler # License: BSD 3 clause import matplotlib.pyplot as plt import numpy as np from sklearn import datasets, linear_model from sklearn.metrics import mean_squared_error, r2_score # Load the diabetes dataset diabetes = datasets.load_diabetes() # Use only one feature diabetes_X = diabetes.data[:, np.newaxis, 2] # Split the data into training/testing sets diabetes_X_train = diabetes_X[:-20] diabetes_X_test = diabetes_X[-20:] # Split the targets into training/testing sets diabetes_y_train = diabetes.target[:-20] diabetes_y_test = diabetes.target[-20:] # Create linear regression object regr = linear_model.LinearRegression() # Train the model using the training sets regr.fit(diabetes_X_train, diabetes_y_train) # Make predictions using the testing set diabetes_y_pred = regr.predict(diabetes_X_test) # The coefficients print('Coefficients: \n', regr.coef_) # The mean squared error print("Mean squared error: %.2f" % mean_squared_error(diabetes_y_test, diabetes_y_pred)) # Explained variance score: 1 is perfect prediction print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred)) # Plot outputs plt.scatter(diabetes_X_test, diabetes_y_test, color='black') plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3) plt.xticks(()) plt.yticks(()) plt.show()
output:
Coefficients: [ 938.23786125] Mean squared error: 2548.07 Variance score: 0.47
在这里,分别将diabetes_X_train和diabetes_y_train带入线性回归算法里拟合,求出了系数矩阵,并输出了均方误差和方差
怎么理解这里的系数,均方误差(MSE),方差?
coefficient,即系数矩阵
方差很简单,数据与平均数之差平方和的平均数
标准差是方差的平方根偏差,个别数据与平均值之差
均方误差,包含偏差和方差
偏差和方差的关系和机器学习容量,欠拟合和过拟合的概念联系比较紧密。
一般来说,偏差较大很可能欠拟合,方差较大可能过拟合。
在这里,我们使用的是最简单的线性回归模型,而且没有考虑怎么优化,没有考虑把数据进行分组进行交叉验证。
接下来,我会用这个模型分析kaggle上面的titanic数据,当然,结果肯定是很不好的,但是,重点是掌握这个方法,之后再考虑选择和优化。




