栈之中缀表达式转后缀表达式（逆波兰表达式）思路

一、前言

此篇只着重讲解中缀转后缀的过程，多次查阅他人讲解，都觉得讲解甚是云里雾里，记录思考过程，以便回顾，如有错误，欢迎指出，正确的知识总是在不断的知识碰撞中得出

二、 逻辑图示

 

 

 

三、 案例图解

1. 

 

根据上图所示

1.1 "9" 为操作数 -> 直接输出

 

 

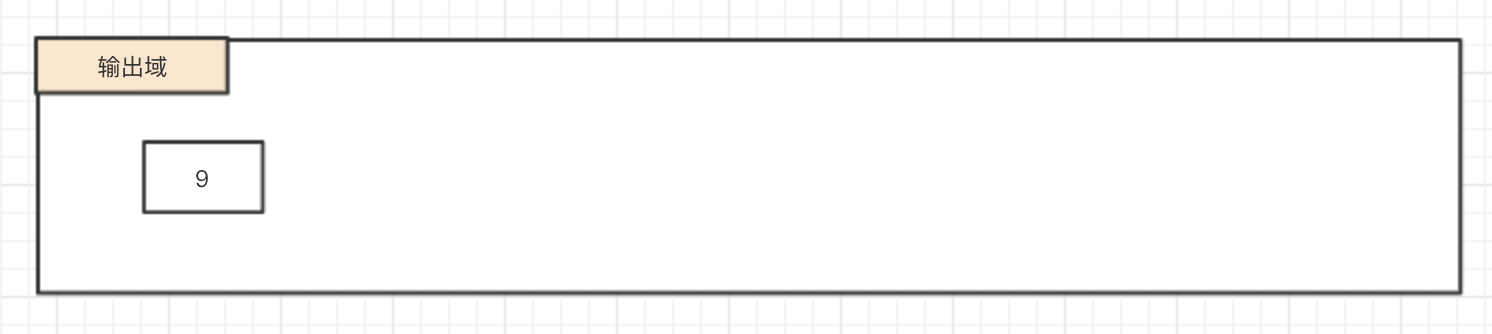
1.2 "+" 为操作符且不等于"(" || ")"且栈为空 -> 压栈

 

 1.3 "(" 直接-> 压栈

 

 1.4 "3" 为操作数 -> 输出

 

 1.5 "-" 位操作数，由于当前栈顶元素为左括号，不需要比较 -> 压栈

 

 

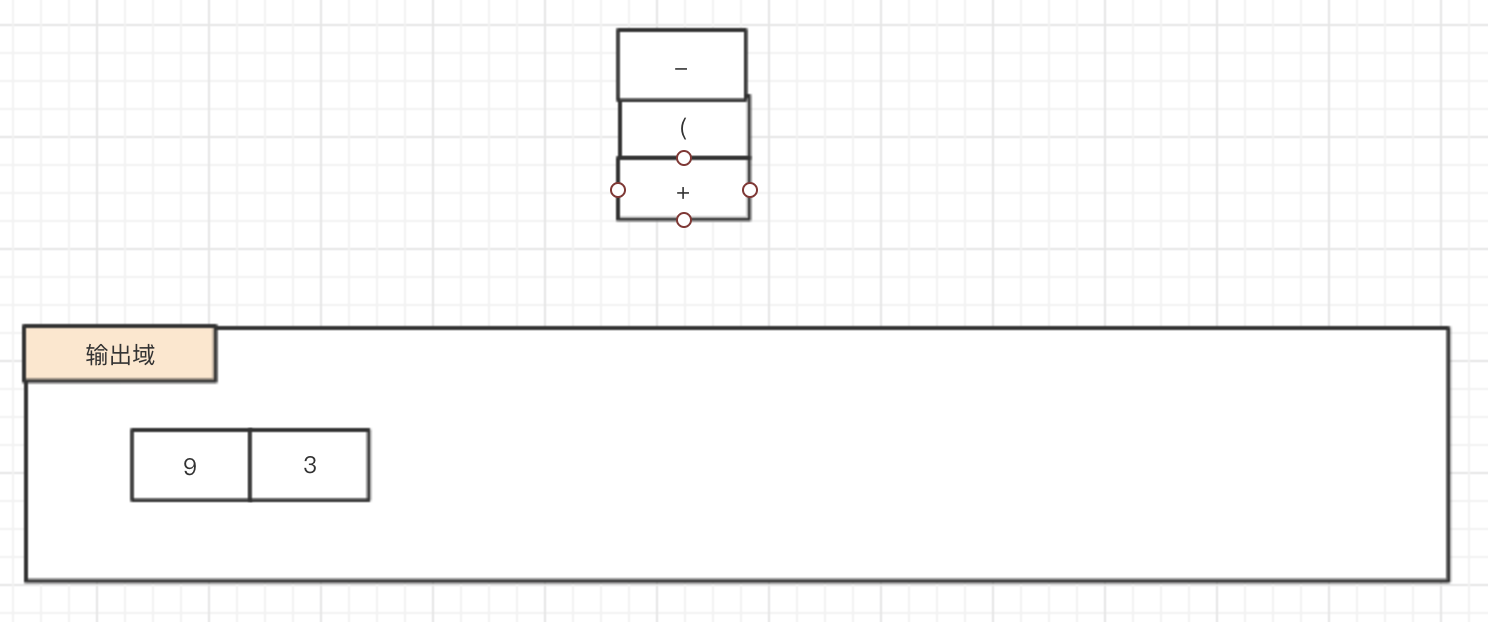
1.6  “1” -> 输出

 

 

 

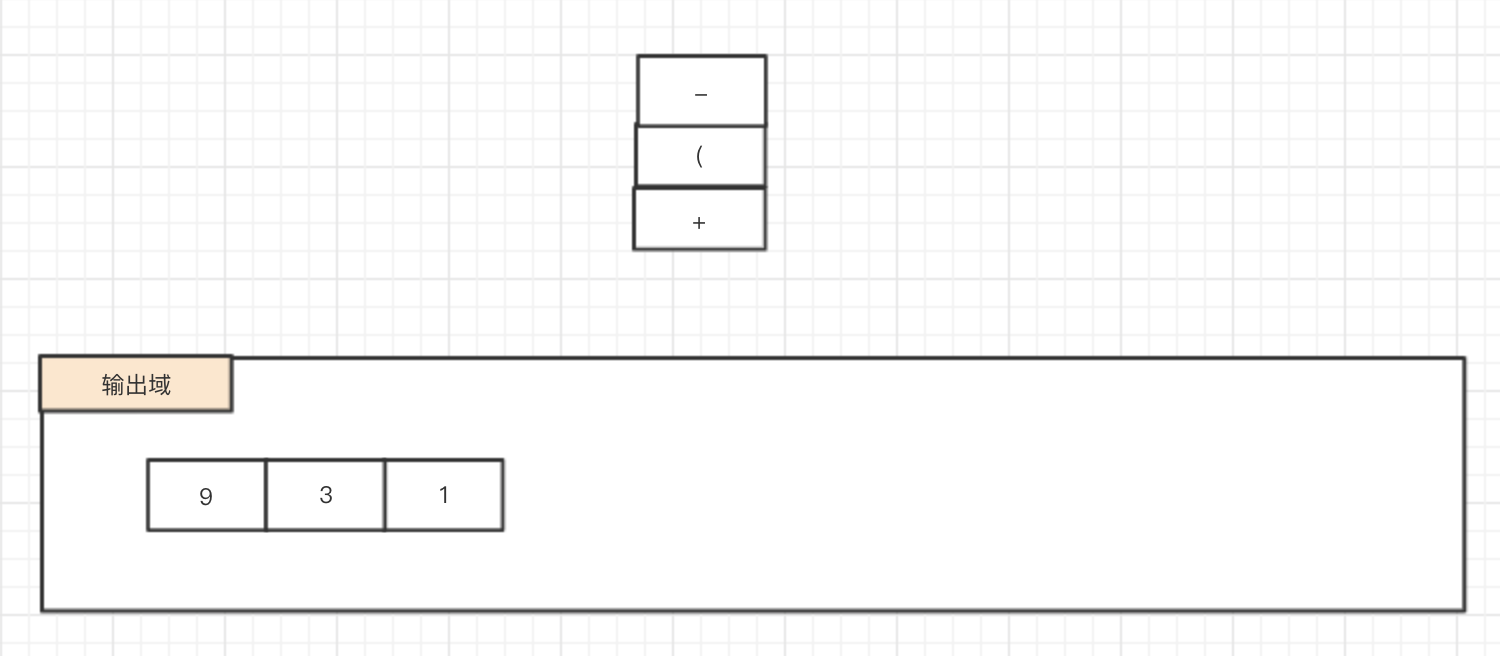
1.7 ")" ： 遇到右括号，此时将左括号上的元素依次弹出，并将弹出的元素除了左右括号之外依次输出

 

 

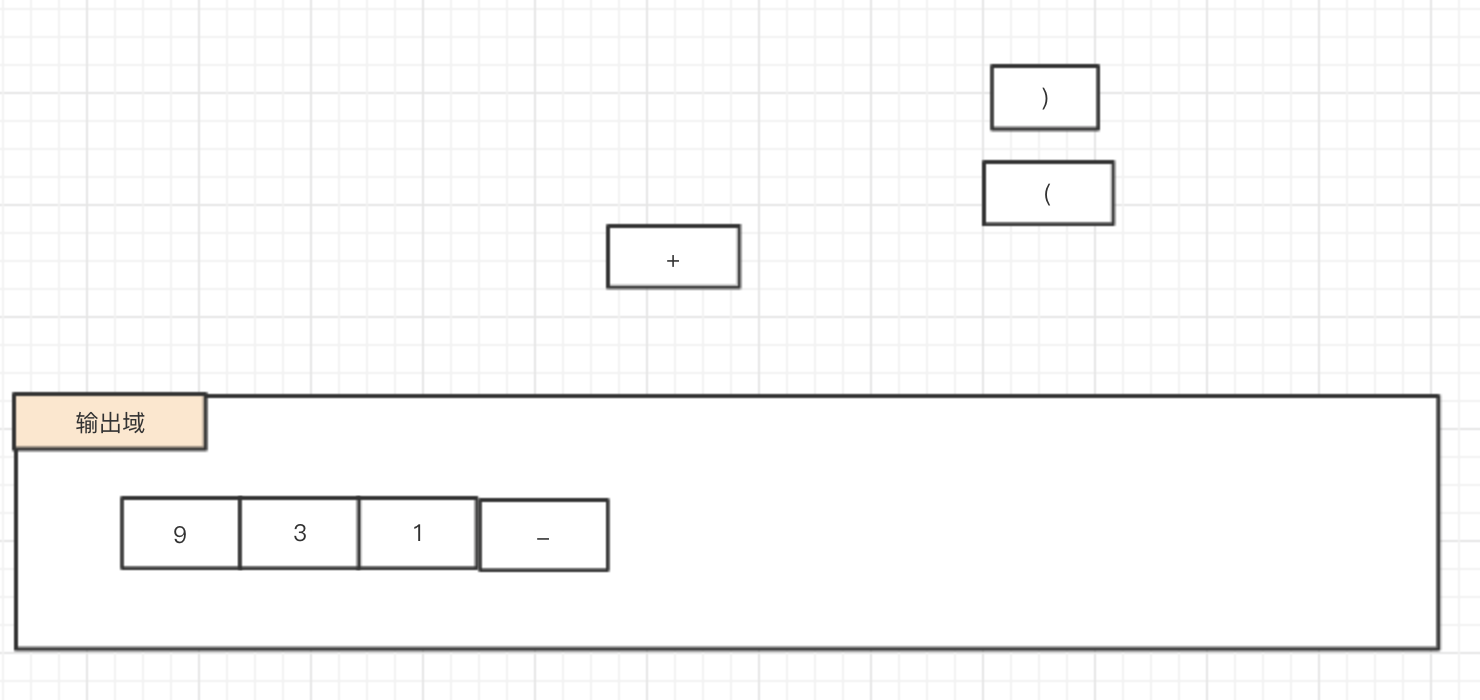
1.8  “*”： 此时操作符的优先级大于栈顶元素 -> 压栈

 

 

1.9 “3” -> 输出

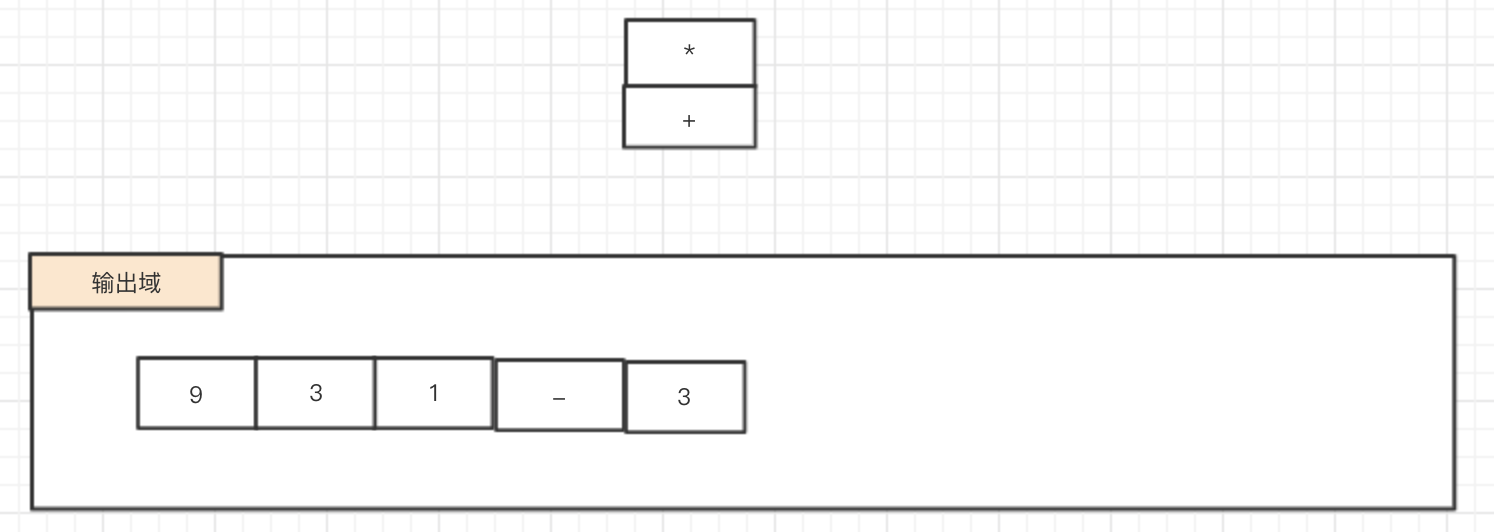
1.10 “+” ： 此时改操作符的优先级不大于栈顶，依次将比自己优先级打的操作符出栈，知道找到比自己优先级高的栈顶为止，这里由于 在栈内的元素分别是 “*” 和 “+” ，当前操作符 “+” 都小于这两个操作符，于是这两个操作符都依次出栈并输出，并将当前操作符入栈

 

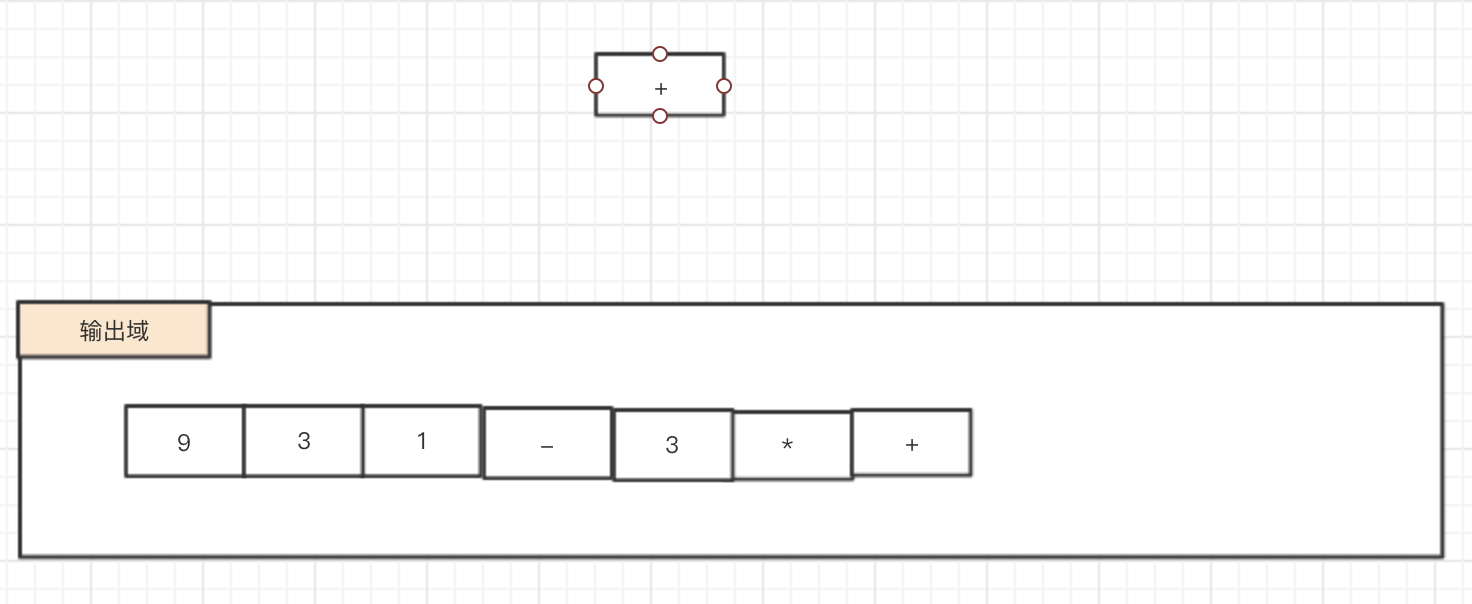
 1.11 "10" -> 输出

1.12 “/” 操作符优先级> 栈顶元素（“+”） -> 压栈

 

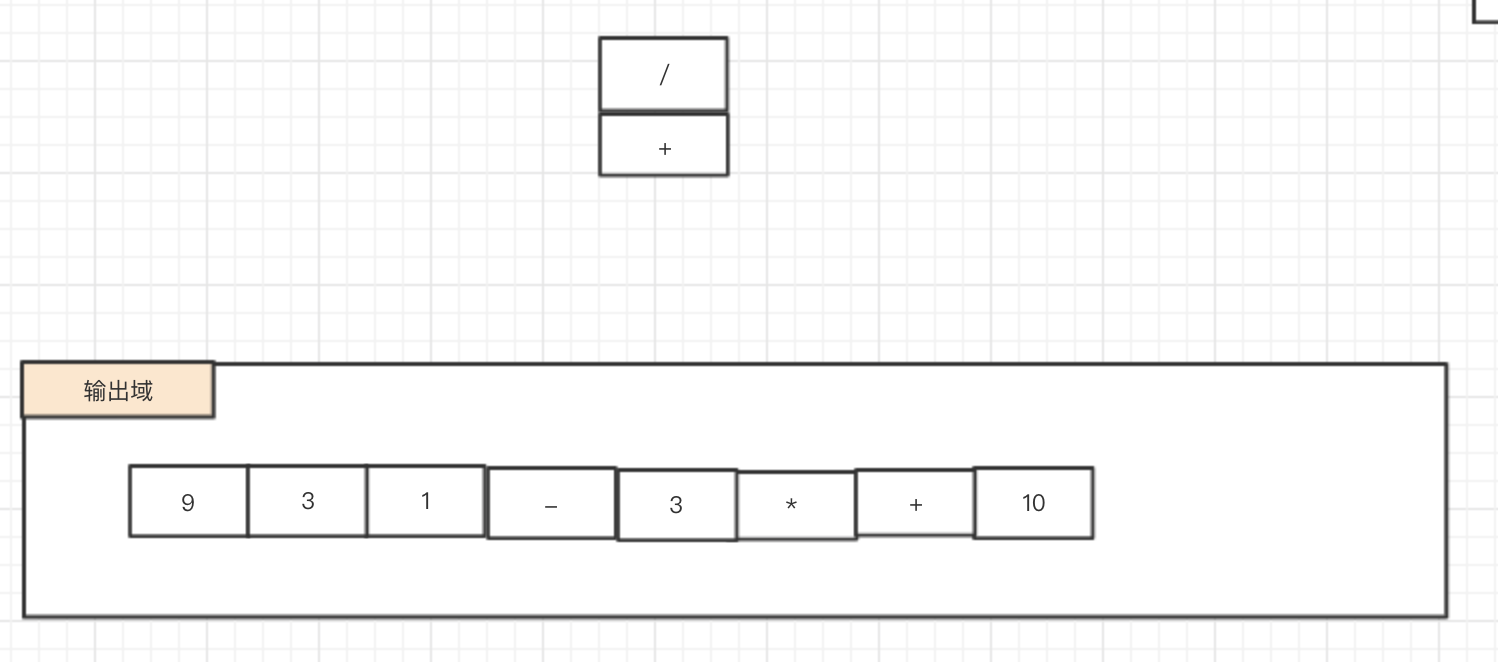
 1.13 “2” -> 输出

1.14 当元素都遍历完后，检查栈是否为空，如果非空，依次出栈并输出

 四、代码实现

实际上实现代码下来还是卡住了好久，这个点是当前值的优先级 小于 栈顶 要出栈的程序

function Stack() {
    var items = []; // 存储数据

    // 【压栈】从栈顶添加数据
    this.push = function(item){
        items.push(item)
    }

    // 从栈顶删除数据
    this.pop = function(){
        return items.pop()
    }

    // 获取栈顶元素
    this.top = function(){
        return items[items.length - 1]
    }

    // 判断栈是否为空
    this.isEmpty = function() {
        return items.length === 0
    }

    // 返回栈的大小
    this.size = function() {
        return items.length
    }

    // 清空栈
    this.clear = function() {
        items = []
    }

    // 打印栈元素
    this.content = function(){
        console.log('Stack>>', items)
    }
}


// 中缀转后缀

const priority_Map = {
    '+': '1',
    '-': '1',
    '*': '2',
    '/': '2'
}

function infix_exp_2_postfix_exp(exp) {
    // debugger
    let stack = new Stack()

    let postfix_exp = []

    for(let i = 0; i < exp.length; i++) {
        let item = exp[i]

        // 如果是数字 -> 输出
        if(/[0-9]/.test(item)) {
            postfix_exp.push(item)

        // 如果是左括号 -> 压栈
        } else if (/\(/.test(item)) {
            stack.push(item)

        // 如果是右括号 -> 出栈并输出直到item === '('    ,
        } else if(/\)/.test(item)) {

            while(!(stack.top() === '(')) {

                postfix_exp.push(stack.pop())
                
            }

            stack.pop()
            

        // 如果是操作符 -> 
        } else if(/[+|-|*|\/]/.test(item)) {

            // 如果栈为空 -> 压栈
            if(stack.isEmpty()){
                stack.push(item)

            // 如果栈顶元素的优先级为空（遇到左右括号） -> 压栈     
            } else if(!priority_Map[stack.top()]) {
                stack.push(item)    

            // item 优先级 > 栈顶优先级(成立): 压栈  ； 
            } else if(priority_Map[item] > priority_Map[stack.top()]) {
                stack.push(item)

            // item 优先级 > 栈顶优先级(不成立): 栈内元素出栈输出直到遇到item > 栈内元素的优先级, 当前元素压栈 ；    
            } else {

                // 首先确保是操作然后再进一步比较优先级大小，当当前item 优先级任然小于栈顶元素的优先级的时候就持续出栈输出
                while( priority_Map[stack.top()] && !(priority_Map[item] > priority_Map[stack.top()])) {
                    postfix_exp.push(stack.pop())
                }

                // 当前元素压栈
                stack.push(item)

            }
            
        } 

    }

    
    // 检查栈是否为空，如果不为空，就依次输出
    const stack_len = stack.size()
    for(let i = 0; i < stack_len; i++) {
        postfix_exp.push(stack.pop())
    }

    return postfix_exp
}

// console.log(infix_exp_2_postfix_exp(['12', '+', '3']))
// console.log(infix_exp_2_postfix_exp(['(', '1', '+', '(', '4', '+', '5', '+', '3', ')', '-', '3', ')', '+', '(', '9', '+', '8', ')']))
console.log(infix_exp_2_postfix_exp(['(', '1', '+', '(', '4', '+', '5', '+', '3', ')', '/', '4', '-', '3', ')', '+', '(', '6', '+', '8', ')', '*', '3']))

 

 

五、 总结

　　如果做到中缀转后缀后，可以往下做后缀的计算，大致思路是，如果是操作数就压栈，如果是操作符就连续出两个栈的数字并计算结果，将结果压栈