【转】四元数的推导过程

来自：https://blog.csdn.net/qq_28773183/article/details/80083607

四元数旋转推导过程

1.基本概念

(1) 四元数的一般形式如下:q=q0+q1i+q2j+q3kq=q0+q1i+q2j+q3k 
(2) 单位四元数:满足四元数的模为1,即q02+q12+q22+q32=1q02+q12+q22+q32=1 
(3) 四元数的三角形式:q=cosθ2+u⃗ sinθ2q=cosθ2+u→sinθ2 
(4)共轭四元数:q∗=q0−q1i−q2j−q3kq∗=q0−q1i−q2j−q3k 
(5) 纯四元数:q=q1i+q2j+q3kq=q1i+q2j+q3k 
(6)四元数与空间旋转:

 

Rq(p)=qpq−1Rq(p)=qpq−1

其中: 
qq:单位四元数 
q−1q−1:四元数的逆,对于单位四元数,q∗=q−1q∗=q−1 
pp:纯四元数 
Rq(p):也是一个纯四元数Rq(p):也是一个纯四元数

 

---

2. 欧拉角的万向锁问题

先看一个简单的欧拉旋转，如下图所示：欧拉旋转需要先确定旋转顺序，我们可以定义X-Y-Z的顺序（总共有12种旋转顺序），那么什么是万向锁呢，我们可以用手机在桌子上进行旋转，以手机的正面为xy平面，以手机的厚度的方向作为z轴，我们先绕x转一个角度，然后再绕y轴旋转90度，我们会发现一个问题，当我们再绕z轴旋转一个角度，效果等同于我开始绕x轴旋转另外一个角度,再绕y轴旋转90度就行了. 
 
我们的欧拉旋转只能表示二维空间了，这是解我们的微分方程会出现退化现象，造成我们的微分方程无法解的情况。这样说似乎还是比较模糊，那么我们举一个例子: 

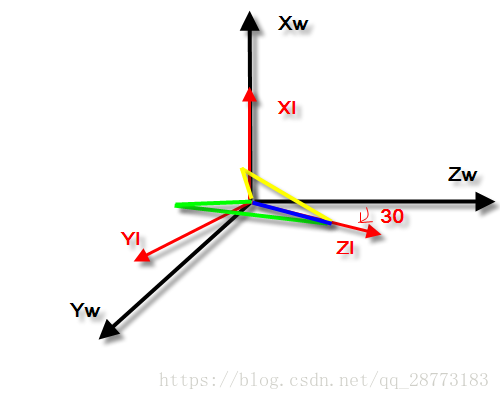
如图所示:XwYwZwXwYwZw是世界坐标系,XiYiZiXiYiZi是机体坐标系,我们先绕XiXi轴旋转30∘30∘,再绕YiYi旋转90∘90∘,如下图所示: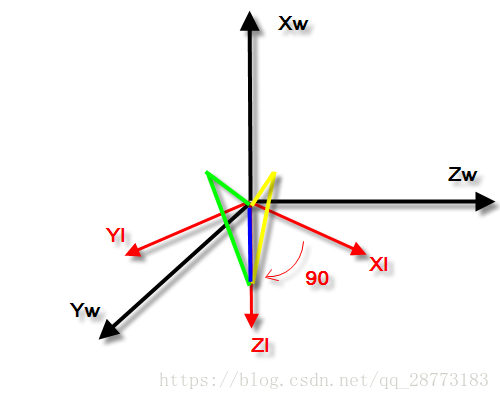 
 
此时我们的XwXw和ZiZi在同一直线上,最后我们再绕ZiZi旋转40∘40∘,如下图所示: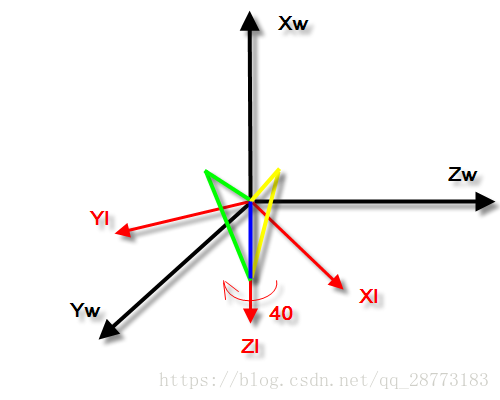 
 
我们会发现一个问题，无论我们怎么旋转，我们的坐标都是（30,90，z）,也就是绕z轴的旋转角度我们无法衡量的，这也就是我们的万向锁问题。

---

3. 四元数推导

复数旋转

首先我们看一个复数p=a+bip=a+bi在复平面的表示: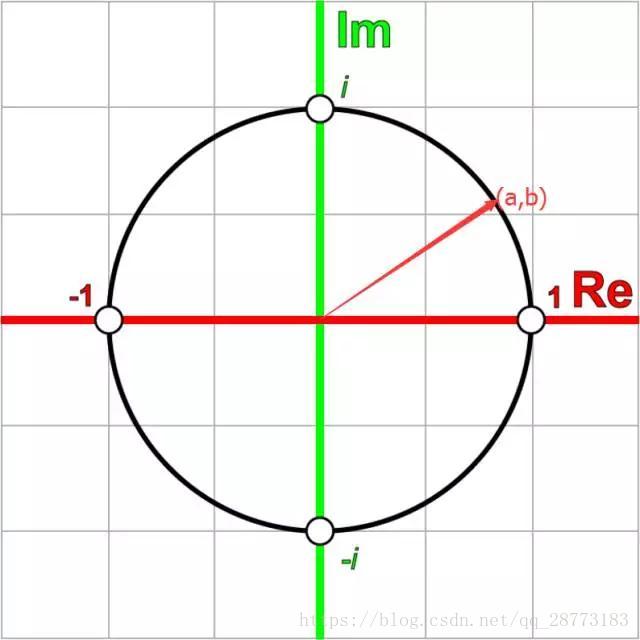 
现在我们将它旋转角度θθ,先定义另外一个复数q=cosθ+isinθq=cosθ+isinθ,我们发现,复数的乘法表示了一种旋转: 

 

qp=(acosθ−bsinθ)+i(asinθ+bcosθ)qp=(acosθ−bsinθ)+i(asinθ+bcosθ)

这个复数恰好就是pp旋转θθ角度后的值: 

 

三维复数旋转

我们看到了二维复数乘法可以表示旋转，那么三维空间呢。按照举一反三的思想，我们会想到再增加一个虚数作为第三个维度，这个就要涉及到我们的向量的叉乘，如下图所示： 
 
向量叉乘的结果是两个向量构成平面的垂直向量,那么我们定义两个个三维的复数: 

 

z1=a1+b1i+c1jz2=a2+b2i+c2jz1=a1+b1i+c1jz2=a2+b2i+c2j

其中i2=j2=−1i2=j2=−1,我们类似的进行复数的乘法,得到: 

 

z1z2=(a1a2−b1b2−c1c2)+(a1b2+a2b1)i+(a1c2+a2c1)j+b1c2ij+b2c1jiz1z2=(a1a2−b1b2−c1c2)+(a1b2+a2b1)i+(a1c2+a2c1)j+b1c2ij+b2c1ji

我们会发现,如果没有ij和jiij和ji这两项,我们三维的复数旋转也就没问题,那该如何处理呢?

 

四元数旋转

哈密尔顿引入四维的四元数:q=q0+q1i+q2j+q3k,其中i2=j2=k2=−1q=q0+q1i+q2j+q3k,其中i2=j2=k2=−1,根据向量的叉乘可以定义下列一些关系: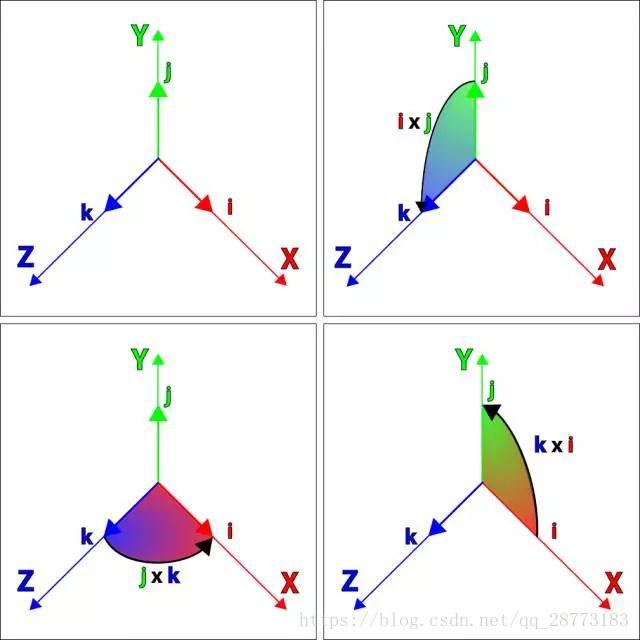 
 
 
 
 
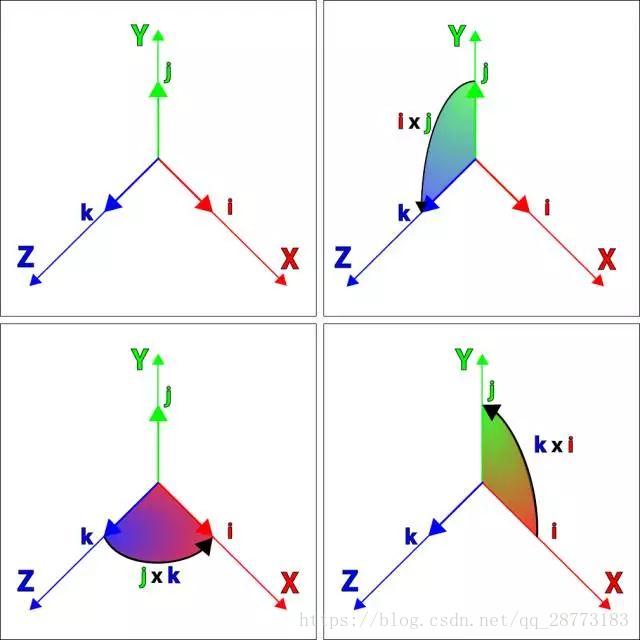
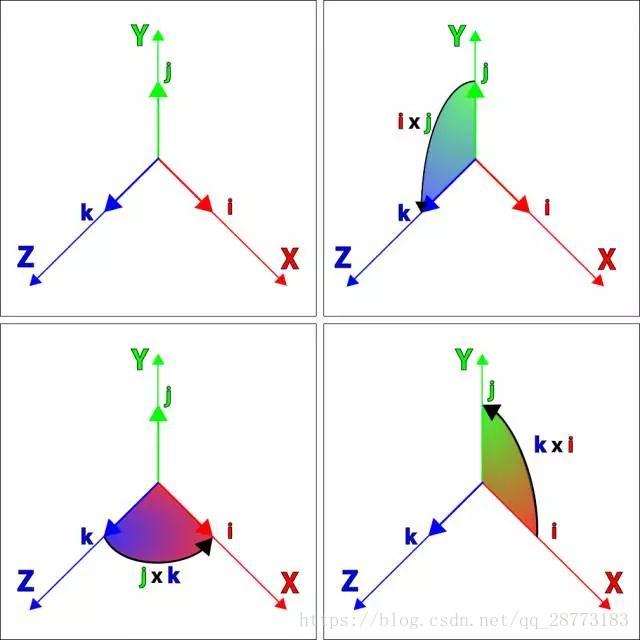
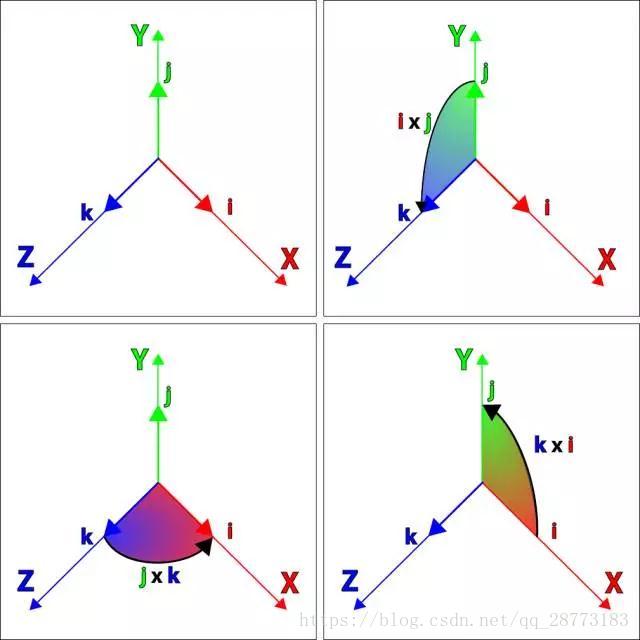
可以得到下列关系: 

 

ij=−ji=kjk=−kj=iki=−ik=ji2=j2=k2=ijk=−1ij=−ji=kjk=−kj=iki=−ik=ji2=j2=k2=ijk=−1

为了方便理解,我们将四元数写成向量的形式:q=[s,v⃗ ]q=[s,v→],我们可以理解为ss为实部,向量v⃗ v→表示的就是三维空间,下面我们看一下四元数的乘法: 

 

qa=[sa,a⃗ ]qb=[sb,b⃗ ]qaqb=[sasb−a⃗ ⋅b⃗ ,sab⃗ +sba⃗ +a⃗ ×b⃗ ]qa=[sa,a→]qb=[sb,b→]qaqb=[sasb−a→⋅b→,sab→+sba→+a→×b→]

由于我们研究的是三维空间,因此我们可以令qaqa为一个纯四元数,即qa=[0,a⃗ ]qa=[0,a→].则可以得到:

 

qaqb=[−a⃗ ⋅b⃗ ,sba⃗ +a⃗ ×b⃗ ]qaqb=[−a→⋅b→,sba→+a→×b→]

从上面可以看到,一个普通的四元数是无法将三维空间映射到三维空间的,我们令向量点乘的部分为零,此时,一个纯四元数就可以旋转为另一个纯四元数.为了表现出旋转,这里我们用四元数的三角表示方式:qb=[cosθ,sinθb⃗ ]qb=[cosθ,sinθb→],令a⃗ ⋅b⃗ =0a→⋅b→=0,则有: 

 

qaqb=[0,a⃗ cosθ+a⃗ ×b⃗ sinθ]qaqb=[0,a→cosθ+a→×b→sinθ]

我们没有对向量b⃗ b→做任何限制,下面来用一个例子说明应当对向量b⃗ b→做什么限制. 
令p=[0,2i],q=[2√2,2√2b⃗ ]p=[0,2i],q=[22,22b→],考虑到a⃗ ⋅b⃗ =0a→⋅b→=0,令b⃗ =|b⃗ |kb→=|b→|k,则将pp旋转45∘45∘后得到: 

 

p′=qp=[0,2–√|b⃗ |i+2–√|b⃗ |j]p′=qp=[0,2|b→|i+2|b→|j]

旋转之前,纯四元数pp的模长为|p|=2|p|=2,旋转过后,纯四元数p′p′的模长|p′|=2|b⃗ ||p′|=2|b→|,所以我们要给旋转四元数又加上一个约束:四元数qq的模长为1,即qq是一个单位四元数.

 

但是上面的旋转是有缺点的,因为其限制了我们的旋转轴和需要被旋转的四元数必须是垂直的(a⃗ ⋅b⃗ =0a→⋅b→=0),而不能达到任意的旋转.这时,聪明的哈密尔顿发现,一个四元数会把一个纯四元数拉到四维空间,但它的共轭又会把这个四维的空间拉回到三维空间.我们以一个简单的例子来说明这个问题: 

 

p=[0,2i],q=[fracsqrt22,fracsqrt66(i+j+k)],则q∗=[fracsqrt22,−fracsqrt66(i+j+k)]p=[0,2i],q=[fracsqrt22,fracsqrt66(i+j+k)],则q∗=[fracsqrt22,−fracsqrt66(i+j+k)]

旋转之后的四元数Rq(p)Rq(p): 

 

Rq(p)=[0,2j]Rq(p)=[0,2j]

这里需要注意的一点是,因为经过两次的旋转,所以旋转的角度是2θ2θ,这就是为什么我们常常看到的旋转四元数是一下形式: 

 

q=cosθ2+u⃗ sinθ2,其中|u⃗ |=1