【转】dijkstra算法

来自：https://blog.csdn.net/tw_345/article/details/50109375#comments

2015年11月30日 10:55:08

阅读数：1241

说到dijkstra，它其实是我第一个公司的Wi-Fi密码，当时我还不知道它就是求最短路径的一个算法。今天有幸能领略这位荷兰科学家的智慧～

Dijkstra算法是求某个源点到其他各顶点的最短路径的。

书本上的公式有点复杂，不如先看个例子再去理解公式～

 

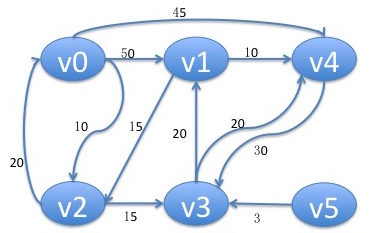
比如上图这道题（ppt画的，凑合看吧～）

运用dijkstra，求V0到各点的最短路径？

 

解答具体过程：

令S表示已求出最短路径的顶点集合。D［i］表示V0到Vi的路径长度。arcs[i][j]表示从i到j的直接距离

第一步：V0到其他顶点的直接路径：

 

S	D[1]	D[2]	D[3]	D[4]	D[5]
{V0}	50	10	∞	45	∞

下一步：计算min{D[i]}，得到D[2]最小，便将V2加入S中，得到V0V2最短路径10，重新计算V0到各点路径：

D[1](new) = min{D[1](old) ,D[2]+arcs[2][1]} ＝ min{50,10+∞}=50

D[3](new) = min{D[3](old) ,D[2]+arcs[2][3]} ＝ min{∞,10+15}=25

D[4](new) = min{D[4](old) ,D[2]+arcs[2][4]} ＝ min{45,10+∞}=45

D[5](new) = min{D[5](old) ,D[2]+arcs[2][5]} ＝ min{∞,10+∞}=∞

得到

S	D[1]	D[2]	D[3]	D[4]	D[5]
{V0，V2}	50		25	45	∞

下一步：（也不能说下一步，反正就是循环）计算min{D[i]}，D[3]最小，V3加入S中，得到V0V3最短路径25，重新计算路径：

D[1](new) = min{D[1](old) ,D[3]+arcs[3][1]} ＝ min{50,25+20}=45

D[4](new) = min{D[4](old) ,D[3]+arcs[3][4]} ＝ min{45,25+20}=45

D[5](new) = min{D[5](old) ,D[3]+arcs[3][5]} ＝ min{∞,25+∞}=∞

得到

S	D[1]	D[2]	D[3]	D[4]	D[5]
{V0，V2，V3}	45			45	∞

怎么样？是不是很带感

下一步：计算min{D[i]}，D[1]（看1比较顺眼）最小，V1加入S中，得到V0V1最短路径45，重新计算路径：

D[4](new) = min{D[4](old) ,D[1]+arcs[1][4]} ＝ min{45,45+10}=55

D[5](new) = min{D[5](old) ,D[1]+arcs[1][5]} ＝ min{∞,45+∞}=∞

得到

S	D[1]	D[2]	D[3]	D[4]	D[5]
{V0,V2,V3,V1}				45	∞

下一步：计算min{D[i]}，D[4]最小，V4加入S中，得到V0V4最短路径45，重新计算路径：

D[5](new) = min{D[5](old) ,D[4]+arcs[4][5]} ＝ min{∞,45+∞}=∞

得到

S	D[1]	D[2]	D[3]	D[4]	D[5]
{V0,V2,V3,V1,V4}					∞

得到V0V5最短路径∞，

所以最短路径为

 

V0V1	45
V0V2	10
V0V3	25
V0V4	45
V0V5	∞

Dijkstra算法的基本思想是：按最短路径长度递增的顺序，逐个产生各最短路径。

那么如何递增呢？其实是运用一条性质：如果存在一条从i到j的最短路径(Vi.....Vk,Vj)，Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。

然而这条性质是如何得到呢，这就需要我们先弄清楚最短路径的“最优子结构性质”。

最优子结构性质：如果P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径，k和s是这条路径上的一个中间顶点，那么P(k,s)必定是从k到s的最短路径。下面用反证法证明：

假设P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径，则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离，那么

必定存在另一条从k到s的最短路径P'(k,s)，那么P'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。

 

好了，铺垫的差不多了，Dijkstra就提出了以最短路径长度递增，逐次生成最短路径的算法。譬如对于源顶点V0，首先选择其直接相邻的顶点中长度最短的顶点Vi（注意相邻和最短），那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+arcs[i][j]}。

根据这种思路，假设存在G=<V,E>，源顶点为V0，S={V0}, dist[i]记录V0到Vi的最短距离，path[i]记录从V0到Vi路径上的Vi前面的一个顶点。

1.从不在S的V中选择使dist[i]值最小的顶点i，将i加入到S中；

2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+matrix[i][j]})；（上例是全部更新，不直接相邻就用“∞”表示）

3.直到S=V。

代码实现:（代码来源于网络）

 

1.  
   #include <iostream>
2.  
   #include<stack>
3.  
   #define M 100
4.  
   #define N 100
5.  
   using namespace std;
6.  
    
7.  
   typedef struct node
8.  
   {
9.  
   int matrix[N][M]; //邻接矩阵
10.  
    int n; //顶点数
11.  
    int e; //边数
12.  
    }MGraph;
13.  
     
14.  
    void DijkstraPath(MGraph g,int *dist,int *path,int v0) //v0表示源顶点
15.  
    {
16.  
    int i,j,k;
17.  
    bool *visited=(bool *)malloc(sizeof(bool)*g.n);
18.  
    for(i=0;i<g.n;i++) //初始化
19.  
    {
20.  
    if(g.matrix[v0][i]>0&&i!=v0)
21.  
    {
22.  
    dist[i]=g.matrix[v0][i];
23.  
    path[i]=v0; //path记录最短路径上从v0到i的前一个顶点
24.  
    }
25.  
    else
26.  
    {
27.  
    dist[i]=INT_MAX; //若i不与v0直接相邻，则权值置为无穷大
28.  
    path[i]=-1;
29.  
    }
30.  
    visited[i]=false;
31.  
    path[v0]=v0;
32.  
    dist[v0]=0;
33.  
    }
34.  
    visited[v0]=true;
35.  
    for(i=1;i<g.n;i++) //循环扩展n-1次
36.  
    {
37.  
    int min=INT_MAX;
38.  
    int u;
39.  
    for(j=0;j<g.n;j++) //寻找未被扩展的权值最小的顶点
40.  
    {
41.  
    if(visited[j]==false&&dist[j]<min)
42.  
    {
43.  
    min=dist[j];
44.  
    u=j;
45.  
    }
46.  
    }
47.  
    visited[u]=true;
48.  
    for(k=0;k<g.n;k++) //更新dist数组的值和路径的值
49.  
    {
50.  
    if(visited[k]==false&&g.matrix[u][k]>0&&min+g.matrix[u][k]<dist[k])
51.  
    {
52.  
    dist[k]=min+g.matrix[u][k];
53.  
    path[k]=u;
54.  
    }
55.  
    }
56.  
    }
57.  
    }
58.  
     
59.  
    void showPath(int *path,int v,int v0) //打印最短路径上的各个顶点
60.  
    {
61.  
    stack<int> s;
62.  
    int u=v;
63.  
    while(v!=v0)
64.  
    {
65.  
    s.push(v);
66.  
    v=path[v];
67.  
    }
68.  
    s.push(v);
69.  
    while(!s.empty())
70.  
    {
71.  
    cout<<s.top()<<" ";
72.  
    s.pop();
73.  
    }
74.  
    }
75.  
     
76.  
    int main(int argc, char *argv[])
77.  
    {
78.  
    int n,e; //表示输入的顶点数和边数
79.  
    while(cin>>n>>e&&e!=0)
80.  
    {
81.  
    int i,j;
82.  
    int s,t,w; //表示存在一条边s->t,权值为w
83.  
    MGraph g;
84.  
    int v0;
85.  
    int *dist=(int *)malloc(sizeof(int)*n);
86.  
    int *path=(int *)malloc(sizeof(int)*n);
87.  
    for(i=0;i<N;i++)
88.  
    for(j=0;j<M;j++)
89.  
    g.matrix[i][j]=0;
90.  
    g.n=n;
91.  
    g.e=e;
92.  
    for(i=0;i<e;i++)
93.  
    {
94.  
    cin>>s>>t>>w;
95.  
    g.matrix[s][t]=w;
96.  
    }
97.  
    cin>>v0; //输入源顶点
98.  
    DijkstraPath(g,dist,path,v0);
99.  
    for(i=0;i<n;i++)
100.  
     {
101.  
     if(i!=v0)
102.  
     {
103.  
     showPath(path,i,v0);
104.  
     cout<<dist[i]<<endl;
105.  
     }
106.  
     }
107.  
     }
108.  
     return 0;
109.  
     }

110.