图像灰度直方图均衡和线性变换
灰度变换是指根据某种目标条件,按一定变换关系逐点改变源图像中每一个像素灰度值的方法,目的是为了改善画质,使图像的显示效果更加清晰。图像的灰度变换处理是图像增强处理技术中的一种非常基础、直接的空间域图像处理方法,也是图像数字化软件和图像显示软件的一个重要组成部分。
本文通过实现直方图均衡和线性变换分别对图像进行处理,研究其原理及效果。
1. 直方图均衡
算法流程
- 统计各灰度级的像素点个数,并计算从 0 到 255 的累积值。
- 根据频率的累积分布计算得到各灰度级变换后的灰度级。
- 对原图像的每个像素点进行映射变换。
主要代码
void equalizeHist(const Mat &srcImg, Mat &dstImg) {
dstImg.create(srcImg.size(), srcImg.type());
uchar *srcImgData = srcImg.data;
uchar *dstImgData = dstImg.data;
int *hist = new int[256];
memset(hist, 0, 256 * sizeof(int));
int pixNum = srcImg.cols * srcImg.rows;
for (int i = 0; i < pixNum; i++)
hist[srcImgData[i]]++;
for (int i = 1; i < 256; i++)
hist[i] += hist[i-1];
uchar *map = new uchar[256];
for (int i = 0; i < 256; i++)
map[i] = cvRound((double)hist[i] / pixNum * 255);
for (int i = 0; i < pixNum; i++)
dstImgData[i] = map[srcImgData[i]];
}
参数说明:
srcImg:原图像dstImg:直方图均衡后的图像
运行结果分析
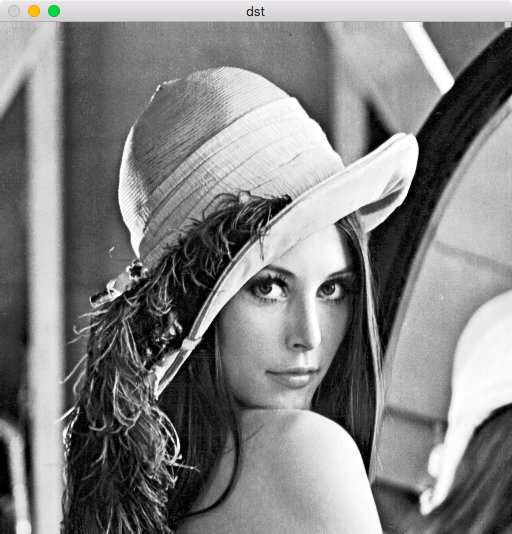
首先对 Lena 的这张经典人物肖像进行测试,可以看到直方图均衡后的图片有了明显的变化,亮度分布更加均匀,对比度得到增强。
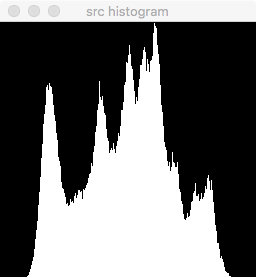
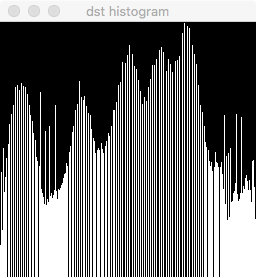
为了更加直观地观察灰度的变化,把均衡前后的直方图也生成出来,发现灰度的分布的确变得均匀了。
 |
 |
 |
 |
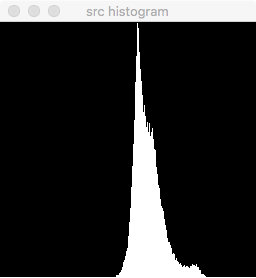
在这张风景图上,直方图均衡的效果更加明显,原本像是蒙了一层纱的画面变得清晰,更多局部细节被显现出来。
 |
 |
 |
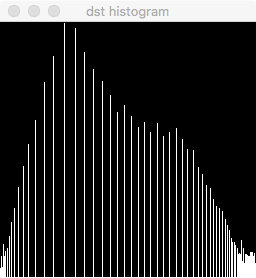 |
2. 线性变换
算法流程
- 计算各灰度级做线性变换后的灰度级。
- 对原图像的每个像素点进行映射变换。
主要代码
void linearTransform(const Mat &srcImg, Mat &dstImg, double k, double b) {
dstImg.create(srcImg.size(), srcImg.type());
uchar *srcImgData = srcImg.data;
uchar *dstImgData = dstImg.data;
uchar *map = new uchar[256];
for (int i = 0; i < 256; i++) {
int temp = cvRound(k * i + b);
if (temp > 255) temp = 255;
else if (temp < 0) temp = 0;
map[i] = temp;
}
int pixNum = srcImg.cols * srcImg.rows;
for (int i = 0; i < pixNum; i++)
dstImgData[i] = map[srcImgData[i]];
}
参数说明:
srcImg:原图像dstImg:直方图均衡后的图像k:斜率b:截距
运行结果分析
观察了一些图片后不难注意到,那些视觉效果不太好的图像往往都是灰蒙蒙的,在直方图上表现出灰度大量集中在中间区域,而两边最黑和最白的等级却几乎没有。由此很自然地联想到,雾霾天拍摄的图像也是这样的质感,是否可以通过线性变换的方法拉伸灰度分布的范围,从而尽可能地还原图像的信息呢?
这里用两张雾霾天的图像进行说明。
图像一:k = 3.4 b = -280.0
 |
 |
 |
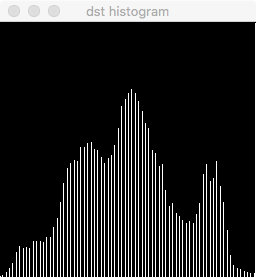 |
图像二:k = 3.2 b = -350.0
 |
 |
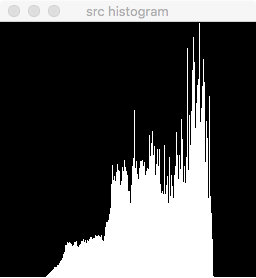 |
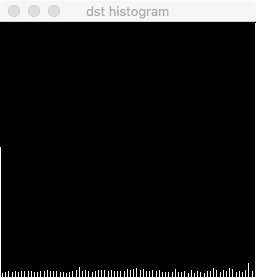 |
可以看到线性变换的效果还是非常明显的,原本被雾霾隐去的信息一定程度上显现了出来。
关于参数
以上两张图线性变换后的图像都是经过多次试验后得到的,参数 k 和 b 的选择是变换后图像效果好坏的关键。在进行了更多图像的试验后,总结出以下几点:
k > 1,拉伸灰度分布,图像对比度增加;0 < k < 1,压缩灰度分布,图像对比度减小;b > 0,灰度值向上平移,图像整体变亮;b < 0,灰度值向下平移,图像整体变暗。
对于上述两张图像,我们需要增强其对比度,因此 k > 1 ,至于具体取多少,要根据图像原本的灰度分布。比如第一张图像灰度分布很集中,因此 k 要大一些;而第二张图像灰度分布得更宽一些,因此 k 应该适当取小一点。参数 b 的作用是使灰度整体平移,调节由于对比度增强导致的灰度偏移,使得灰度大致分布在中央的位置。
事实上第二张图像为了尽可能地增大对比度,参数 k 已经取得相对过大了。由于代码中对小于 0 和大于 255 的灰度值进行了截断,因此直方图中显示出大量的像素点集中在灰度为 0 和 255 的两侧,而中间的灰度值却很少。在图像中表现为原本不同等级的较黑的区域全部变成最黑,同时不同等级的较白的区域全部变成最白,从而可能导致某些信息的丢失,这就是 k 取值过大的弊端。
总的来说,首先要根据灰度原本的分布取一个尽可能大而又不至于导致灰度两侧堆积的 k ,然后通过调节 b 使得灰度分布在中央。如果线性变换后灰度分布均衡地占满了所有的灰度等级,那么图像的视觉效果应当是比较好的。
3. 总结
直方图均衡和线性变换都可以使图像的对比度得到增强,从而显示出更多的细节信息,一定程度上起到改善图像视觉效果的作用。而后者由于参数可调,因而对图像的处理更加自由,例如分段线性变换还可以根据感兴趣的灰度区间,对不同的灰度范围进行不同的映射处理。
完整源码请见 GitHub 仓库



