[原]有限域的多项式乘法逆元求解
题目:

求解算法,扩展的欧几里得算法
/*
@author tilltheendwjx
@blog http://blog.csdn.net/wjh200821或者http://www.cnblogs.com/tilltheendwjx/
*/
#include<iostream>
using namespace std;
int indexofmax1(int value)
{
int tmp=1;
int count=0;
for(int i=0;i<sizeof(int)*8;++i)
{
if((value&tmp))
count=i;
tmp=tmp*2;
}
return count;
}
void polynomialtostring(int value)
{
int tmp=1;
int flag=0;
int c=indexofmax1(value);
for(int i=0;i<sizeof(int)*8;++i)
{
if((value&tmp))
{
if(i==0)
{
cout<<"1";
}else if(i==1)
{
cout<<"x";
}else
{
cout<<"x^"<<i;
}
flag=1;
if(i<c)
cout<<"+";
}
tmp=tmp*2;
}
if(flag==0)
cout<<"0";
}
int powofvalue(int value)
{
return 1<<(value);
}
int divide(int m,int b,int &remainvalue)
{
int mindex=indexofmax1(m);
int vindex=indexofmax1(b);
if(mindex<vindex)
{
remainvalue=m;
return 0;
}
int c=mindex-vindex;
int tmp=b;
tmp=tmp<<c;
m=m^tmp;
return powofvalue(c)|divide(m,b,remainvalue);
}
int Tx(int ax,int q,int bx)
{
//cout<<endl;
//cout<<ax<<"\t"<<bx<<"\t";
int tmp=1;
int value=0;
for(int i=0;i<sizeof(int)*8;++i)
{
if((q&tmp))
{
value=value^((bx<<i));
}
tmp=tmp*2;
}
//cout<<ax<<"\t"<<value<<"\t";
//cout<<endl;
return ax^(value);
}
int extent_gcd(int m,int b,int &x,int &y)
{
int a1=1,a2=0,a3=m;
int b1=0,b2=1,b3=b;
int remainvalue=0;
while(1)
{
polynomialtostring(a1);
cout<<" ";
polynomialtostring(a2);
cout<<" ";
polynomialtostring(a3);
cout<<" ";
polynomialtostring(b1);
cout<<" ";
polynomialtostring(b2);
cout<<" ";
polynomialtostring(b3);
cout<<" ";
if(b3==0)
return a3;
if(b3==1)
return b3;
int q=divide(a3,b3,remainvalue);
int t1=Tx(a1,q,b1);
int t2=Tx(a2,q,b2);
int t3=remainvalue;
cout<<t1<<endl;
cout<<t2<<endl;
a1=b1;a2=b2;a3=b3;
b1=t1;b2=t2;b3=t3;
x=b2;y=b3;
polynomialtostring(q);
cout<<endl;
}
}
int main(void)
{
int m=283,b=83,x=0,y=0;
cout<<"中间结果如下:"<<endl;
cout<<"a1 a2 a3 b1 b2 b3 q"<<endl;
int reault=extent_gcd(m,b,x,y);
cout<<endl;
cout<<"多项式(";polynomialtostring(b);cout<<")mod(";polynomialtostring(m);cout<<")的乘法逆元是(";polynomialtostring(x);cout<<")"<<endl;
system("pause");
return 0;
}
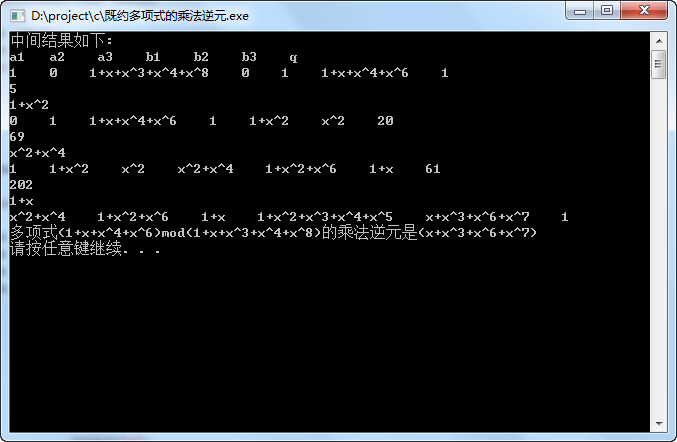
运行结果如下图
作者:wjh200821 发表于2012-5-15 22:13:00 原文链接
阅读:2 评论:0 查看评论
posted on 2012-05-15 22:13 tilltheendwjx 阅读(7187) 评论(0) 编辑 收藏 举报



