计算机为什么要搞出“补码”这种东西？

计算机为什么要搞出“补码”这种东西？

本文阐述两个问题

①计算机为什么要搞出个“补码”？不嫌麻烦？

②为什么-128的补码是10000000?

---

计算机为什么要搞出个“补码”？

先回顾一下补码是什么：
|--正数的补码是其本身(二进制原码)
|--负数的补码是在原码的基础上，符号位不变，其余位取反后加1。
为什么好好的“原码”不用，非搞个“补码”出来？顺带还迁出个“反码”……

究其原因，主要是因为计算机只会做加法，使用补码可以把减法转为加法计算。
关于计算机不会做加法，我们要表示理解，毕竟是那种国家发明的……

其实你也未必会做减法呀……

好了，言归正传，回到计算机的世界。
举个简单的例子：1-1=0
|--如果让计算机计算这个简单的算术，它只能转成加法：(1)+(-1)，
|--如果按二进制直接算（即按原码算，左一是符号位）

• 二进制( 1)： 0000 0001

• 二进制(-1)： 1000 0001

• 按位加等于：1000 0010

换为十进制是(-2)，谬矣！

如果用补码算：

(1)是正数，的补码还是0000 0001

(-1)先求反码，符号位不变，其余位取反：1000 0001→1111 1110

末位加1，得1111 1111

于是有以下两数相加：

• 0000 0001
• 1111 1111

得到：[1]0000 0000

左侧进位的1舍弃，该数就是0，计算正确。

所以，补码的作用就是：把减法转成加法进行计算。

---

为什么-128的补码是10000000?

二进制1000 0000表示的有符号数是-128，这个也很奇怪：

荒谬①：-128按规则求补码应该是[1] 1000 0000，已经溢出，未溢出的左一为符号位，其他位数取反得1111 1111，末位加1，得0000 0000，这是0的原码！

荒谬②：按补码的性质，1000 0000符号位为1，是负数；逆推原码先推反码，需末位-1，成了0000 0001，符号位为0，成正数了，自相矛盾，不用继续。

所以1000 0000无法按照补码规则推断源码，

它是-128的补码是一个“规定”。

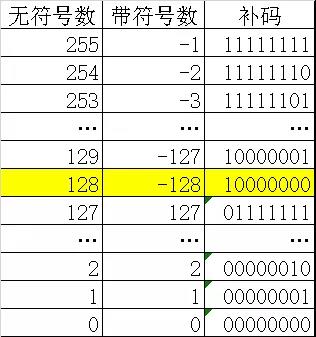
从另外一个角度讲，补码的存在，实现了有符号数和无符号数的一种对应关系，下图的也形象的说明了把1000 0000定为-128的补码合情合理。