687B: Remainders Game

Codeforces Round #360 Editorial [+ Challenges!]


B. Remainders Game
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

Today Pari and Arya are playing a game called Remainders.

Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 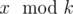. There are n ancient numbers c1, c2, ..., cn and Pari has to tell Arya 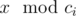if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value 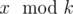for any positive integer x?

Note, that 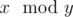means the remainder of x after dividing it by y.

Input

The first line of the input contains two integers n and k (1 ≤ n,  k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.

The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 1 000 000).

Output

Print "Yes" (without quotes) if Arya has a winning strategy independent of value of x, or "No" (without quotes) otherwise.

Examples
Input
4 5
2 3 5 12
Output
Yes
Input
2 7
2 3
Output
No
Note

In the first sample, Arya can understand 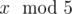because 5 is one of the ancient numbers.

In the second sample, Arya can't be sure what 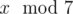is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.




Hint

Assume the answer of a test is No. There must exist a pair of integers x1 and x2 such that both of them have the same remainders after dividing by any ci, but they differ in remainders after dividing by k. Find more facts about x1 and x2!

Solution

Consider the x1 and x2 from the hint part. We have x1 - x2 ≡ 0 (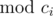) for each 1 ≤ i ≤ n.

So:

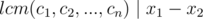
We also have 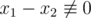(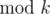). As a result:

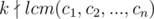
We've found a necessary condition. And I have to tell you it's also sufficient!

Assume 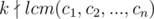, we are going to prove there exists x1, x2 such that x1 - x2 ≡ 0 (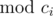) (for each 1 ≤ i ≤ n), and ().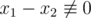

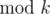A possible solution is x1 = lcm(c1, c2, ..., cn) and x2 = 2 × lcm(c1, c2, ..., cn), so the sufficiency is also proved.

So you have to check if lcm(c1, c2, ..., cn) is divisible by k, which could be done using prime factorization of k and ci values.

For each integer x smaller than MAXC, find it's greatest prime divisor gpdx using sieve of Eratosthenes in .

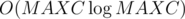Then using gpd array, you can write the value of each coin as p1q1p2q2...pmqm where pi is a prime integer and 1 ≤ qi holds. This could be done in 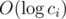by moving from ci to 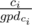and adding gpdci to the answer. And you can factorize k by the same way. Now for every prime p that , see if there exists any coin i that the power of p in the factorization of ci is not smaller than the power of p in the factorization of k.

Complexity is .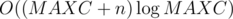


C++ code

//     . .. ... .... ..... be name khoda ..... .... ... .. .     \\

#include <bits/stdc++.h>
using namespace std;

inline int in() { int x; scanf("%d", &x); return x; }
const long long N = 1200021;

int cntP[N], isP[N];

int main()
{
	for(int i = 2; i < N; i++)
		if(!isP[i])
			for(int j = i; j < N; j += i)
				isP[j] = i;
	int n = in(), k = in();
	for(int i = 0; i < n; i++)
	{
		int x = in();
		while(x > 1)
		{
			int p = isP[x];
			int cnt = 0;
			while(x % p == 0)
			{
				cnt++;
				x /= p;
			}
			cntP[p] = max(cntP[p], cnt);
		}
	}
	bool ok = 1;
	while(k > 1)
	{
		ok &= (cntP[isP[k]] > 0);
		cntP[isP[k]]--;
		k /= isP[k];
	}
	cout << (ok ? "Yes\n" : "No\n");
}



原文链接：Codeforces Round #360 Editorial [+ Challenges!] - Codeforces


posted on 2016-07-02 09:03  海岛Blog  阅读(159)  评论(0)    收藏  举报

导航