POJ1609 UVALive2815 UVA1196 ZOJ1787 Tiling Up Blocks【二维最长上升子序列+DP】

Tiling Up Blocks

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5882		Accepted: 2293

Description

Michael The Kid receives an interesting game set from his grandparent as his birthday gift. Inside the game set box, there are n tiling blocks and each block has a form as follows: 

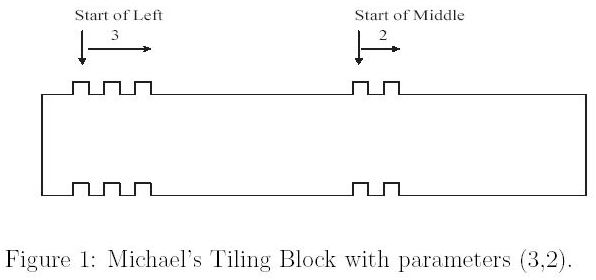
Each tiling block is associated with two parameters (l,m), meaning that the upper face of the block is packed with l protruding knobs on the left and m protruding knobs on the middle. Correspondingly, the bottom face of an (l,m)-block is carved with l caving dens on the left and m dens on the middle. 
It is easily seen that an (l,m)-block can be tiled upon another (l,m)-block. However,this is not the only way for us to tile up the blocks. Actually, an (l,m)-block can be tiled upon another (l',m')-block if and only if l >= l' and m >= m'. 
Now the puzzle that Michael wants to solve is to decide what is the tallest tiling blocks he can make out of the given n blocks within his game box. In other words, you are given a collection of n blocks B = {b1, b2, . . . , bn} and each block bi is associated with two parameters (li,mi). The objective of the problem is to decide the number of tallest tiling blocks made from B. 

Input

Several sets of tiling blocks. The inputs are just a list of integers.For each set of tiling blocks, the first integer n represents the number of blocks within the game box. Following n, there will be n lines specifying parameters of blocks in B; each line contains exactly two integers, representing left and middle parameters of the i-th block, namely, li and mi. In other words, a game box is just a collection of n blocks B = {b1, b2, . . . , bn} and each block bi is associated with two parameters (li,mi). 
Note that n can be as large as 10000 and li and mi are in the range from 1 to 100. 
An integer n = 0 (zero) signifies the end of input.

Output

For each set of tiling blocks B, output the number of the tallest tiling blocks can be made out of B. Output a single star '*' to signify the end of 
outputs.

Sample Input

3
3 2
1 1
2 3
5
4 2
2 4
3 3
1 1
5 5
0

Sample Output

2
3
*

Source

Asia Kaohsiung 2003

Regionals 2003 >> Asia - Kaohsiung

问题链接：POJ1609 UVALive2815 UVA1196 ZOJ1787 Tiling Up Blocks。

题意简述：

若干个积木，每个积木上面有凸起，下面有凹进去的部分。左边凸起与凹进去的个数是一样的，记为L；中间凸起与凹进去的个数也是一样的，记为M。
对应的两个金木能堆起来，当且仅当L1>=L2并且M1>=M2，问最多能堆多高？

问题分析：这是一个二维DP问题。递推式为：dp[i][j] = max(dp[i-1][j],dp[i][j-1])+cnt[i][j]。

程序说明：（略）

AC的C++语言程序如下：

/* POJ1609 UVALive2815 UVA1196 ZOJ1787 Tiling Up Blocks */

#include <iostream>
#include <stdio.h>
#include <string.h>

using namespace std;

const int N = 100;
int cnt[N+1][N+1], dp[N+1][N+1];

int main()
{
    int n, left, mid;

    while(scanf("%d", &n) != EOF && n) {
        memset(cnt, 0, sizeof(cnt));
        memset(dp, 0, sizeof(dp));

        for(int i=0; i<n; i++) {
            scanf("%d%d", &left, &mid);
            cnt[left][mid]++;
        }

        // DP计算过程
        for(int i=1; i<=N; i++)
            for(int j=1; j<=N; j++)
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) +cnt[i][j];

        printf("%d\n", dp[N][N]);
    }
    printf("*\n");

    return 0;
}