【数据结构-02】树状数组
1.引言
树状数组是一种非常好用的东西，主要锻炼lowbit。
以前学完了之后做了一个简单的整理，但远远不够。
所以，我来做这篇博客，希望对大家有帮助。
2.问题
题目描述
如题，已知一个数列，你需要进行下面两种操作：
将某一个数加上 \(x\)
求出某区间每一个数的和
输入格式
第一行包含两个正整数 \(n,m\)，分别表示该数列数字的个数和操作的总个数。
第二行包含 \(n\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。
接下来 \(m\) 行每行包含 \(3\) 个整数，表示一个操作，具体如下：
1 x k含义：将第 \(x\) 个数加上 \(k\)
2 x y含义：输出区间 \([x,y]\) 内每个数的和输出格式
输出包含若干行整数，即为所有操作 \(2\) 的结果。
看到这题我们可以使用暴力算法，模拟所有操作，显然会超时。
接下来，我们就需要请我们的主角上场——树状数组。
3.树状数组
一、定义
我们定义数组\(C_i\)表示树状数组，就拿8个数举例（假设原数组是\(A_i\)）：
- \(C_1=A_1\)
- \(C_2=A_1+A_2\)
- \(C_3=A_3\)
- \(C_4=A_1+A_2+A_3+A_4\)
- \(C_5=A_5\)
- \(C_6=A_5+A_6\)
- \(C_7=A_7\)
- \(C_8=A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8\)
就像这张图，呈现出了一个斜着的树形结构，所以叫做树状数组。
而这些有什么规律呢？我们来看看二进制。
\(1_{10}=1_2\)
\(2_{10}=10_2\)
\(3_{10}=11_2\)
\(4_{10}=100_2\)
\(5_{10}=101_2\)
\(6_{10}=110_2\)
\(7_{10}=111_2\)
\(8_{10}=1000_2\)
很快我们就会找到规律：我们设\(k\)为\(i\)二进制末尾0的个数，那么\(C_i\)就是从自己开始算，往前总共加\(2^k\)位。
可是，计算机不可能像我们一样化成二进制，数0的个数，然后算答案呀！所以，我们找到了另一种方法：\(\text{lowbit(i)=i and -i}\)。
我们可以用6试一下：-6（6的补码）的二进制是010，和6的二进制110按位与，得到10，就是2。而我们发现\(C_6\)就是正好加了总计2位。所以，\(C\)数组的值就很好得到：
for i 1→n:
C[i]=0
for j (i-lowbit(i)+1)→i:
C[i]+=A[i]
以后伪代码中的lowbit(i)均表示\(i\ \text{and -}i\)，看着更方便。
二、单点修改
比如说上面那张图，如果我们要修改\(A_1\)，让他加10，都要变哪些地方？我们来看看。
首先，对应的\(C_1\)需要改变。
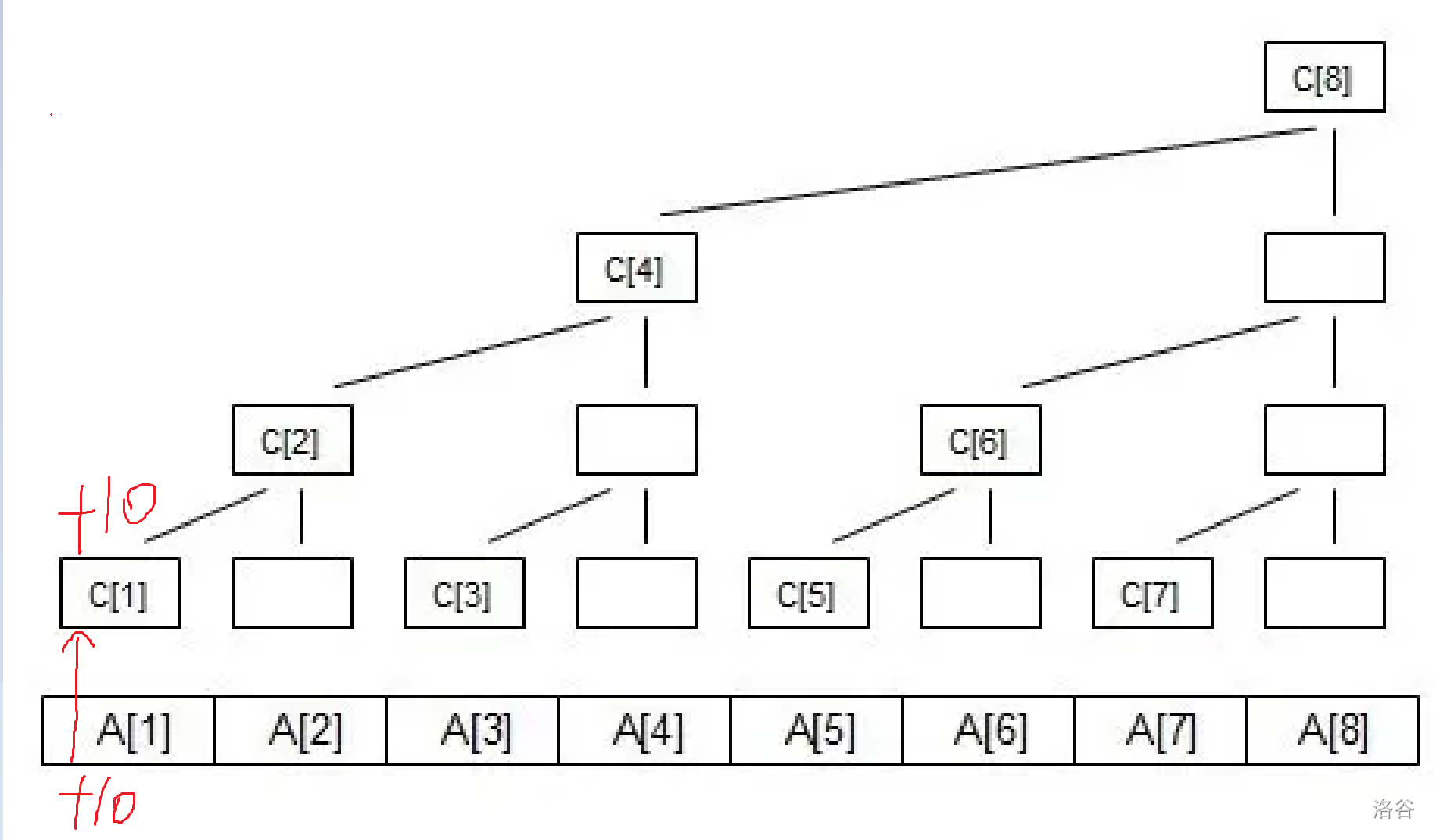
接着，含有\(A_1\)的还有\(C_2,C_4,C_8\)。
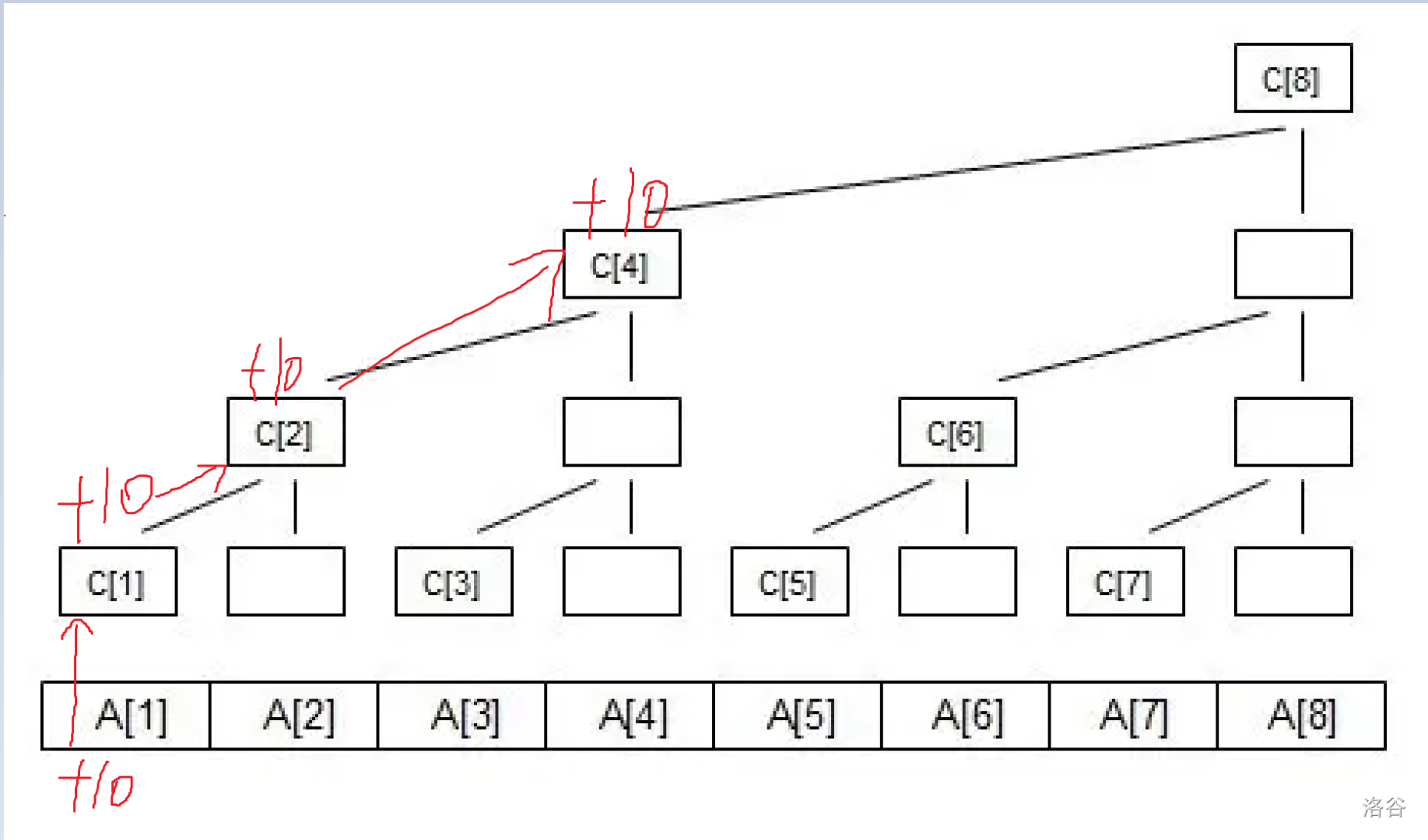
读者可以自行拿2,3,4,5,6,7试试，最终发现每次在\(x\)位置修改，那么下一个要修改的点在\(x+\text{lowbit(x)}\)。所以，我们可以写出伪代码：
add(x,k): 在x这里+k
while x<=n: 只要后面还有(最后一定会到一个超过n的错误位置)
C[x]+=k 我们就把当前的C修改
x+=lowbit(x) 去下一个位置
我们完成了第一个操作，接下来就要思考求和了。
三、区间查询
我们发现，比如7减去\(\text{lowbit(7)}\)得到6，然后减去\(\text{lowbit(6)}\)得到4，然后得到0。而这几个对应的\(C_i\)相加就包含了1到7所有\(A_i\)。所以，我们可以使用一个类似前缀和的思想，计算出结果。
也就是说，我们一直用当前数减去\(\text{lowbit(它本身)}\)，所有经过的C都加上，就能得到答案。
sum(x):
ans=0
while x>0:
ans+=C[x]
x-=lowbit(x)
这时，对于每一组询问\([x,y]\)的结果都必然是\(\text{sum(x)-sum(y-1)}\).
4.代码
整理完所有伪代码，最后给出这道题答案。
#include<iostream>
using namespace std;
int n,m;
int c[500005];//C数组
int a[500005];//A数组
int lbt（int x){//lowbit
return x&(-x);//注意-x要加括号
}
void query(){//初始化
for(int i=1;i<=n;i++){
for(int j=i-lbt(i)+1;j<=i;j++) c[i]+=a[j];
}
void add(int x,int k){//单点修改
for(imt i=x;i<=n;i+=lbt(i)) c[i]+=k;
}
int sum(int x){//区间查询
int ans=0;
for(int i=x;i;i-=lbt(i)) ans+=C[i];
return ans;
}
int main(){
int op,x,y;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
query();
for(int i=1;i<=m;i++){
cin>>op>>x>>y;
if(op==1) add(x,y);//修改
else cout<<sum(y)-sum(x-1)<<endl;//查询
}
return 0;
}
