最大流

某位朋友催更，于是写这篇文章
今天我们讲最大流。

〇、题目＆模型

Link
题目的意思就是说从自来水厂到你家要发水，要经过各个站点，而每一条有向边上都有容量，表示从边那头总共最多发这么多的容量。

一、思路（dinic）

可惜我只会dinic......
首先，如果自来水厂不发水，那肯定是可以的一种方案，叫做零流。
接下来，交了两倍水费的你打开了水龙头，于是自来水厂开始疯狂运水。
就拿这张图：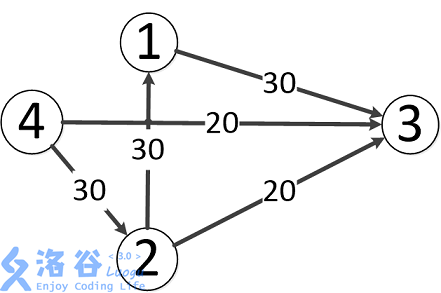
其中4是源点，3是汇点。

1.犯难的水

自来水厂把水发了出去，此时，水为难了。他可以走2也可以走3，走哪个呢？
自来水厂不想多考虑，选择：“走编号小的那个！”
在我们看来，其实他是一个DFS，走完小的走大的。不过，我们走完之后就让我们走的路容量减去我们流量。如果流量超过了容量，就只走容量那么多。
于是，水选择4->2->1->3，30流量。
1无路可走，退回2。
2没有流量了，退回4。
一直到这时，4才走到3，20流量。
总共走到了50流量。
用巨佬的话来讲：

2.犯错的水

那么，接下来是一个最最最最最经典的最大流图片了：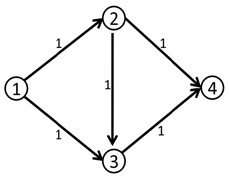
我们第一次找到了1->2->3->4这条增广路，这条路上的流量值显然是1。
于是我们修改后得到了下面这个流。（图中的数字是剩余容量）

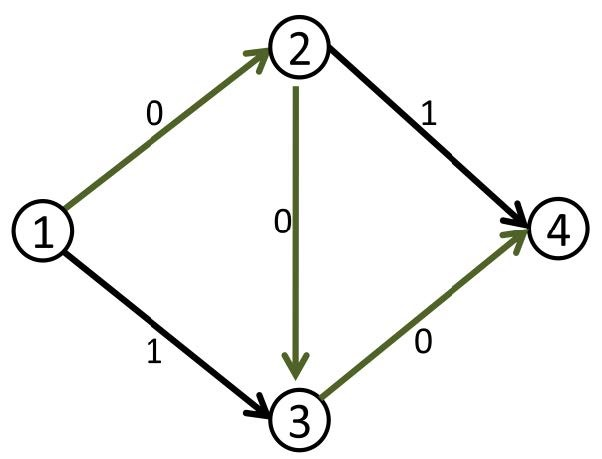
这时候1,2和3,4边上的容量都用完了，我们再也找不到其他的路了，当前的流量是1。
但是，这个答案明显不是最大流，因为我们可以同时走1->2->4和1->3->4，这样可以得到流量为2的流。
问题就出在我们没有给他一个撤销的机会。
因此，我们……加反向边！
输入时，把每一条边都加上反向边，容量相同，就可以“撤销”这一步了（从当前位置回去，流量不变）。

二、代码

照着写的代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,s,t;
struct edge{//一条边
	int from,to,c,f;
	edge(int u,int v,int cc,int ff):from(u),to(v),c(cc),f(ff){}
};
vector<edge> e;
vector<int> G[205];
int d[205],cur[205];
bool vis[205];
void init(int n){//初始化
	for(int i=1;i<=n;i++) G[i].clear();
	e.clear();
}
void add(int from,int to,int ccc){//加边
	e.push_back(edge(from,to,ccc,0));
	e.push_back(edge(to,from,0,0));
	m=e.size();
	G[from].push_back(m-2);
	G[to].push_back(m-1);
}
bool bfs(){//判断是否能走
	memset(vis,0,sizeof(vis));
	queue<int> q;
	q.push(s);
	d[s]=0;
	vis[s]=1;
	while(!q.empty()){
		int x=q.front();
		q.pop();
		for(int i=0;i<G[x].size();i++){//有边可走
			edge& ed=e[G[x][i]];
			if(!vis[ed.to]&&ed.c>ed.f){//能够走到
				vis[ed.to]=1;
				d[ed.to]=d[x]+1;
				q.push(ed.to);
			}
		}
	}
	return vis[t];//还有可行流
}
int DFS(int x,int a){//开始计算
	if(x==t||!a) return a;
	int flow=0,F;
	for(int& i=cur[x];i<G[x].size();i++){
		edge& ee=e[G[x][i]];
		if(d[x]+1==d[ee.to]&&(F=DFS(ee.to,min(a,ee.c-ee.f)))>0){//走边
			ee.f+=F;
			e[G[x][i]^1].f-=F;
			flow+=F;
			a-=F;
			if(a==0) break;
		}
	}
	return flow;
}
signed main(){
	cin>>n>>m>>s>>t;
	int x=m;
	init(n);
	int a,b,ca;
	for(int i=1;i<=x;i++){
		cin>>a>>b>>ca;
		add(a,b,ca);
	}
	int flow=0;
	while(bfs()){//计算最大流
		memset(cur,0,sizeof(cur));
		flow+=DFS(s,0x3f3f3f3f3f3f3f3f);
	}
	cout<<flow<<endl;
	return 0;
}

那么今天就讲到这里，我们下次再见~~~