Rethinking and Improving Relative Position Encoding for Vision Transformer: ViT中的位置编码

Rethinking and Improving Relative Position Encoding for Vision Transformer

* Authors: [[Kan Wu]], [[Houwen Peng]], [[Minghao Chen]], [[Jianlong Fu]], [[Hongyang Chao]]

---

初读印象

comment:: (iRPE)提出了专门用于图像的相对位置编码方法，code:Cream/iRPE at main · microsoft/Cream (github.com)

动机

注意力机制中，输入特征的顺序并不会影响注意力计算，也就是说注意力操作是对位置不敏感的。nlp中常用1维位置编码，而在图像中需要提出二维的位置编码。

• 绝对位置编码：每个位置都有一个单独的编码向量。
• 相对位置编码：用两个位置之间的关系在查找表之中得到对应的编码向量。

方法

• 创新点：
  • 为了研究编码是否可以独立于输入嵌入，引入两种相对位置模式：偏置和上下文。
  • 引入分段函数以进行位置编码。

统一公式

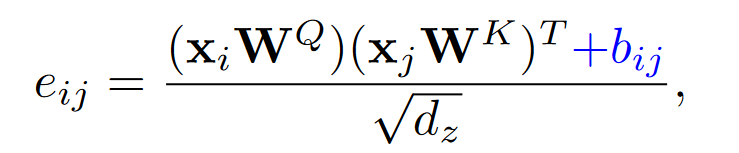其中\(e_{ij}\)是query_i和key_j之间的相关性，\(b_{ij}\)是二维相对位置编码。* 偏执模式：

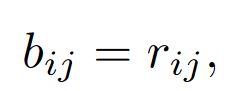
\(r_{ij}\)是一个可学习的标量

• 上下文模式：

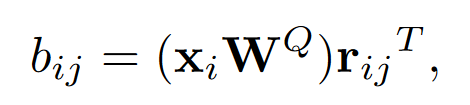或

或
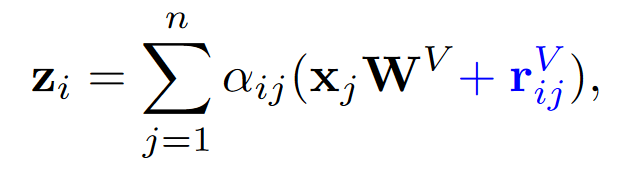\(r_{ij}\)是可学习的向量。

分段指标函数(Piecewise Index Function)

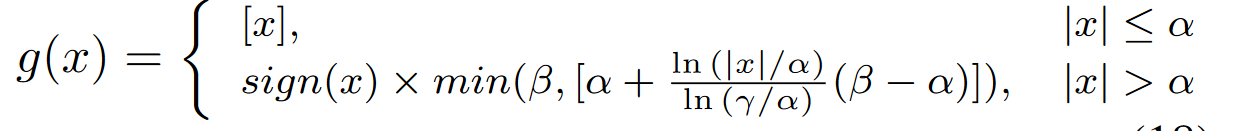
其中[·]代表四舍五入；sign(x)中x大于0为1，小于0为-1，等于0为0；\(\alpha\)是分界点；\(\beta\)控制输出区间，\(\gamma\)控制对数部分的曲率。

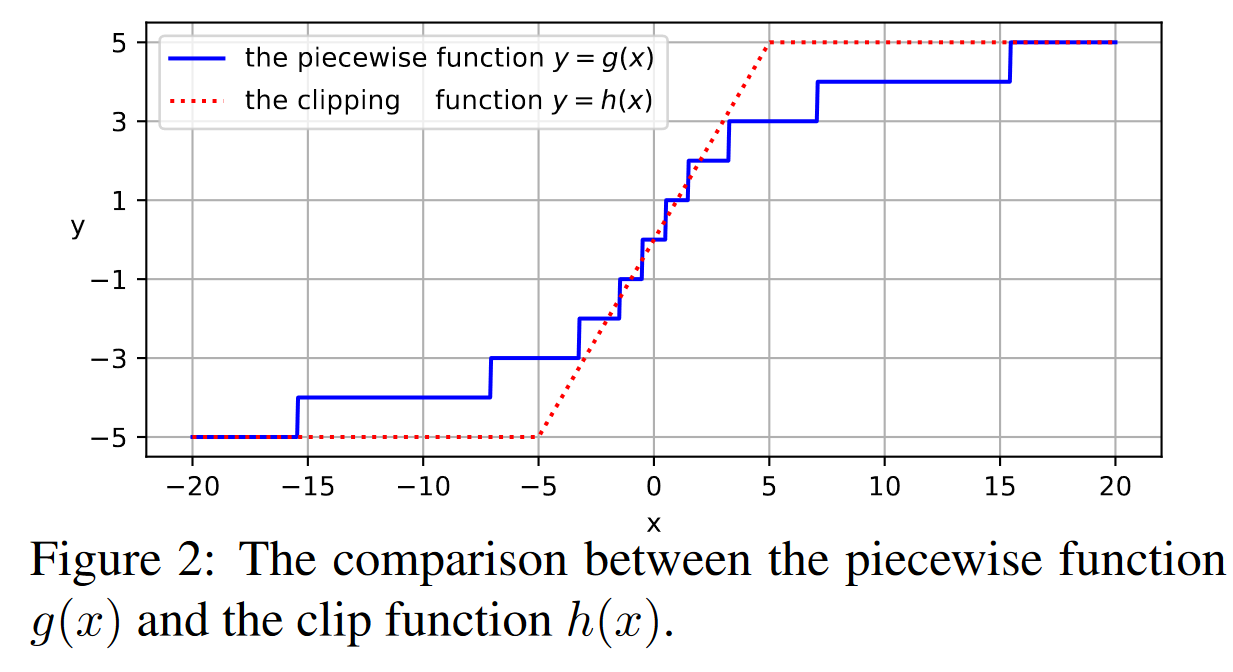
能够通过相对距离分配不同级别的注意力。

2D相对位置计算

Euclidean method

是一种无向的方法。
计算两个点之间的欧式距离并将其投影到对应编码空间。
偏置\(r_{ij}\)为

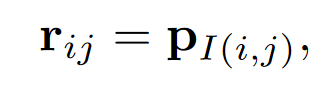
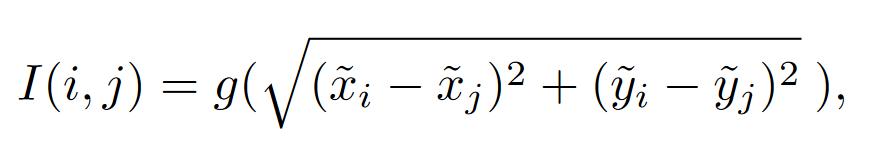
\(P_{I(i,j)}\)表示将\(I{(i,j)}\)投影到可学习的标量或者向量上。将\(P_{I(i,j)}\)看作一个桶，用于存储相对位置权重。桶的数量为\(2\beta + 1\)。

Quantization method

是一种无向的方法。
欧氏距离在临近点时会被映射到同一个距离，如相对距离(1,0)=1和(1,1)=1.41都会被四舍五入成1，所以多加一个quant映射如下
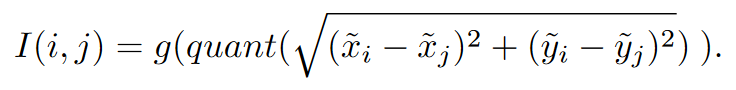其中

Cross method

是一种有向的方法，分别在水平方向和垂直方向上编码，然后将他们相加：
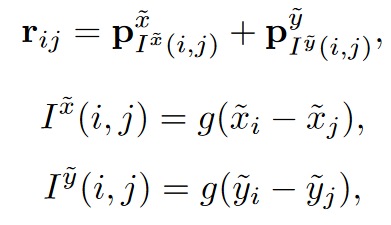其中\(p^\hat{x}\)和\(p^\hat{y}\)都是可学习的标量或向量，桶的数量为\(2\times(2\beta+1)\)。

Product Method

有向方法，使用二维编码

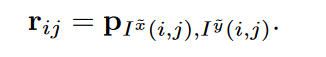
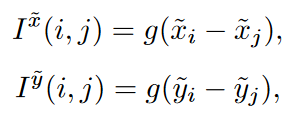其中\(P_{I^\hat{x}(i,j),I^\hat{y}(i,j)}\)为可学习的标量或向量，桶的数量为\((2\beta+1)^2\)。### 表现
有向强于无向，语义强于偏置。

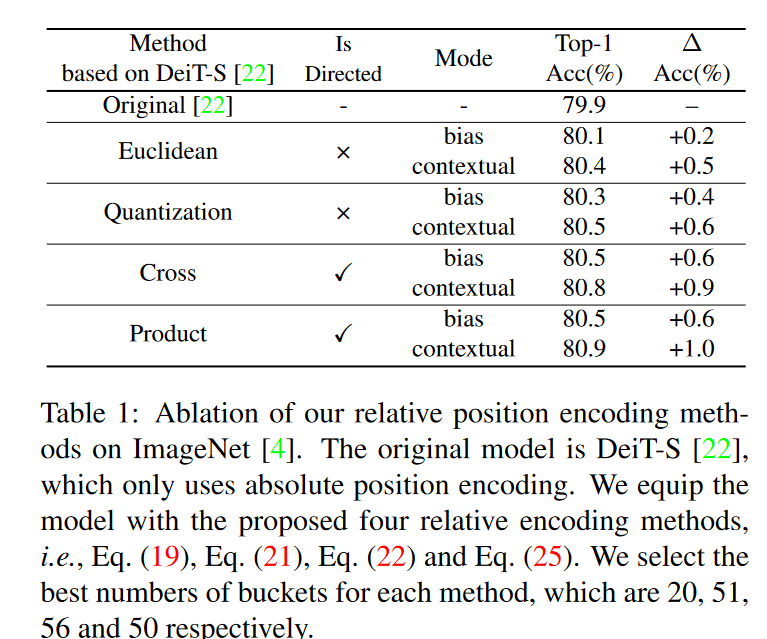
启发

用可学习的参数来代替人工设置的位置编码，拥有更好的学习效果，而且实现起来也更简单。