InternImage: Exploring Large-Scale Vision Foundation Models with Deformable Convolutions 可变形卷积v3
InternImage: Exploring Large-Scale Vision Foundation Models with Deformable Convolutions
* Authors: [[Wenhai Wang]], [[Jifeng Dai]], [[Zhe Chen]], [[Zhenhang Huang]], [[Zhiqi Li]], [[Xizhou Zhu]], [[Xiaowei Hu]], [[Tong Lu]], [[Lewei Lu]], [[Hongsheng Li]], [[Xiaogang Wang]], [[Yu Qiao]]
初读印象
comment:: (InterImage)提出了一种新的基于卷积神经网络的大规模基础模型,该模型可以从增加参数和ViTs等训练数据中获得增益。以可变形卷积为核心算子,使模型不仅具有检测、分割等下游任务所需的大的有效感受野,还具有受输入和任务信息限制的自适应空间聚合。
动机
ViT是大模型的首选,但是本文认为CNN有不输于ViT的潜力。
ViT和CNN的不同之处:
- 从算子层面来看,ViTs的多头自注意力( MHSA )具有长程依赖性和自适应空间聚集性,得益于灵活的MHSA,ViTs可以从海量数据中学习到比CNNs更强大和鲁棒的表示。
- 除了MHSA之外,ViTs还包含了一系列标准CNNs不包含的高级组件,如层归一化( LN ) 、前馈网络( FFN ) 、GELU等。
- 与MHSA的权重由输入动态调节相比,正则卷积是一种具有静态权重和强归纳偏差(如2D局部性、邻域结构、平移等价性等)的算子。由于具有高度归纳性,由规则卷积组成的模型可能比ViTs收敛更快,需要更少的训练数据,但这也限制了CNNs从网络规模数据中学习更一般和更鲁棒的模式。
四种不同的聚合方式:
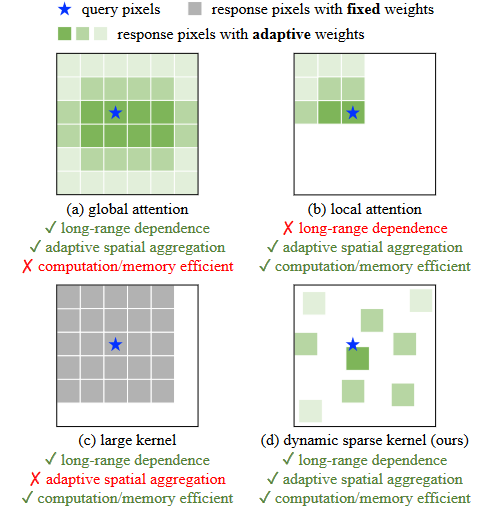
( a )展示了多头自注意力( MHSA )的全局聚集性,其计算和内存成本在需要高分辨率输入的下游任务中昂贵。
( b )将MHSA的范围限制在局部窗口内,以降低成本。
( c )是一个具有非常大的核的深度卷积来建模长程依赖。
( d )是一个可变形卷积,它具有与MHSA相似的良好性质,并且对于大规模模型足够有效。我们从它入手,构建一个大规模的CNN。
为了克服其他三种方法的缺点,设计了一个公共窗口大小为3 × 3的动态稀疏卷积:
- 其采样偏移量可以灵活地从给定数据中动态地学习合适的感受野(可以是长程的,也可以是短程的);
- 根据输入数据自适应地调整采样偏移量和调制标量,可以像ViTs一样实现自适应空间聚合,降低了常规卷积的过感性偏差;
- 卷积窗口为常见的3 × 3,避免了大稠密核带来的优化问题和昂贵的成本。
方法
弥补卷积和MHSA之间的鸿沟的方法是引入长程依赖和自适应空间聚合。
DCN_v2

- 偏移量\(\Delta p_k\)带来了灵活的短程或长程依赖。
- 偏移量\(\Delta p_k\)和调制标量\(m_k\)是可学习的,也就是课自适应空间聚合的。
改进v3
归纳
- 卷积神经元之间共享权重:与正则卷积类似,原始DCNv2中不同的卷积神经元1具有独立的线性投影权重,因此其参数和记忆复杂度与采样点总数呈线性关系,这显著限制了模型的效率,尤其是在大规模模型中。为了解决这个问题,本文借鉴可分离卷积的思想,将原始的卷积权重\(w_k\)分解为深度和点两个部分,其中深度部分由原始的位置感知调制标量\(m_k\)负责,点部分为采样点之间共享的投影权重\(w\)。结合下文公式,我对\(w\)的理解是它是对于位置\(k\)无关的,对卷积中的所有点做了相同的通道上的映射;而\(m_k\)则是对通道无关的,它对一个点的所有通道有着相同的权重,并以该权重来将其聚合到卷积核中。
- 引入Multi - Group机制:多群(头)设计最早出现在群卷积中,被广泛应用于变压器的MHSA中,通过自适应空间聚合,有效地从不同位置的不同表示子空间中学习更丰富的信息。受此启发,本文将空间聚合过程拆分为G个组,每个组具有单独的采样偏移量\(∆p_{gk}\)和调制尺度\(m_{gk}\),因此单个卷积层上的不同组可以具有不同的空间聚合模式,从而为下游任务提供更强的特征。
- 沿采样点归一化调制标量:原始DCNv2中的调制标量采用sigmoid函数进行逐元素归一化。因此,每个调制标量都在范围内,所有样本点的调制标量之和并不稳定,在0 ~ K之间变化,这导致在使用大规模参数和数据进行训练时,DCNv2层中的梯度不稳定。为了缓解不稳定问题,本文将沿样本点的逐元素sigmoid归一化改为softmax归一化。这样,调制标量之和被约束为1,使得不同尺度下模型的训练过程更加稳定。
具体
对于目标点\(p_0\):
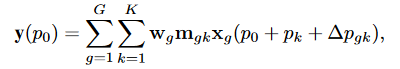
式中:\(G\)表示聚集群数。对于第\(g\)组,\(w_g∈R^{C × C′}\),\(m_{gk}∈R\)表示该组与位置无关的投影权值,其中\(C′= C / G\)表示组维度;\(m_{gk}∈R\)表示第\(g\)组第\(k\)个采样点的调制标量,沿维度\(K\)用softmax函数归一化;\(xg∈R^{C′× H × W}\)表示切片输入特征图;\(∆p_{gk}\)为第\(g\)组网格采样位置\(p_k\)对应的偏移量。
优点
- 该算子弥补了正则卷积在长距离依赖和自适应空间聚合方面的不足;
- 与常见的MHSA和紧密相关的可变形注意力等基于注意力的算子相比,该算子继承了卷积的归纳偏向性,使得模型具有更少的训练数据和更短的训练时间;
- 该算子基于稀疏采样,比之前的方法如MHSA和重新参数化大核等具有更高的计算和内存效率。
InternImage Model
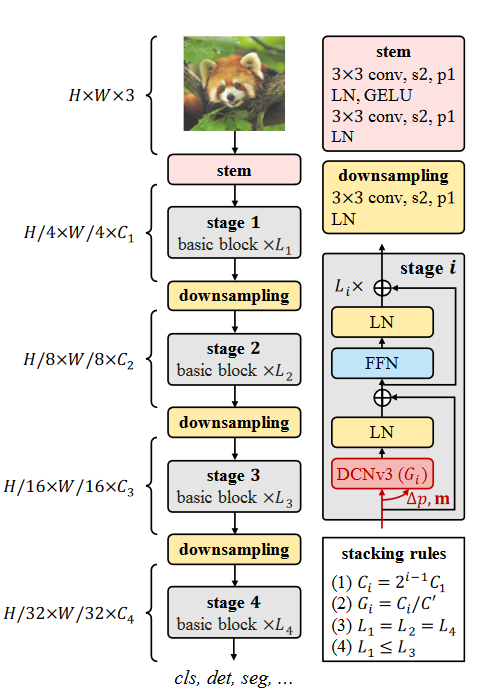
- 基础块:使用LN,前馈网络FFN,GELU。
- stem和下采样:使用卷积主干和下采样层将特征图调整到不同的尺度。在第一级之前放置主干层,将输入分辨率降低4倍。它由2个卷积、2个LN层和1个GELU层组成,其中2个卷积的核大小为3,步长为2,padding为1,第一个卷积的输出通道为第二个卷积的一半。类似地,下采样层由步幅为2的3 × 3卷积和1的填充组成,后接一个LN层。它位于两个阶段之间,用于对输入特征图进行2倍下采样。
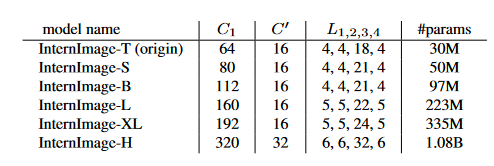
- 堆叠规则:使用上图所示的stacking rules,其中Ci为第i层的通道数;Gi为第i阶段DCNv3的组数;Li为第i阶段的基本块个数。
 ###消融实验
###消融实验
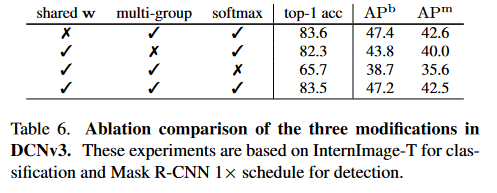
- 卷积神经元之间共享权重很重要。
- 多组空间聚合能够进一步增强特征表示。
启发
可变形卷积中的权重共享和卷积的多头策略可以借鉴到自己的网络中。
对调制变量使用softmax,在我的实验中确实可以帮助模型收敛,但是当堆叠了太多DCN时,还是会导致模型难以收敛,或许是因为本文参考了ViT的基本块设计,在DCN前后加入残差,使得模型更好地收敛?


