GCGP:Global Context and Geometric Priors for Effective Non-Local Self-Attention加入了上下文信息和几何先验的注意力
Global Context and Geometric Priors for Effective Non-Local Self-Attention
* Authors: [[Woo S]]
初读印象
comment:: (GCGP)提出了一个新的关系推理模块,它包含了一个上下文化的对角矩阵和二维相对位置表示。
动机
普通注意力的缺点:
- 单独处理输入图像中的每个特征,并在整个输入中执行注意力。因此,在计算元素之间的关系时没有考虑上下文信息。
- 位置信息的表示是缺失的,因此不能很好地利用图像中固有的空间相关性。(注意力是没有计算顺序的,特征向量变换位置对它来说完全没有影响)
方法
普通注意力
输入:
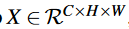
经过三个1×1卷积: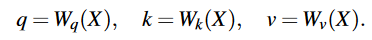
输出特征维度为\(\hat{C}\)
计算亲和力矩阵\(A\in N\times \hat{N},N=H\times W\):
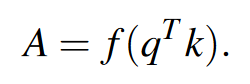
得到最终输出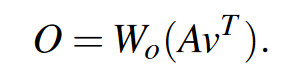
上下文先验
在注意力计算中融入对角线上下文矩阵\(c\in \hat{C}\times \hat{C}\):
 其中c为:
其中c为: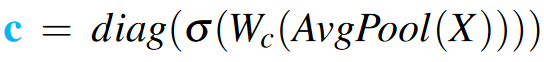
即对X做全局平均池化、1×1卷积(\(C\to \hat{C}\))、sigmoid,并将其放到矩阵的对角线上。
\(q^T c\)相当于加强\(q^T\)上对应通道的点并屏蔽其他点,其实相当于\(q^T\)的每一行乘没有对角化之前的c。
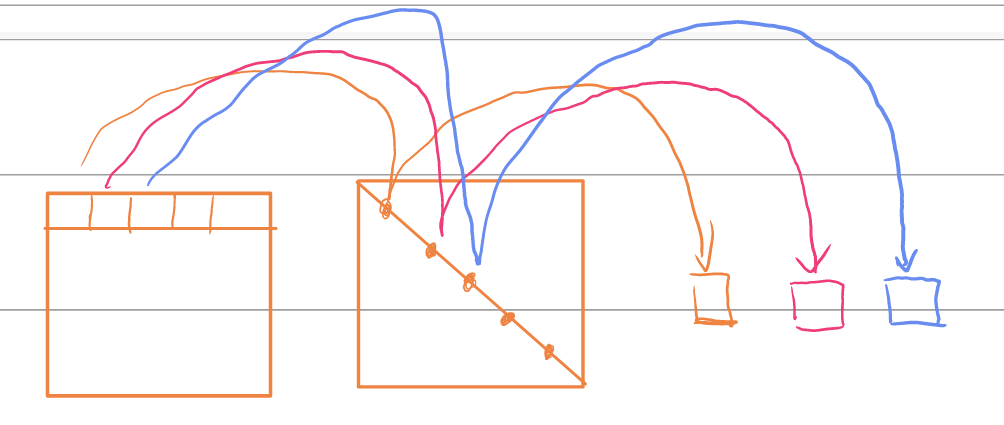
几何先验
在亲和力矩阵计算的过程中加入相对位置先验r:
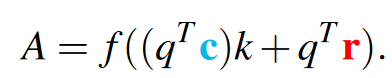
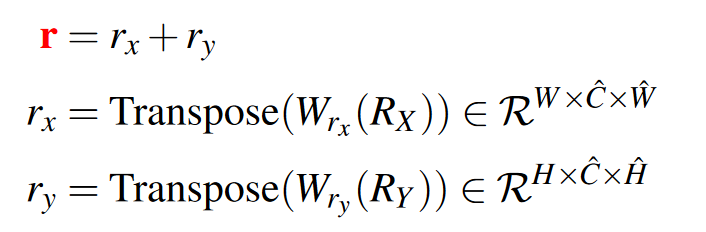
其中\(R_X\in \frac{C}{2}\times W\times \hat{W},R_Y \in \frac{C}{2}\times H\times\hat{H}\),它们是一维的相对位置信息。W是输出通道为\(\hat{C}\)的1×1卷积,Transpose是将第0维和第1维调换。
\(R_{X,i,j}\)是\(R_X\)中第i行第j列的向量,其中每个元素的计算方法如下:
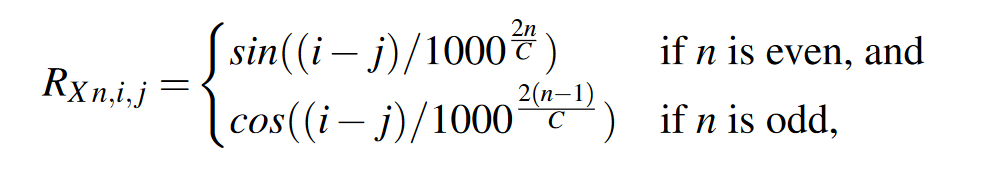 其中
其中
在一维相对位置信息的计算中,i和j是固定的,(i-j)决定了余弦和正弦函数的计算范围,分母意味在这段范围内的函数中以固定比例采样,那么同一个(i-j),只能采样出一个独一无二的向量。
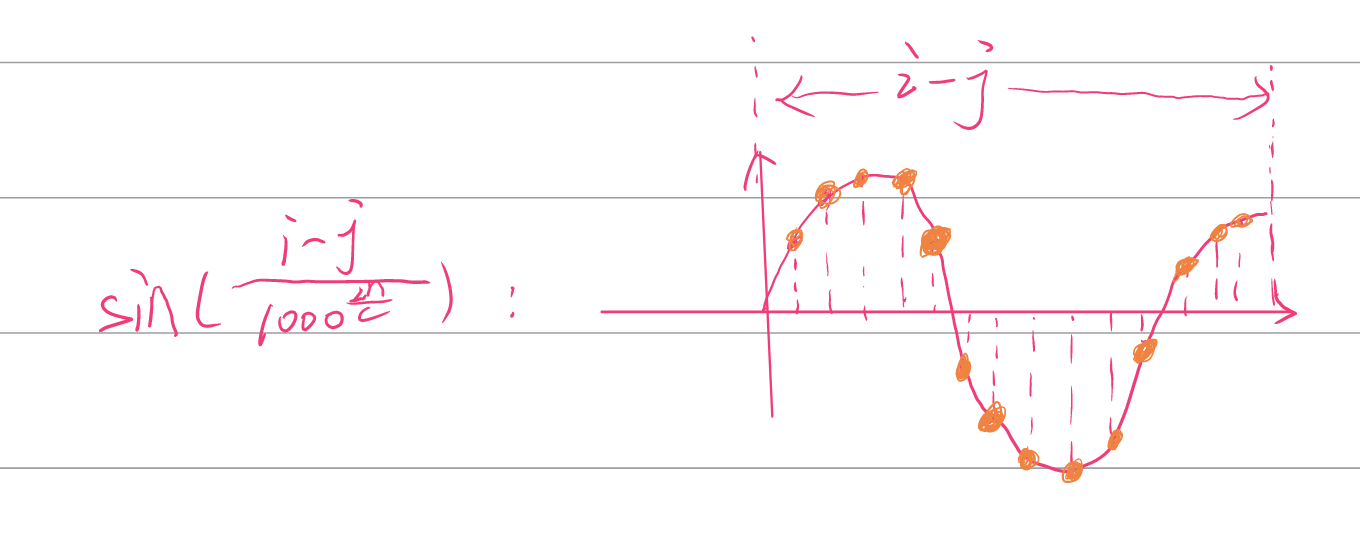
最后计算2D相对位置信息
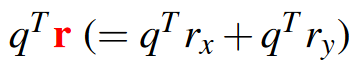 先将\(q^T\)reshape成\(W\timesH\times \hat{C}\),然后取出后面两维与\(r_x\)相乘:
先将\(q^T\)reshape成\(W\timesH\times \hat{C}\),然后取出后面两维与\(r_x\)相乘:
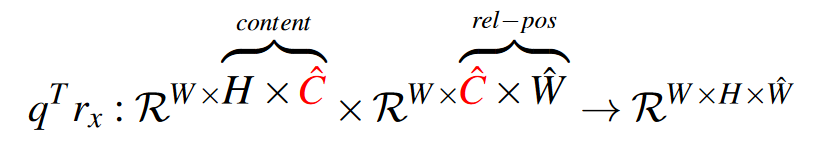

\(r_y\)同理:
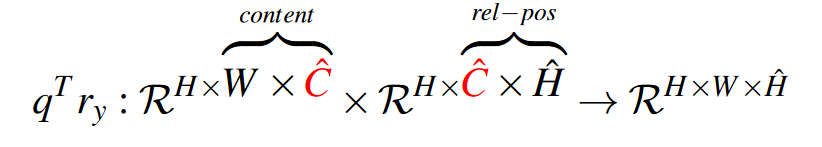 \(q^Tr_x\)和\(q^Tr_y\)以广播的形式相加最后一维,得到\(q^Tr\inH\times W\times \hat{H}\times \hat{W}\)也就是\(N\times \hat{N}\)。
\(q^Tr_x\)和\(q^Tr_y\)以广播的形式相加最后一维,得到\(q^Tr\inH\times W\times \hat{H}\times \hat{W}\)也就是\(N\times \hat{N}\)。
整体架构
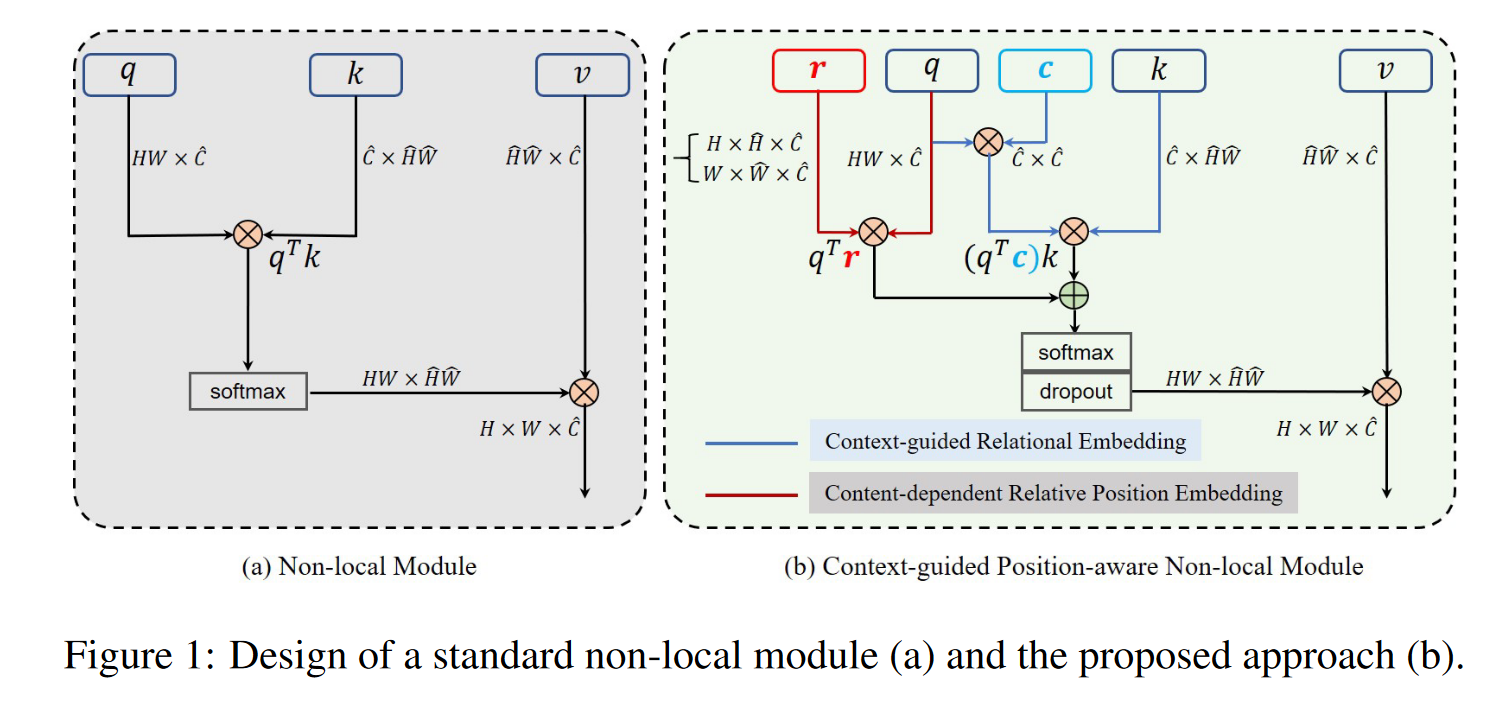
其他
使用了多头注意力和对亲和力矩阵使用了dropout。
表现
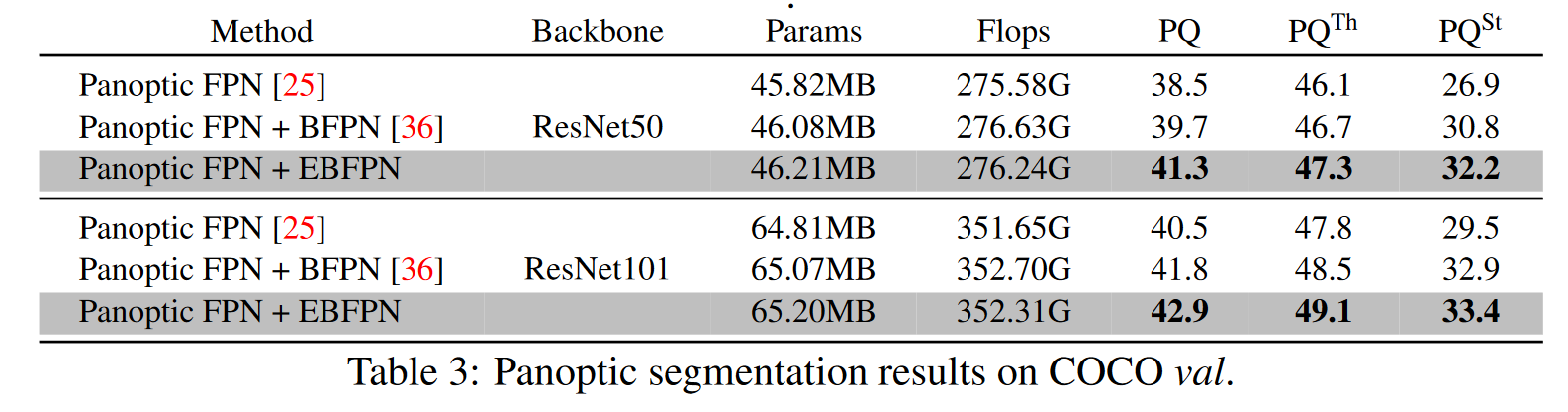
局限性
对角线上下文矩阵太暴力了,直接把其他通道的信息给屏蔽了。
位置编码的方式太复杂且可解释性不强。
启示
使用了多头注意力,在注意力中嵌入了相对位置编码。


