Expectation-Maximization Attention Networks for Semantic Segmentation 使用了EM算法的注意力
Expectation-Maximization Attention Networks for Semantic Segmentation
* Authors: [[Xia Li]], [[Zhisheng Zhong]], [[Jianlong Wu]], [[Yibo Yang]], [[Zhouchen Lin]], [[Hong Liu]]
初读印象
comment:: (EMANet)用期望最大化方法计算注意力机制，更加节省计算资源和时间，具有更强的鲁棒性。
Why
卷积难以捕捉长程依赖，注意力计算了所有点之间的依赖，但太消耗计算资源。
What
提出了期望最大化注意力算法Expectation Maximization Attention (EMA)。不在所有像素点上重构，而是用EM算法寻找紧凑的基础集以减少计算量。
How
Expectation-Maximization Algorithm
[[EM算法]]是一种迭代优化策略，由于它的计算方法中每一次迭代都分两步，其中一个为期望步（E步），另一个为极大步（M步），所以算法被称为EM算法（Expectation Maximization Algorithm）。其基本思想是：首先根据己经给出的观测数据，估计出模型参数的值；然后再依据上一步估计出的参数值估计缺失数据的值，再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计，然后反复迭代，直至最后收敛，迭代结束。
- E步:根据先验得到z的分布\(Q(z)=p(Z|X,\\theta)\)。
- M步:根据上一步得到的z的分布更新\(\theta\)。
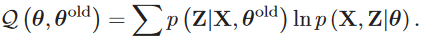
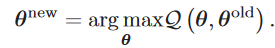
Gaussian Mixture Model
高斯混合分布中有多个不同的高斯分布。在其中得到一个值x的概率为：
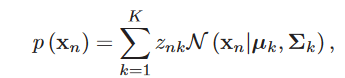其中\(z_{nk}\)表示的是第k个高斯分布所占的比例，\(\Sigma_kz_{nk}=1\)。该模型中需要估算的参数是均值和方差\(\mu_k\)和\(\Sigma_k\)。该模型的似然估计为：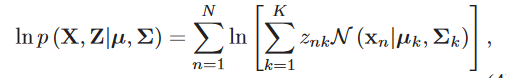
E步：计算Z的分布
M步：用Z更新\(\mu_k\)和\(\Sigma_k\)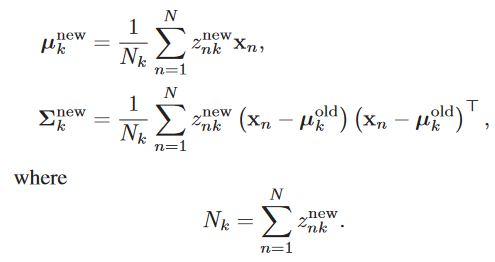
最后从模型中得到的所有高斯函数的均值的均值为
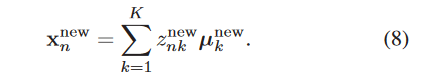####Non-local
[[@Wang2018]]
在Non-local中，从\(x_i\)得到\(y_i\)的注意力机制为：
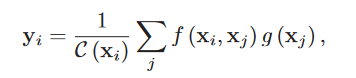
这其实类似于公式8，但他没有经过E步和M步。
Expectation-Maximization Attention
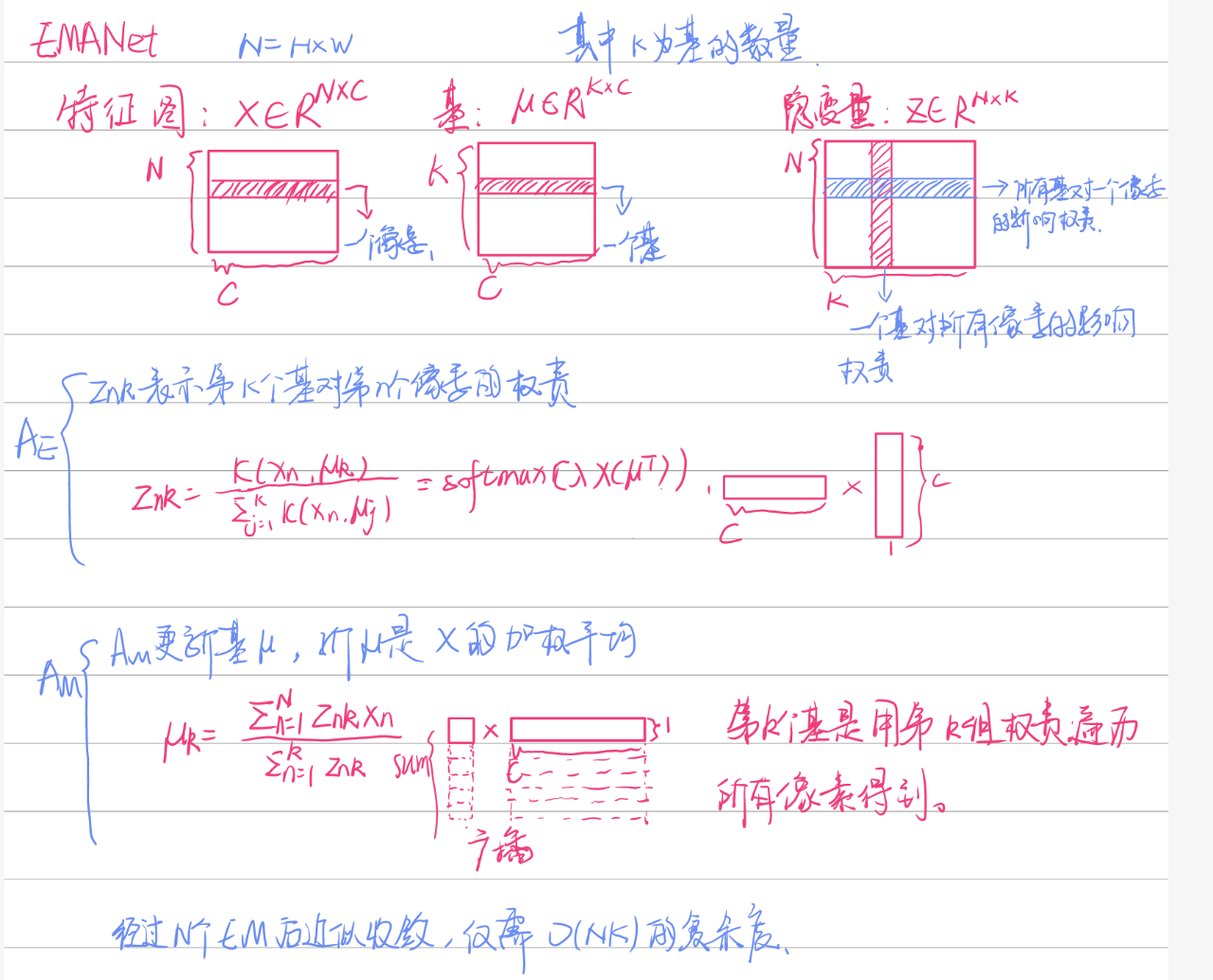
与nonlocal不同的是，nonlocal的基是有N个的，这个复杂度旧比较高。
最后用收敛的Z(N×K)和\(\mu\)(K×C)得到更正后的X(N×C)。
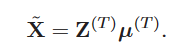####EMA Unit
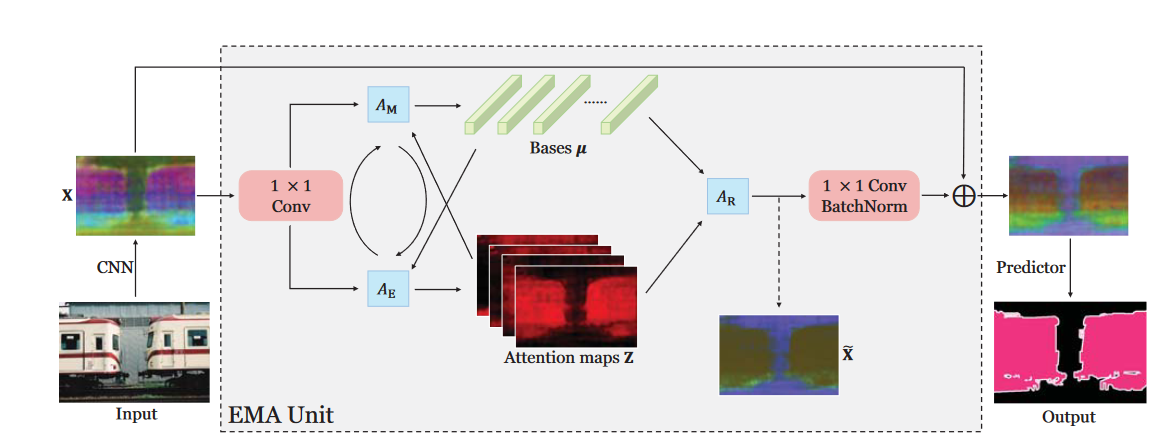
EMA前后有两个1×1卷积，前一个将输入的值域从\(R^+\)映射到\(R\)。
采用Kaiming’s initialization初始化\(\mu^{(0)}\),每张图片有独自的EM计算过程，得到不同的\(\mu^{(T)}\)。
在逐个批次训练的同时，EM参数的迭代初值，\(\mu^{(0)}\)的更新并非采用梯度下降，使用滑动平均更新方式：
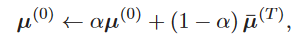
其中\(\hat{\mu}^{(T)}\)为一个小批次中\(\mu^{(T)}\)的平均值。
\(\hat{\mu}^{(t)}\)使用L2noraml
Experiemnt
网络细节
- 主干网络：ResNet
- 学习率策略：Poly
- 初始学习率：0.009
- 动量：0.9
- 权重衰退：0.0001
- 数据增强：随机缩放(0.5-2.0)、裁剪、反转
- 输入尺寸：513×513
消融实验：
\(\mu^{(0)}\)更新方式和正则化
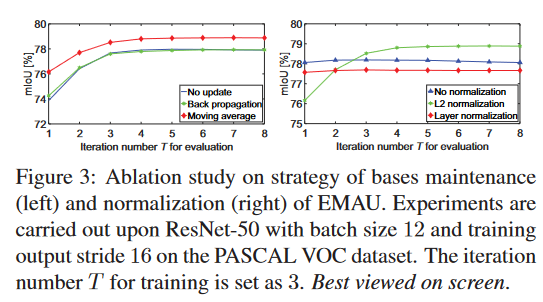EMA使用滑动均值（Movingaverage）和L2Norm最为有效。迭代次数表示EM步数？
迭代次数
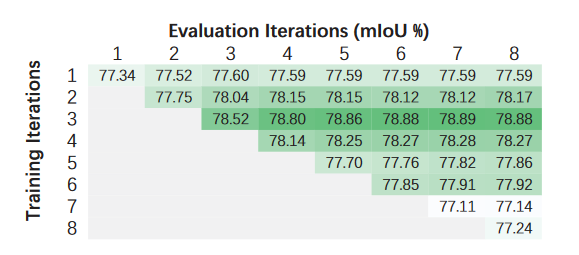
在评估时，每次迭代次数增加都会增加mIOU。但在训练时3次就到顶了。
比较
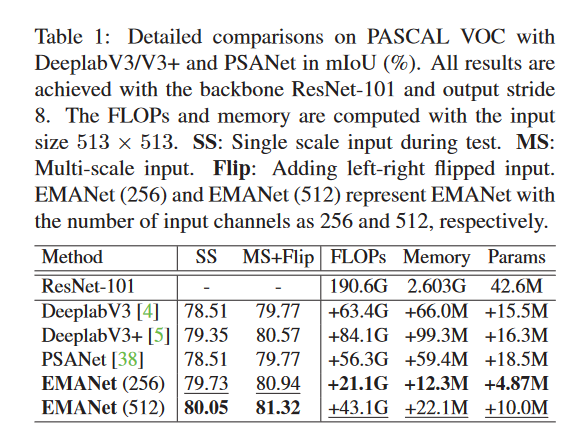EMANet的表现要优于这三个基线的大幅度。此外，EMANet在计算和内存方面要轻得多。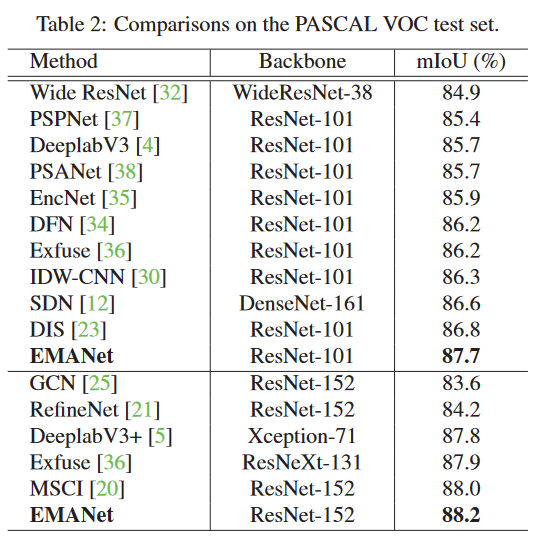
Conclusion
十分优雅的一篇论文，从动机到原理到模型实现都写的有理有据。
Non-Local的基的数量是和像素点的数量是相同的，而EMANet大大减少了基的数量，从而减少了计算量和内存占用，同时注意力模块的更新不是靠梯度下降来的，而是靠滑动平均更新。
