BJOI2019 光线

这段时间一直在刷各省省选题，参考了许许多多的大神的题解，的确收获颇丰。这道题是为数不多的独立推导出正解的题目 窝太蒟了（；´д｀）ゞ 算是涌泉之恩，滴水相报吧

前置芝士：等比数列的通项公式

对于首项为\(a_1\),公比为\(q\)的等比数列，前\(n\)项和\(S_n\)的通项公式如下：

\[ S_n=\left\{ \begin{aligned} \frac{a_1(1-q^n)}{1-q} & (q\not= 1) \\ a_1\times n & (q=1) \end{aligned} \right. \]

证明比较容易，简略思路为将\(q\times S_n -S_n\)的展开推导，这里就交给读者独立完成了

dp推导

令\(f[i]\)为从右向左抵达第\(i\)层玻璃后，能向右返回的百分比

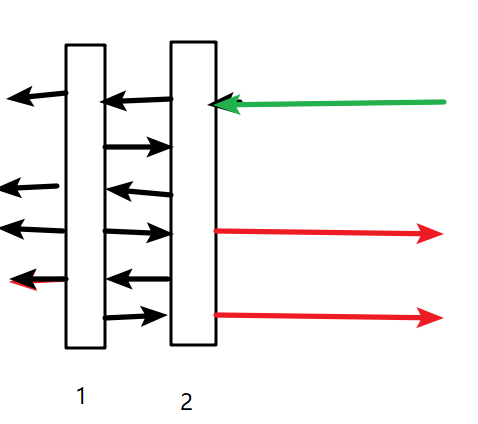
一道绿光
进入第二层玻璃后，黑光会到处反射或穿透，最终回来的红光就是\(f[2]\)所代表的部分

观查得出，红光可以如下分类：直接在第\(i\)层反射的光、在第\(i-1\)层反射了一次后回来的光、在第\(i-1\)层反射了两次后回来的光......

\[\begin{aligned} f[i]=&b[i]\% + a[i]\% \times f[i-1] \times b[i] \% + \\ &a[i]\% \times f[i-1] \times b[i]\% \times f[i-1] \times a[i].. \end{aligned} \]

发现，除第一项外，后面项构成了\(a_1=a[i]\%\times a[i]\%\times f[i-1]\)，\(q=b[i]\%\times f[i-1]\)的等比数列，因此用通项公式加以优化

\[f[i]=b[i]\% + \frac{(a[i]\%)^2\times f[i-1]\times(1-(b[i]\%\times f[i-1])^n))}{1-b[i]\%\times f[i-1]} \]

由于数列有无数项，因此\(f[i]\)递推公式的最终版为：

\[f[i]=b[i]\% + \frac{(a[i]\%)^2\times f[i-1]}{1-b[i]\%\times f[i-1]} \]

令\(g[i]\)为光线到达第\(i\)层玻璃后，能从第\(n\)层射出的部分

还是分情况讨论：直接穿透到下一层、在第\(i-1\)层折回一次后穿透、在第\(i-1\)层折回两次后穿透....

\[\begin{aligned} g[i] = &a[i]\% \times g[i+1] + b[i]\% \times f[i-1] \times a[i]\% \times g[i+1]+ \\ & (b[i]\% \times f[i-1])^2 \times a[i]\% \times g[i+1] ... \end{aligned} \]

同样用等比数列的通项和公式优化

\[g[i]=\frac{a[i]\%\times g[i+1]}{1-b[i]\%\times f[i-1]} \]

至此，我们得到了\(f[]\)和\(g[]\)的通项公式，答案即为\(g[1]\)

#include <bits/stdc++.h>
using namespace std;
#define lor(a,b,c) for(register int a=b;a<=c;++a)
#define ror(a,b,c) for(register int a=c;a>=b;--a)
typedef long long ll;

const int N=5e5+5;
const ll MOD=1e9+7,REV=570000004;

int n; ll a[N],b[N],f[N],g[N];

inline ll qsm(ll x,ll y) {ll ans=1ll; while(y) {if(y&1) (ans*=x)%=MOD; (x*=x)%=MOD; y>>=1;} return ans;}
inline void inc(ll &a,ll b) {(a+=b)>=MOD?a-=MOD:a;}

int main(){
	#ifndef ONLINE_JUDGE
	freopen("test.in","r",stdin);
	#endif

	scanf("%d",&n); lor(i,1,n) scanf("%lld%lld",&a[i],&b[i]);
	f[0]=0ll;
	lor(i,1,n-1){
		f[i]=b[i]*REV%MOD;
		ll t1=a[i]*a[i]%MOD*REV%MOD*REV%MOD*f[i-1]%MOD,t2=1ll,t3=b[i]*REV%MOD*f[i-1]%MOD;;
		inc(t2,MOD-t3); (t1*=qsm(t2,MOD-2))%=MOD; inc(f[i],t1);
	}
	g[n+1]=1ll;
	ror(i,1,n){
		g[i]=a[i]*REV%MOD*g[i+1]%MOD;
		ll t1=1ll,t2=b[i]*REV%MOD*f[i-1]%MOD; inc(t1,MOD-t2); (g[i]*=qsm(t1,MOD-2))%=MOD;
	}
	printf("%lld\n",g[1]);

	return 0;
}