汉诺塔递归过程中参数的变化

汉诺塔问题描述

　　该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。游戏的目标:把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

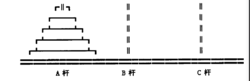
汉诺塔代码实现

#include<stdio.h>

void move(char x,char y)
{
   printf("%c-->%c\n",x,y);
}
//将n个盘从one座借助two座，移到three座
void hanoi(int n,char one,char two,char three)
{
    if(n==1) 
        move(one,three);
    else
    {
        hanoi(n-1,one,three,two);//函数调用完后two和three的参数会发生改变，但下次调用的时候three和two的参数还会再变回来，即two-->B，three-->C(递归内涵：保存本层的堆栈信息和函数入口及形参变量，开始调用下次函数)不理解的话可以看下边的图
        move(one,three);
        hanoi(n-1,two,one,three);
    }
}

int main()
{
  int n;
  printf("input the number of diskes:\n");
  scanf("%d",&n);
  printf("The step to moving %3d diskes:\n",n);
  hanoi(n,'A','B','C');
  return 0;
}

在递归过程中one，two，three这三个参数的变化