关联式容器
AVL tree
为了确保整棵树的深度为O(logN),加了额外的平衡条件“任何结点的左右子树高度相差最多1”。
调整规则:如果某一个子树平衡被打破,那么根据新插入的节点的位置可以分为以下几种:(X是被打破平衡的那个子树的根节点)
- 插入点位于X的左子节点的左子树——左左
- 插入点位于X的左子节点的右子树——左右
- 插入点位于X的右子节点的左子树——右左
- 插入点位于X的右子节点的右子树——右右
1.4为外插可用于单旋;2,3为内插可用于双旋。
RB-tree
另一种被广泛使用的平衡二叉搜索树,也是SGI STL唯一实现的搜寻树,作为关联式容器的底层机制之用。RB-tree的平衡条件虽然不同于AVL-tree(都是二叉搜索树),但同样运用了单旋转和双旋转修正操作。RB-tree的规则:
- 每个节点不是红色就是黑色;
- 根节点为黑色;
- 如果节点为红,其子节点必须为黑;
- 任一节点到NULL(树尾端)的任何路径,所含黑节点数必须相同。
根据规则四:新增节点必须为红色;根据规则三:新增节点的父节点为黑色。
假设新增节点为X,父节点为P,祖父结点为G,伯父结点为S,曾祖父结点为GG;所以新增结点必为叶节点且为红(规则4),若P为红(违反规则3要调整),G必为黑,以下四种考虑
1.S为黑且X为外侧插入,先对PG做一次单旋,在更改PG颜色,即可满足规则3;
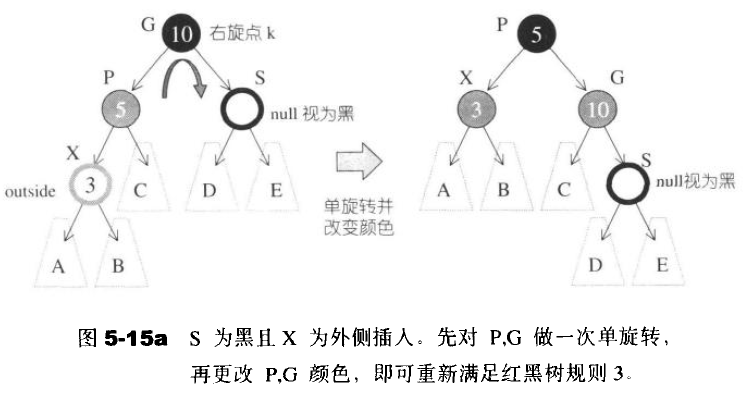
2.S为黑且X为内插,先对PX做一次单旋,更改GX颜色,再对G做单旋,即可满足规则3;

3.S为红且X为外侧插入,先对PG做单旋,并改X颜色,如果此时GG为黑,则结束。

4.S为红且X为外侧插入,先对PG做单旋,并改X颜色,如果此时GG为,继续向上调整直到不再有父子连续为红情况。

RB-tree的结点设计
//RB-tree特有的颜色定义 typedef bool __rb_tree_color_type; const __rb_tree_color_type __rb_tree_red = false; //红色被定义为0 const __rb_tree_color_type __rb_tree_black = true; //黑色被定义为1 //RB-tree节点基本结构 struct __rb_tree_node_base { typedef __rb_tree_color_type color_type; typedef __rb_tree_node_base* base_ptr; color_type color; // 节点颜色,非黑即红 base_ptr parent; // 指向父节点,由于RB-tree时常要上溯其父节点 base_ptr left; // 指向左子节点 base_ptr right; // 指向右子节点 // 一直往左走,就能找到红黑树的最小值节点 // 二叉搜索树的性质 static base_ptr minimum(base_ptr x) { while (x->left != 0) x = x->left; return x; } // 一直往右走,就能找到红黑树的最大值节点 // 二叉搜索树的性质 static base_ptr maximum(base_ptr x) { while (x->right != 0) x = x->right; return x; } }; // 真正的节点定义,采用双层节点结构 // 基类中不包含模板参数 template <class Value> struct __rb_tree_node : public __rb_tree_node_base { typedef __rb_tree_node<Value>* link_type; Value value_field; // 即节点值 };
RB-tree的迭代器

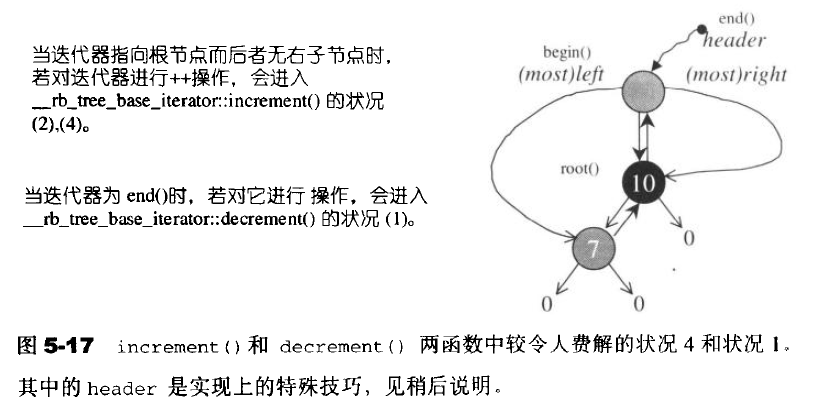
struct __rb_tree_base_iterator { typedef __rb_tree_node_base::base_ptr base_ptr; typedef bidirectional_iterator_tag iterator_category; typedef ptrdiff_t difference_type; base_ptr node; // 用来连接红黑树的节点 // 寻找该节点的后继节点上 void increment() { if (node->right != 0) { // 如果存在右子节点 node = node->right; //【情况1】直接跳到右子节点上 while (node->left != 0) // 然后一直往左子树走,直到左子树为空 node = node->left; } else { // 没有右子节点【情况2】 base_ptr y = node->parent; // 找出父节点 while (node == y->right) { // 如果该节点一直为它的父节点的右子节点 node = y; // 就一直往上找,直到不为右子节点为止 y = y->parent; } if (node->right != y) // 若此时该节点不为它的父节点的右子节点 node = y; // 此时的父节点即为要找的后继节点【情况3】 // 否则此时的node即为要找的后继节点【情况4】 // 我们要寻找根节点的下一个节点,而根节点没有右子节点 // 此种情况需要配合rbtree的header节点的特殊设计,后面会讲到 } } // 寻找该节点你的前置节点 void decrement() { if (node->color == __rb_tree_red && // 如果此节点是红节点 node->parent->parent == node) // 且父节点的父节点等于自己 node = node->right; // 则其右子节点即为其前置节点 // 以上情况发生在node为header时,即node为end()时 // 注意:header的右子节点为mostright,指向整棵树的max节点,后面会有解释 else if (node->left != 0) { // 如果存在左子节点 base_ptr y = node->left; // 跳到左子节点上 while (y->right != 0) // 然后一直往右找,知道右子树为空 y = y->right; node = y; // 则找到前置节点 } else { // 如果该节点不存在左子节点 base_ptr y = node->parent; // 跳到它的父节点上 while (node == y->left) { // 如果它等于它的父子节点的左子节点 node = y; // 则一直往上查 y = y->parent; } // 直到它不为父节点的左子节点未知 node = y; // 此时他的父节点即为要找的前驱节点 } } }; template <class Value, class Ref, class Ptr> struct __rb_tree_iterator : public __rb_tree_base_iterator { //...型别声明 // 迭代器的构造函数 __rb_tree_iterator() {} __rb_tree_iterator(link_type x) { node = x; } __rb_tree_iterator(const iterator& it) { node = it.node; } // 提领和成员访问函数,重载了*和->操作符 reference operator*() const { return link_type(node)->value_field; } pointer operator->() const { return &(operator*()); } // 前置++和后置++ self& operator++() { increment(); return *this; } self operator++(int) { self tmp = *this; increment(); // 直接调用increment函数 return tmp; } // 前置--和后置-- self& operator--() { decrement(); return *this; } self operator--(int) { self tmp = *this; decrement(); // 直接调用decrement函数 return tmp; } };
RB-tree的数据结构
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc> class rb_tree { protected: typedef void* void_pointer; typedef __rb_tree_node_base* base_ptr; typedef __rb_tree_node<Value> rb_tree_node; typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator; // 专属配置器 typedef __rb_tree_color_type color_type; public: // 一些类型声明 typedef Key key_type; typedef Value value_type; typedef value_type* pointer; typedef const value_type* const_pointer; typedef value_type& reference; typedef const value_type& const_reference; typedef rb_tree_node* link_type; typedef size_t size_type; typedef ptrdiff_t difference_type; protected: link_type get_node(){return rb_tree_node_allocator::allocate();} void put_node(link_type p){rb_tree_node_allocator::deallocate(p);} link_type create_node() { link_type tmp=get_node();//配置空间 __STL_TRY { construct(&tmp->value_field,x); } __STL_UNWIND(put_node(tmp)); return tmp; } link_type clone_node(link_type x) { link_type tmp=create_node(x->value_field); tmp->color=x->color; tmp->left=0; tmp->right=0; return tmp; } void destroy_node(link_type p) { destroy(&p->value_field); put_node(p); } protected: // RB-tree的数据结构 size_type node_count; // 记录树的节点个数 link_type header; // header节点设计 Compare key_compare; // 节点间的键值大小比较准则 // 以下三个函数用来取得header的成员 link_type& root() const { return (link_type&) header->parent; } link_type& leftmost() const { return (link_type&) header->left; } link_type& rightmost() const { return (link_type&) header->right; } // 以下六个函数用来取得节点的成员 static link_type& left(link_type x) { return (link_type&)(x->left); } static link_type& right(link_type x) { return (link_type&)(x->right); } static link_type& parent(link_type x) { return (link_type&)(x->parent); } static reference value(link_type x) { return x->value_field; } static const Key& key(link_type x) { return KeyOfValue()(value(x)); } static color_type& color(link_type x) { return (color_type&)(x->color); } // 以下六个函数用来取得节点的成员,由于双层设计,导致这里需要两个定义 static link_type& left(base_ptr x) { return (link_type&)(x->left); } static link_type& right(base_ptr x) { return (link_type&)(x->right); } static link_type& parent(base_ptr x) { return (link_type&)(x->parent); } static reference value(base_ptr x) { return ((link_type)x)->value_field; } static const Key& key(base_ptr x) { return KeyOfValue()(value(link_type(x)));} static color_type& color(base_ptr x) { return (color_type&)(link_type(x)->color); } // 求取极大值和极小值,这里直接调用节点结构的函数极可 static link_type minimum(link_type x) { return (link_type) __rb_tree_node_base::minimum(x); } static link_type maximum(link_type x) { return (link_type) __rb_tree_node_base::maximum(x); } public: // RBTree的迭代器定义 typedef __rb_tree_iterator<value_type, reference, pointer> iterator; private: //... void init() { //构造一个空tree header = get_node(); //产生一个节点空间,令header指向它 color(header) = __rb_tree_red; //令header为红色,用来将 //root与header区分开 root() = 0; leftmost() = header; //header的左子节点为自己 rightmost() = header; //header的右子节点为自己 } public: rb_tree(const Compare& comp=Compare()):node_count(0),key_compare(comp){init();} ~rb_tree() { clear(); put_node(hander); } rb_tree<Key,Value,KeyOfValue,Compare,Alloc>& operator=(const rb_tree<Key,Value,KeyOfValue,Compare,Alloc>& x); public: Compare key_comp() const { return key_compare; } // 由于红黑树自带排序功能,所以必须传入一个比较器函数 iterator begin() { return leftmost(); } // RBTree的起始节点为左边最小值节点 const_iterator begin() const { return leftmost(); } iterator end() { return header; } // RBTree的终止节点为右边最大值节点 const_iterator end() const { return header; } bool empty() const { return node_count == 0; } // 判断红黑树是否为空 size_type size() const { return node_count; } // 获取红黑树的节点个数 size_type max_size() const { return size_type(-1); } // 获取红黑树的最大节点个数,s// 没有容量的概念,故为sizetype最大值 public: pair<iterator,bool> insert_unique(const value_type& x);//保持结点值独一无二 iterator insert_equal(const value_type& x);//允许结点值重复 };
RB-tree的构造与内存管理
RB-tree构造方式有两种,一种是以一个现有的RB-tree复制一个新的RB-tree,另一种是产生一棵空树。
rb_tree<int, int, identity<int>, less<int> > itree; rb_tree(const Compare& comp = Compare()) : node_count(0), key_compare(comp) { init(); } void init() { //构造一个空tree header = get_node(); //产生一个节点空间,令header指向它 color(header) = __rb_tree_red; //令header为红色,用来将 //root与header区分开 root() = 0; leftmost() = header; //header的左子节点为自己 rightmost() = header; //header的右子节点为自己 }
为了控制边界结点,在走到根节点时要特殊处理,为父节点在设计一个根节点hander,在插入结点时不仅要根据RB-tree的特性来维护树,而且还需要hander的正确性,使其父节点指向根节点,左子结点指向最小结点,右子结点指向最大结点。初始状态如下图

RB-tree的元素操作
RB-tree在修正平衡时有三种操作:更改颜色结点,左旋,右旋。在插入时也提供两种操作:insert_unique(插入的键值唯一)、insert_equal(允许插入重复键值)
// 此插入函数不允许重复 // 返回的是一个pair,第一个元素为红黑树的迭代器,指向新增节点 // 第二个元素表示插入操作是否成功的 template<class Key , class Value , class KeyOfValue , class Compare , class Alloc> pair<typename rb_tree<Key , Value , KeyOfValue , Compare , Alloc>::iterator , bool> rb_tree<Key , Value , KeyOfValue , Compare , Alloc>::insert_unique(const Value &v) { rb_tree_node* y = header; // 根节点root的父节点 rb_tree_node* x = root(); // 从根节点开始 bool comp = true; while(x != 0) { y = x; comp = key_compare(KeyOfValue()(v) , key(x)); // v键值小于目前节点之键值? x = comp ? left(x) : right(x); // 遇“大”则往左,遇“小于或等于”则往右 } // 离开while循环之后,y所指即插入点之父节点(此时的它必为叶节点) iterator j = iterator(y); // 令迭代器j指向插入点之父节点y if(comp) // 如果离开while循环时comp为真(表示遇“大”,将插入于左侧) { if(j == begin()) // 如果插入点之父节点为最左节点 return pair<iterator , bool>(_insert(x , y , z) , true);// 调用_insert函数 else // 否则(插入点之父节点不为最左节点) --j; // 调整j,回头准备测试 } if(key_compare(key(j.node) , KeyOfValue()(v) )) // 新键值不与既有节点之键值重复,于是以下执行安插操作 return pair<iterator , bool>(_insert(x , y , z) , true); // 以上,x为新值插入点,y为插入点之父节点,v为新值 // 进行至此,表示新值一定与树中键值重复,那么就不应该插入新值 return pair<iterator , bool>(j , false); } //插入新值:节点键值允许重复 //返回值是一个RB-tree迭代器,指向新增节点 template<class Key , class Value , class KeyOfValue , class Compare , class Alloc> pair<typename rb_tree<Key , Value , KeyOfValue , Compare , Alloc>::iterator , bool> rb_tree<Key , Value , KeyOfValue , Compare , Alloc>::insert_equal(const Value &v) { link_type y = header; link_type x = root(); //从根节点开始 while (x != 0) { //从根节点开始,往下寻找合适的插入点 y = x; x = key_compare(KeyOfValue()(v), key(x)) ? left(x) : right(x); //以上,遇“大”则往左,遇“小于或等于”则往右 } return _insert(x, y, v);// 以上,x为新值插入点,y为插入点之父节点,v为新值 }
无论是哪一种插入方式,最终都需要调用__insert()函数
// 真正地插入执行程序 _insert() // 返回新插入节点的迭代器 template<class Key , class Value , class KeyOfValue , class Compare , class Alloc> typename<Key , Value , KeyOfValue , Compare , Alloc>::_insert(base_ptr x_ , base_ptr y_ , const Value &v) { // 参数x_ 为新值插入点,参数y_为插入点之父节点,参数v为新值 link_type x = (link_type) x_; link_type y = (link_type) y_; link_type z; // key_compare 是键值大小比较准则。应该会是个function object if(y == header || x != 0 || key_compare(KeyOfValue()(v) , key(y) )) { z = create_node(v); // 产生一个新节点 left(y) = z; // 这使得当y即为header时,leftmost() = z if(y == header) { root() = z; rightmost() = z; } else if(y == leftmost()) // 如果y为最左节点 leftmost() = z; // 维护leftmost(),使它永远指向最左节点 } else { z = create_node(v); // 产生一个新节点 right(y) = z; // 令新节点成为插入点之父节点y的右子节点 if(y == rightmost()) rightmost() = z; // 维护rightmost(),使它永远指向最右节点 } parent(z) = y; // 设定新节点的父节点 left(z) = 0; // 设定新节点的左子节点 right(z) = 0; // 设定新节点的右子节点 // 新节点的颜色将在_rb_tree_rebalance()设定(并调整) _rb_tree_rebalance(z , header->parent); // 参数一为新增节点,参数二为根节点root ++node_count; // 节点数累加 return iterator(z); // 返回一个迭代器,指向新增节点 }
调整RB-tree
在将节点插入到RB-tree中后,需要调整RB-tree使之恢复平衡,调用_rb_tree_rebalance()
// 全局函数 // 重新令树形平衡(改变颜色及旋转树形) // 参数一为新增节点,参数二为根节点root inline void _rb_tree_rebalance(_rb_tree_node_base* x , _rb_tree_node_base*& root) { x->color = _rb_tree_red; //新节点必为红 while(x != root && x->parent->color == _rb_tree_red) // 父节点为红 { if(x->parent == x->parent->parent->left) // 父节点为祖父节点之左子节点 { _rb_tree_node_base* y = x->parent->parent->right; // 令y为伯父节点 if(y && y->color == _rb_tree_red) // 伯父节点存在,且为红 { x->parent->color = _rb_tree_black; // 更改父节点为黑色 y->color = _rb_tree_black; // 更改伯父节点为黑色 x->parent->parent->color = _rb_tree_red; // 更改祖父节点为红色 x = x->parent->parent; } else // 无伯父节点,或伯父节点为黑色 { if(x == x->parent->right) // 如果新节点为父节点之右子节点 { x = x->parent; _rb_tree_rotate_left(x , root); // 第一个参数为左旋点 } x->parent->color = _rb_tree_black; // 改变颜色 x->parent->parent->color = _rb_tree_red; _rb_tree_rotate_right(x->parent->parent , root); // 第一个参数为右旋点 } } else // 父节点为祖父节点之右子节点 { _rb_tree_node_base* y = x->parent->parent->left; // 令y为伯父节点 if(y && y->color == _rb_tree_red) // 有伯父节点,且为红 { x->parent->color = _rb_tree_black; // 更改父节点为黑色 y->color = _rb_tree_black; // 更改伯父节点为黑色 x->parent->parent->color = _rb_tree_red; // 更改祖父节点为红色 x = x->parent->parent; // 准备继续往上层检查 } else // 无伯父节点,或伯父节点为黑色 { if(x == x->parent->left) // 如果新节点为父节点之左子节点 { x = x->parent; _rb_tree_rotate_right(x , root); // 第一个参数为右旋点 } x->parent->color = _rb_tree_black; // 改变颜色 x->parent->parent->color = _rb_tree_red; _rb_tree_rotate_left(x->parent->parent , root); // 第一个参数为左旋点 } } }//while root->color = _rb_tree_black; // 根节点永远为黑色 } // 左旋函数 inline void _rb_tree_rotate_left(_rb_tree_node_base* x , _rb_tree_node_base*& root) { // x 为旋转点 _rb_tree_node_base* y = x->right; // 令y为旋转点的右子节点 x->right = y->left; if(y->left != 0) y->left->parent = x; // 别忘了回马枪设定父节点 y->parent = x->parent; // 令y完全顶替x的地位(必须将x对其父节点的关系完全接收过来) if(x == root) // x为根节点 root = y; else if(x == x->parent->left) // x为其父节点的左子节点 x->parent->left = y; else // x为其父节点的右子节点 x->parent->right = y; y->left = x; x->parent = y; } // 右旋函数 inline void _rb_tree_rotate_right(_rb_tree_node_base* x , _rb_tree_node_base*& root) { // x 为旋转点 _rb_tree_node_base* y = x->left; // 令y为旋转点的左子节点 x->left = y->right; if(y->right != 0) y->right->parent = x; // 别忘了回马枪设定父节点 y->parent = x->parent; // 令y完全顶替x的地位(必须将x对其父节点的关系完全接收过来) if(x == root) root = y; else if(x == x->parent->right) // x为其父节点的右子节点 x->parent->right = y; else // x为其父节点的左子节点 x->parent->left = y; y->right = x; x->parent = y; }
搜寻元素
// 寻找RBTree中是否存在键值为k的节点 template <class Key, class Value, class KeyOfValue, class Compare, class Alloc> typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::find(const Key& k) { link_type y = header; // Last node which is not less than k. link_type x = root(); // Current node. while (x != 0) // key_compare是节点键值大小比较函数 if (!key_compare(key(x), k)) // 如果节点x的键值大于k,则继续往左子树查找 y = x, x = left(x); // else // 如果节点x的键值小于k,则继续往右子树查找 x = right(x); iterator j = iterator(y); // y的键值不小于k,返回的时候需要判断与k是相等还是小于 return (j == end() || key_compare(k, key(j.node))) ? end() : j; }
set
所有元素都会根据元素的键值自动被排序,以RB-tree作为其底层机制,不允许通过set的迭代器来改变set的元素值,因为set的元素值就是键值,更改了元素值就会影响其排列规则,如果任意更改元素值,会严重破坏set组织,因此在定义set的迭代器时被定义成了RB-tree的const_iterator,它的键值就是实值。
它与list相同在操作前所有的迭代器在操作后仍然有效,被操作的那个迭代器除外。
template <class Key, class Compare = less<key>, class Alloc = allloc> class set { public: typedef key key_type; //键值与实值相同 typedef key value_type; typedef Compare key_compare; typedef Compare value_compare; private: //... typedef rb_tree<key_type, value_type, identify<value_type>, key_compare, Alloc> rep_type; rep_type t; //采用红黑树来表现set public: //... typedef typename rep_type::const_iterator iterator; //定义为const_iterator,不允许更改 //... //以下列举出的构造函数与插入均使用insert_unique方式 template <class InputIterator> set(InputIterator first, InputIterator lst) : t(Compare()) { t.insert_unique(first, last); } //... iterator insert(iterator position, const value_type& x) { //其中一个插入操作版本 typedef typename rep_type::iterator rep_iterator; return t.insert_unique((rep_iterator&)position, x); } //... void erase(iterator position) { //其中一个版本的删除操作 typedef typename rep_type::iterator rep_iterator; t.erase((rep_iterator&)position); } //... //在first和last的前闭后开的区间中进行二分查找第一个不小于x的值 iterator lower_bound(const key_type& x) const { return t.low_bound(x); } //在first和last的前闭后开的区间中进行二分查找第一个大于x的值 iterator upper_bound(const key_type& x) const { return t.upper_bound(x); } //返回上述两种方式返回的迭代器区间 pair<iterator, iterator> equal_range(const key_type& x) const { return t.equal_range(x); } //... };
multiset
与set特性完全相同,唯一差别在于它允许键值重复,因此插入操作采用的是底层机制RB-tree的insert_equal()而非insert_unique()
map
所有元素都会根据元素的键值自动被排序,map的所有元素都是pair,同时拥有实值和键值,pair的第一元素被视为键值,第二元素被视为元素值,map不允许两个元素拥有相同的键值,不能通过map的迭代器改变map的键值,因为map元素的键值关系到map元素的排列规则,任意改变map的元素键值会破坏map组织;但可以修正元素的实值。
重点分析subscript操作符:
T& operator[] (const key_type& k) { return (*((insert(value_type(k, T()))).first)).second; }//by reference传递,所以他为左值右值都可以
他能被当做左值引用和右值引用
map<string, int> simap; simap[string("jjhou")] = 1; //左值运用 int number = simap[string("jjhou")]; //右值引用
- 首先产生一个临时对象:value_type(k, T())
- 再将该元素插入到map中:insert(value_type(k, T()))
- 插入操作符返回一个pair,其第一个元素是迭代器指向插入妥当的新元素或插入失败(键值重复)的旧元素;下标操作符为左值引用(通常表示有新元素要添加),正好可以以“实值待填”将元素位置卡好;如果下标操作符为右值引用,通常表示键值取实值此时返回的pair的第一个元素恰指向键值符合的旧元素。(insert(value_type(k, T()))).first
- 第一元素是一个迭代器,提领该元素:*((insert(value_type(k, T()))).first)
- 获得一个map元素,由键值和实值组成,取第二元素:(*((insert(value_type(k, T()))).first)).second
hashtable
插入删除寻找具有常数事件,以统计为基础不需要输入元素具有随机性。
使用hash function(散列函数)将一元素映射为“大小之可接受索引”。为了避免不同元素映射到同一位置上也就是避免碰撞,可用以下几种方法。首先引入一个额外的概念负载系数——元素个数除以表格大小,除了开链以外,负载系数都是在0~1之间。
1.线性探测:计算出某个元素的插入位置时发现该位置已经不可用,就循序往下一次寻找可用的位置,达到尾端就绕到头部去寻找。在表格足够大并且每个元素都是独立的假设下,线性探测的最坏情况是巡访整个表格,平均情况是巡访一半的表格。但是他有一个缺点:除非新元素经过hash function直接落在#4-#7上,否则其永远不能被再用,因为#3是第一考虑的位置,因为不论新元素落在89012哪个位置最终都会落在#3上。不断解决碰撞问题,最后才得以插入成功,这就是主集团问题。
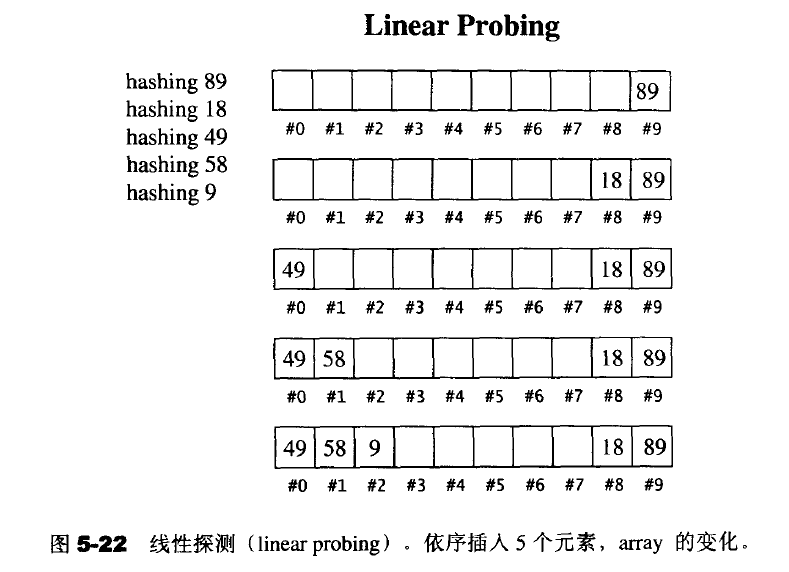
2.二次探测:如果hash function计算出的位置为H,而该位置被占用,那我们就尝试H+1^2,H+2^2......而不像线性探测那样H+1,H+2。。。它可消除主集团问题,但是却又带来次集团问题:两个元素经hash function计算出位置相同,则插入时所探测的位置也相同。
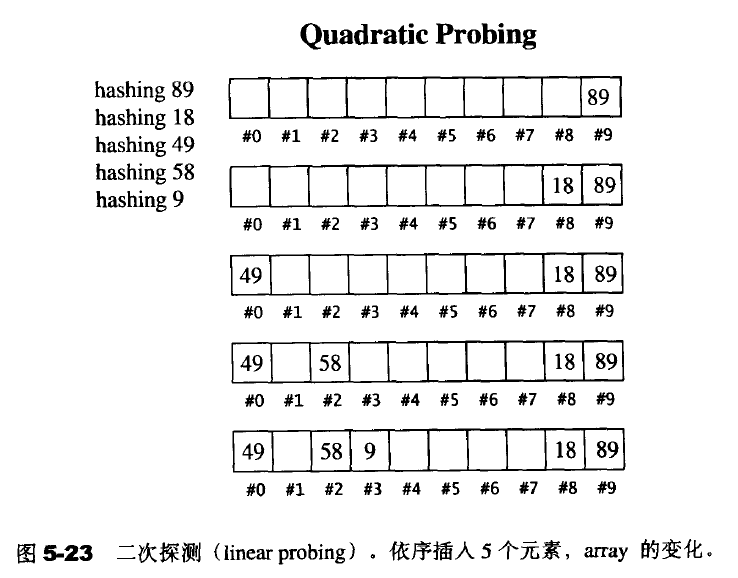
3.开链:在每个表格的元素中维护一个list,hash function为我们分配某一个list,我们在list上执行插入删除寻找操作,针对list的操作是一种线性操作。SGI STL以质数来设计表格大小,并将28个质数计算好放置(以53为起始,大约二倍增长,*2-1)
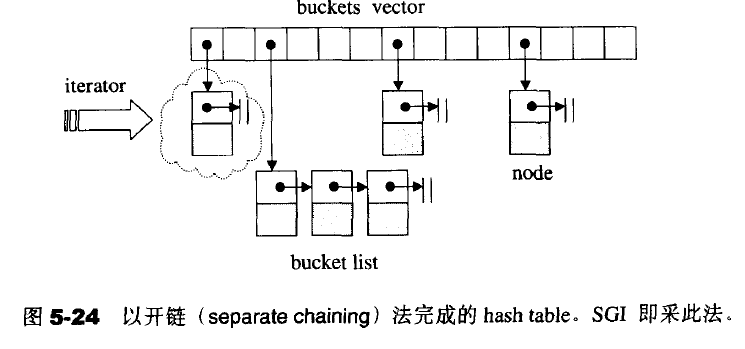
hashtable的迭代器
他必须维护与整个“buckets vector”的关系,并记录目前所指的结点,前进操作首先是目前所指结点出发,前进一个位置,由于该结点被安置于list内,所以用next可以完成前进操作,如果是list的尾端结点,就跳至下一个bucket上,指向其开头元素。他只有operator++&operator++(int),没有operator--,也就是无后退操作。
hashtable的数据结构
/* Value:节点值类型 Key:节点的键值类型 HashFcn:仿函数,计算hash值 ExtractKey:仿函数,提取key值 EqualKey:仿函数,判别键值是否相同的方法 Alloc:空间配置器 */ template <class Value, class Key, class HashFcn, class ExtractKey, class EqualKey, class Alloc> class hashtable { public: typedef HashFcn hasher; typedef EqualKey key_equal; typedef size_t size_type; private: hasher hash; key_equal equals; ExtractKey get_key; typedef __hashtable_node<Value> node; typedef simple_alloc<node, Alloc> node_allocator; vector<node*, Alloc> buckets; size_type num_elements; public: size_type bucket_count() const { return buckets.size(); } }
插入操作
// 插入数据不允许重复 pair<iterator, bool>insert_unique(const value_type& obj) { resize(num_elements + 1); // 判断表格vector是否需要重建,如果需要就重建 return insert_unique_noresize(obj); // 插入键值,不允许重复 } void resize(size_type num_elements_hint)//如果不需要重建表格立刻返回 { const size_type old_n = buckets.size(); if(num_elements_hint > old_n) { const size_type n=next_size(num_elements_hint);//找出下一质数,也就是最接近某数并大于某数的质数 if(n>old_n) { vector<node*, Alloc> tmp(n, (node*)0); for(size_type bucket = 0; bucket < old_n; ++bucket) { node* first = buckets[bucket]; while(first) { size_type new_bucket = bkt_num(first->val, n);//找出结点应该落在哪一个新的bucket内 buckets[bucket] = first->next;//令旧的bucket指向所对应的串的下一结点 first->next = tmp[new_bucket];//将当前节点插入新bucket内,成为其对应串的第一个结点 tmp[new_bucket] = first;// first = buckets[bucket];//回到旧的bucket所指待处理串,准备处理下一结点 } } buckets.swap(tmp); } } } pair<iterator, bool> insert_unique_noresize(const value_type& obj) { const size_type n = bke_num(obj); node* first = buckets[n]; for(node* cur = first; cur; cur = cur->next) { if(equals(get_key(cur->val), get_key(obj))) { return pair<iterator, bool>(iterator(cur, this), false); } } node* tmp = new_node(obj); tmp->next = first; bucklet[n] = tmp; ++num_elements; return pair<iterator, bool>(iterator(tmp, this), true); } // 插入数据允许重复 iterator insert_equal(const value_type& obj) { resize(num_elements + 1); // 判断表格vector是否需要重建,如果需要就重建 return insert_equal_noresize(obj); // 插入键值,允许重复 } iterator insert_equal_noresize(const value_type& obj) { const size_type n = bke_num(obj); node* first = buckets[n]; for(node* cur = first; cur; cur = cur->next) { if(equals(get_key(cur->val), get_key(obj))) { // 如果有key相同的节点,将新节点插入在相同节点的后面 node* tmp = new_node(obj); tmp->next = cur->next; cur->next = tmp; ++num_elements; return iterator(tmp, this); } } node* tmp = new_node(obj); tmp->next = first; bucklet[n] = tmp; ++num_elements; return iterator(tmp, this); } // 映射函数 size_type bkt_num(const value_type& obj, size_t n) const { return bkt_num_key(get_key(obj), n); } size_type bkt_num(const value_type& obj) const { return bkt_num_key(get_key(obj)); } size_type bkt_num_key(const key_type& key) const { return bkt_num_key(get_key(obj), buckets.size()); } // 最底层干活的函数 size_type bkt_num_key(const key_type& key, size_t n) const { // STL为所有的基础类型都定义了hash函数 return hash(key) % n; }
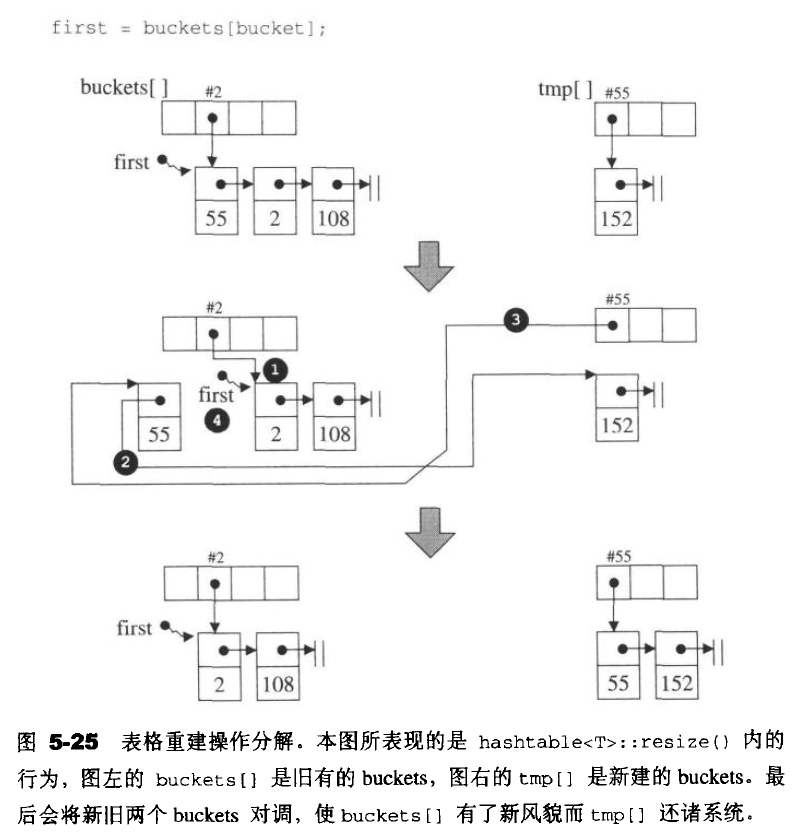
在调用clear清除时,只是把bucket内容为nullptr,并未释放bucket vector的空间。
hash function
stl内建哈希函数,针对char、short、long、int这些类型只是简单的返回其数值,但是对于char*会调用以下版本hash(stl内建的只有只几种类型和其unsigned版本)
inline size_t __stl_hash_string(const char* s) { unsigned long h = 0; for( ;*s;++s) h = 5*h + *s; return size_t(h); }
hash_set
hash_set无自动排序功能。其余与set相同。
template <class Value, class HashFcn = hash<Value>, class EqualKey = equal_to<Value>, class Alloc = alloc> class hash_set { private: // 底层为hashtable typedef hashtable<Value, Value, HashFcn, identity<Value>, EqualKey, Alloc> ht; ht rep; public: typedef typename ht::key_type key_type; typedef typename ht::value_type value_type; typedef typename ht::hasher hasher; typedef typename ht::key_equal key_equal; typedef typename ht::size_type size_type; typedef typename ht::difference_type difference_type; typedef typename ht::const_pointer pointer; typedef typename ht::const_pointer const_pointer; typedef typename ht::const_reference reference; typedef typename ht::const_reference const_reference; typedef typename ht::const_iterator iterator; typedef typename ht::const_iterator const_iterator; hasher hash_funct() const { return rep.hash_funct(); } key_equal key_eq() const { return rep.key_eq(); } public: // 默认构造100大小的hashtable,将会被调整为大于100的预定义质数 hash_set() : rep(100, hasher(), key_equal()) {} explicit hash_set(size_type n) : rep(n, hasher(), key_equal()) {} hash_set(size_type n, const hasher& hf) : rep(n, hf, key_equal()) {} hash_set(size_type n, const hasher& hf, const key_equal& eql) : rep(n, hf, eql) {} // 所有的插入操作都是insert_unique,不允许键值重复 template <class InputIterator> hash_set(InputIterator f, InputIterator l) : rep(100, hasher(), key_equal()) { rep.insert_unique(f, l); } template <class InputIterator> hash_set(InputIterator f, InputIterator l, size_type n) : rep(n, hasher(), key_equal()) { rep.insert_unique(f, l); } template <class InputIterator> hash_set(InputIterator f, InputIterator l, size_type n, const hasher& hf) : rep(n, hf, key_equal()) { rep.insert_unique(f, l); } template <class InputIterator> hash_set(InputIterator f, InputIterator l, size_type n, const hasher& hf, const key_equal& eql) : rep(n, hf, eql) { rep.insert_unique(f, l); } public: // 所有操作几乎都是直接调用hashtable的接口 size_type size() const { return rep.size(); } size_type max_size() const { return rep.max_size(); } bool empty() const { return rep.empty(); } void swap(hash_set& hs) { rep.swap(hs.rep); } friend bool operator== __STL_NULL_TMPL_ARGS(const hash_set&, const hash_set&); iterator begin() const { return rep.begin(); } iterator end() const { return rep.end(); } public: pair<iterator, bool> insert(const value_type& obj) { pair<typename ht::iterator, bool> p = rep.insert_unique(obj); return pair<iterator, bool>(p.first, p.second); } #ifdef __STL_MEMBER_TEMPLATES template <class InputIterator> void insert(InputIterator f, InputIterator l) { rep.insert_unique(f, l); } #else void insert(const value_type* f, const value_type* l) { rep.insert_unique(f, l); } void insert(const_iterator f, const_iterator l) { rep.insert_unique(f, l); } #endif /*__STL_MEMBER_TEMPLATES */ pair<iterator, bool> insert_noresize(const value_type& obj) { pair<typename ht::iterator, bool> p = rep.insert_unique_noresize(obj); return pair<iterator, bool>(p.first, p.second); } iterator find(const key_type& key) const { return rep.find(key); } size_type count(const key_type& key) const { return rep.count(key); } pair<iterator, iterator> equal_range(const key_type& key) const { return rep.equal_range(key); } size_type erase(const key_type& key) { return rep.erase(key); } void erase(iterator it) { rep.erase(it); } void erase(iterator f, iterator l) { rep.erase(f, l); } void clear() { rep.clear(); } public: void resize(size_type hint) { rep.resize(hint); } size_type bucket_count() const { return rep.bucket_count(); } size_type max_bucket_count() const { return rep.max_bucket_count(); } size_type elems_in_bucket(size_type n) const { return rep.elems_in_bucket(n); } };
hash_map
template <class Key, class T, class HashFcn = hash<Key>, class EqualKey = equal_to<Key>, class Alloc = alloc> class hash_map { private: // 底层为hashtable typedef hashtable<pair<const Key, T>, Key, HashFcn, select1st<pair<const Key, T> >, EqualKey, Alloc> ht; ht rep; public: typedef typename ht::key_type key_type; typedef T data_type; typedef T mapped_type; typedef typename ht::value_type value_type; typedef typename ht::hasher hasher; typedef typename ht::key_equal key_equal; typedef typename ht::size_type size_type; typedef typename ht::difference_type difference_type; typedef typename ht::pointer pointer; typedef typename ht::const_pointer const_pointer; typedef typename ht::reference reference; typedef typename ht::const_reference const_reference; typedef typename ht::iterator iterator; typedef typename ht::const_iterator const_iterator; hasher hash_funct() const { return rep.hash_funct(); } key_equal key_eq() const { return rep.key_eq(); } public: // 默认构造100大小的hashtable,将会被调整为大于100的预定义质数 hash_map() : rep(100, hasher(), key_equal()) {} explicit hash_map(size_type n) : rep(n, hasher(), key_equal()) {} hash_map(size_type n, const hasher& hf) : rep(n, hf, key_equal()) {} hash_map(size_type n, const hasher& hf, const key_equal& eql) : rep(n, hf, eql) {} // 所有的插入操作都是insert_unique,不允许键值重复 template <class InputIterator> hash_map(InputIterator f, InputIterator l) : rep(100, hasher(), key_equal()) { rep.insert_unique(f, l); } template <class InputIterator> hash_map(InputIterator f, InputIterator l, size_type n) : rep(n, hasher(), key_equal()) { rep.insert_unique(f, l); } template <class InputIterator> hash_map(InputIterator f, InputIterator l, size_type n, const hasher& hf) : rep(n, hf, key_equal()) { rep.insert_unique(f, l); } template <class InputIterator> hash_map(InputIterator f, InputIterator l, size_type n, const hasher& hf, const key_equal& eql) : rep(n, hf, eql) { rep.insert_unique(f, l); } public: size_type size() const { return rep.size(); } size_type max_size() const { return rep.max_size(); } bool empty() const { return rep.empty(); } void swap(hash_map& hs) { rep.swap(hs.rep); } friend bool operator== __STL_NULL_TMPL_ARGS(const hash_map&, const hash_map&); iterator begin() { return rep.begin(); } iterator end() { return rep.end(); } const_iterator begin() const { return rep.begin(); } const_iterator end() const { return rep.end(); } public: pair<iterator, bool> insert(const value_type& obj) { return rep.insert_unique(obj); } #ifdef __STL_MEMBER_TEMPLATES template <class InputIterator> void insert(InputIterator f, InputIterator l) { rep.insert_unique(f, l); } #else void insert(const value_type* f, const value_type* l) { rep.insert_unique(f, l); } void insert(const_iterator f, const_iterator l) { rep.insert_unique(f, l); } #endif /*__STL_MEMBER_TEMPLATES */ pair<iterator, bool> insert_noresize(const value_type& obj) { return rep.insert_unique_noresize(obj); } iterator find(const key_type& key) { return rep.find(key); } const_iterator find(const key_type& key) const { return rep.find(key); } T& operator[](const key_type& key) { return rep.find_or_insert(value_type(key, T())).second; } size_type count(const key_type& key) const { return rep.count(key); } pair<iterator, iterator> equal_range(const key_type& key) { return rep.equal_range(key); } pair<const_iterator, const_iterator> equal_range(const key_type& key) const { return rep.equal_range(key); } size_type erase(const key_type& key) { return rep.erase(key); } void erase(iterator it) { rep.erase(it); } void erase(iterator f, iterator l) { rep.erase(f, l); } void clear() { rep.clear(); } public: void resize(size_type hint) { rep.resize(hint); } size_type bucket_count() const { return rep.bucket_count(); } size_type max_bucket_count() const { return rep.max_bucket_count(); } size_type elems_in_bucket(size_type n) const { return rep.elems_in_bucket(n); } };



