manacher
manacher:是一个可以在O(n)的复杂度中返回字符串s中最长回文子串长度的算法。
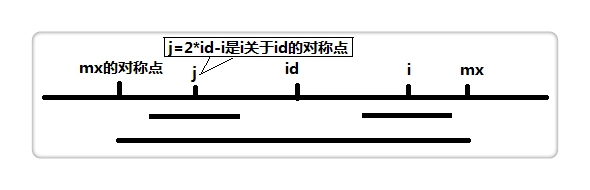
关于:
arr[i]=maxR>i?min(arr[2*id-i],maxR-i):1;
其中arr[i]是以i为中心的最长回文半径,maxR是最右侧回文半径相当于上图中mx,min的作用是(用上图来解释):计算arr数组的值是从左向右计算的,在计算i的回文半径时,j的回文半径已经计算过,所以arr[2*id-i]其实就是arr[j],但是arr[j]与mx-i的大小关系未知,并且mx是我们已知的最右回文半径,mx左侧的情况未知,所以当arr[j]的值超过mx-i时,我们只能取到mx-i,以i为中心且mx右侧的情况只能一点一点向外扩。
class Solution { public: string longestPalindrome(string s) { if(s.size()<0) return ""; //解决奇偶回文 string str("#"); for(auto it=s.begin();it!=s.end();++it) { str+=(*it); str+="#"; } //以i为中心的最右回文半径 vector<int> arr(str.length(),0); int maxR=0,id=0;//最右回文半径(不包括此值)和回文中心 int resId=0,resLen=0;//存储结果回文中心和回文半径 for(int i=0;i<str.length();++i) { //在maxR内,i与id对应的j,对应的回文半径相等 //i与maxR的关系: // 1>i在maxR内,直接根据j求得 // 2>j>=maxR,要依次判断尝试 arr[i]=maxR>i?min(arr[2*id-i],maxR-i):1;//i在回文半径内,直接可根据回文特性计算得出 while(i+arr[i]<str.length()&&i-arr[i]>=0)//i不在回文半径内需要依次向两边扩&&在回文半径内也需要判断回文半径外是否存在回文 if(str[i+arr[i]]==str[i-arr[i]]) ++arr[i]; else break; if(maxR<i+arr[i])//更新回文半径和回文中心 { id=i; maxR=i+arr[i]; } if(resLen<arr[i]) { resId=i; resLen=arr[i]; } } return s.substr((resId-resLen+1)/2,resLen-1); } };



