最小生成树——kruskal算法
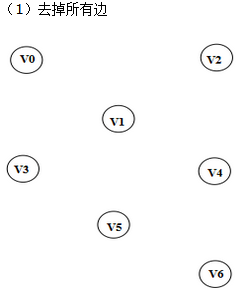
- 将n个顶点看成n个集合
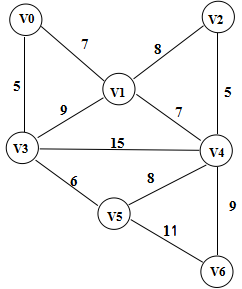
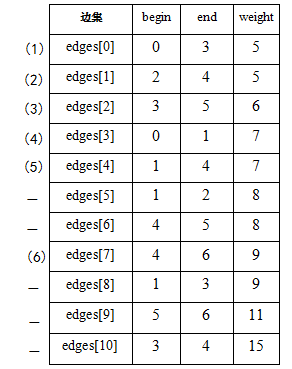
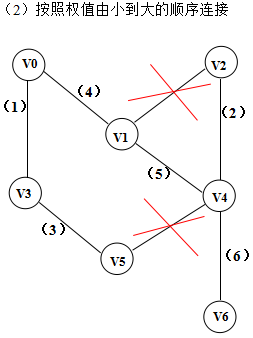
- 按权值由小到大的顺序选择边,所选边应满足两个顶点不在同一个顶点集合内,将该边放到生成树的结合边中,同时也将该边的两个定点放到生成树的顶点集中
- 重复前两个(注意:所加的边不能构成环,所以在以下代码中用find函数检测将该边加入是否存在环)
适合于稀疏图——顶点多边少
#include <iostream> #include <vector> #include <algorithm> using namespace std; const int INF=0x3f3f; //边集数组 typedef struct Edg { int begin;//该边的起始点 int end;//该边的结束点 int weight;//该边的权值 Edg() { begin=end=weight=0; } }Edg; class Cmp { public: bool operator() (const Edg &a,const Edg &b) { return a.weight<=b.weight; } }; class Graph { private: int num; int e; vector<vector<int> > arr; vector<Edg> edg; vector<int> tree; int find(vector<int> &t,int n);//判断该边的两个定点是否都在最小生成树的集合中,v[t]=k,t是边的起始点,k是边的结束点 public: Graph(); ~Graph(); void kruskal(); }; Graph::Graph() { cout<<" num"<<endl; cin>>num; cout<<" e"<<endl; cin>>e; arr.resize(num); for(int i=0;i<num;++i) { arr.at(i).resize(num); fill(arr.at(i).begin(),arr.at(i).end(),INF); } edg.resize(num);// tree.resize(num,-1);//最小生成树的顶点集合,该集合中最多和图中的点一样多 cout<<" 输入边的两个端点&&权值"<<endl; pair<int,int> info; for(int i=0;i<e;++i) { cin>>info.first>>info.second; cin>>arr.at(info.first-1).at(info.second-1); arr.at(info.second-1).at(info.first-1)=arr.at(info.first-1).at(info.second-1); } } Graph::~Graph() { //cout<<"~Graph()"<<endl; } int Graph::find(vector<int> &t,int n) { while(t.at(n)>0) n=t.at(n); return n; } void Graph::kruskal() { //储存边的信息,只存储邻接矩阵的对角线右上部分,无向图 for(int i=0;i<num;++i) for(int j=i+1;j<num;++j) { if(arr.at(i).at(j)<INF) { edg.at(i).begin=i; edg.at(i).end=j; edg.at(i).weight=arr.at(i).at(j); } } //按权值从小到大把边集排序 sort(edg.begin(),edg.end(),Cmp()); for(int i=0;i<num;++i) { int t=find(tree,edg.at(i).begin); int t1=find(tree,edg.at(i).end); if(t1!=t) { tree.at(t)=t1; cout<<"<"<<edg.at(i).begin<<","<<edg.at(i).end<<"> weight:"<<edg.at(i).weight<<endl; } } } int main() { Graph g; g.kruskal(); return 0; }



