礼物的最大价值

题目

　　在一个m*n的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向左或者向下移动一格，知道到达棋盘的右下角。给定一个棋盘及其上面的礼物，请计算你最多能拿多少价值的礼物？

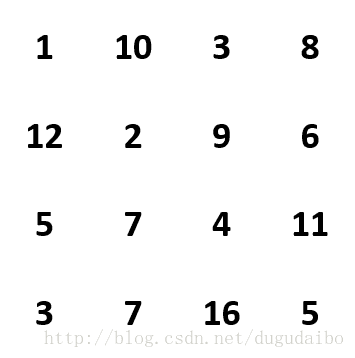
思路

一、利用循环的动态规划

1. 定义f(i,j)表示到达坐标为(i,j)的格子时能拿到的礼物总和的最大值；
2. 有两种路径到达(i,j)：（i-1,j）或者（i,j-1）；
3. f(i,j) = max(f(i-1,j), f(i,j-1)) + gift[i,j]；
4. 使用循环来计算避免重复子问题。

二、优化空间复杂度，使用一维数组

　　每次计算拿到的礼物最大值的时候，最大值的坐标只依赖(i-1,j)and(i,j-1)两个格子，因此第i-2行及以上所有的格子礼物最大值没有必要保存下来，因此可以用一维数组代替二维数组，一维数组的长度为棋盘的列数，当我们计算坐标为(i,j)格子能够拿到礼物的最大价值f(i,j)的时候，数组钱j个数字分别是f(i,0),f(i,1)...,f(i,j-1)，数组从下标为j的数字开始到最后一个数字，分别为f(i-1,j),f(i-1,j+1),...,f(i-1,n-1)，也就是数组前面j个数字分别是当前第i行前面j个格子礼物的最大值，而后的数字分别保存前面第i-1行n-j个格子礼物的最大值。

1.

 

class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        if (grid.empty() || grid[0].empty()) {
            return 0;
        }

        vector<vector<int>> max_value(grid.size(), vector<int>(grid[0].size(), 0));
        for (int i = 0; i < grid.size(); ++i) {
            for (int j = 0; j < grid[0].size(); ++j) {
                if (i == 0 && j ==0 ) {
                    max_value[i][j] = grid[i][j];
                }
                else if (i == 0) {
                    max_value[i][j] = max_value[i][j - 1] + grid[i][j];
                }
                else if (j == 0) {
                    max_value[i][j] = max_value[i - 1][j] + grid[i][j];
                }
                else {
                    max_value[i][j] = max(max_value[i - 1][j], max_value[i][j - 1]) + grid[i][j];
                }                
            }
        }
        return max_value[grid.size() - 1][grid[0].size() - 1];
    }
};

2.

#include <iostream>
#include <vector>
#include <fstream>
using namespace std;

class Solution
{
    public:
        int get_max_value(const vector<vector<int> > &v);
};
int Solution::get_max_value(const vector<vector<int> > &v)
{
    if(v.empty()||v.size()<=0||v[0].size()<=0)
        return -1;
    
    //保存每一步拿到的礼物的最大值
    //每次计算拿到的礼物最大值的时候，最大值的坐标只依赖(i-1,j)and(i,j-1)两个格子，因此第
    //i-2行及以上所有的格子礼物最大值没有必要保存下来，因此可以用一维数组代替二维数组，
    //一维数组的长度为棋盘的列数，当我们计算坐标为(i,j)格子能够拿到礼物的最大价值f(i,j)的
    //时候，数组钱j个数字分别是f(i,0),f(i,1)...,f(i,j-1)，数组从下标为j的数字开始到最后一个
    //数字，分别为f(i-1,j),f(i-1,j+1),...,f(i-1,n-1)，也就是数组前面j个数字分别是当前第i行
    //前面j个格子礼物的最大值，而后的数字分别保存前面第i-1行n-j个格子礼物的最大值 
    vector<int> value(v[0].size(),0);
    for(int i=0;i<v.size();++i)
    {
        for(int j=0;j<v[0].size();++j)
        {
            int left=0;
            int up=0;
            
            if(i>0)
                up=value[j];
            if(j>0)
                left=value[j-1];
                
            value[j]=max(up,left)+v[i][j];
        }
    }
    return value[v[0].size()-1];
}

int main()
{
    ifstream in("1.txt");
    vector<vector<int> > v(4,vector<int>(4,0));
    for(int i=0;i<4;++i)
        for(int j=0;j<4;++j)
            in>>v[i][j];
    
    Solution s;
    cout<<s.get_max_value(v)<<endl;
    return 0;
}

 3.

class Solution {
private:
    int maxValueCore(const vector<vector<int>>& grid, int i, int j) {
        if (i < 0 || j < 0) {
            return 0;
        }

        return max(maxValueCore(grid, i - 1, j), maxValueCore(grid, i, j - 1)) + grid[i][j];
    }
public:
    int maxValue(vector<vector<int>>& grid) {
        if (grid.empty() || grid[0].empty()) {
            return 0;
        }

        return maxValueCore(grid, grid.size() - 1, grid[0].size() - 1);
    }
};