复键day1 Codeforces.545C Woodcutters

这个也算是经典老问题了，横轴给了n棵树，每个树高度不同，砍树，可以选择，砍掉往左右任意一个方向倒，或者留着不砍。

前提要求是树如果要砍掉的话，倒下来不能压到树根或者前面放倒的树，问最多能砍掉几棵树。

我本来一上来没思路，想看答案，后来捋了捋，发现还是可做的，要是1500没做出来说明自己也太废了

然后发现这个问题很dp

主要思路如下

 

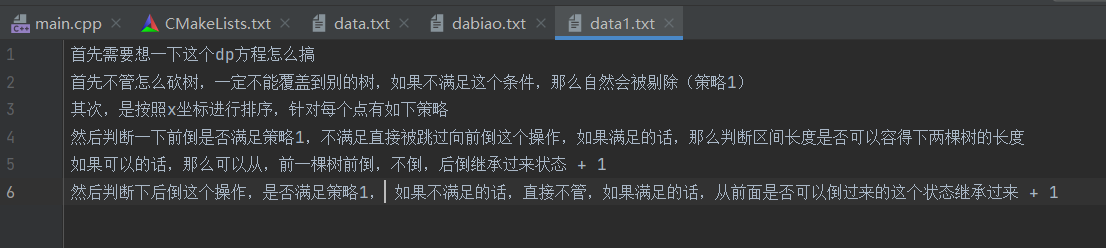
 然后按照这个写了写发现答案不对，后来发现自己是没处理压树根的情况，两棵树之间的距离要大于高度h才能放倒，那没事了

#include <bits/stdc++.h>

using namespace std;
#define limit (1000000 + 5)//防止溢出
#define INF 0x3f3f3f3f
#define inf 0x3f3f3f3f3f
#define lowbit(i) i&(-i)//一步两步
#define EPS 1e-9
#define FASTIO  ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);
#define ff(a) printf("%d\n",a );
#define pi(a, b) pair<a,b>
#define rep(i, a, b) for(ll i = a; i <= b ; ++i)
#define per(i, a, b) for(ll i = b ; i >= a  ; --i)
#define MOD 998244353
#define traverse(u) for(int i = head[u]; ~i ; i = edge[i].next)
#define FOPEN freopen("C:\\Users\\tiany\\CLionProjects\\akioi\\data.txt", "rt", stdin)
#define FOUT freopen("C:\\Users\\tiany\\CLionProjects\\akioi\\dabiao.txt", "wt", stdout)
typedef long long ll;
typedef unsigned long long ull;
char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;

inline ll read() {
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
    ll sign = 1, x = 0;
    char s = getchar();
    while (s > '9' || s < '0') {
        if (s == '-')sign = -1;
        s = getchar();
    }
    while (s >= '0' && s <= '9') {
        x = (x << 3) + (x << 1) + s - '0';
        s = getchar();
    }
    return x * sign;
#undef getchar
}//快读
void print(ll x) {
    if (x / 10) print(x / 10);
    *O++ = x % 10 + '0';
}

void write(ll x, char c = 't') {
    if (x < 0)putchar('-'), x = -x;
    print(x);
    if (!isalpha(c))*O++ = c;
    fwrite(obuf, O - obuf, 1, stdout);
    O = obuf;
}


const ll mod = 1e9 + 7;

ll quickPow(ll base, ll expo) {
    ll ans = 1;
    while (expo) {
        if (expo & 1)(ans *= base) %= mod;
        expo >>= 1;
        base = base * base;
        base %= mod;
    }
    return ans % mod;
}

ll C(ll n, ll m) {
    if (n < m)return 0;
    ll x = 1, y = 1;
    if (m > n - m)m = n - m;
    rep(i, 0, m - 1) {
        x = x * (n - i) % mod;
        y = y * (i + 1) % mod;
    }
    return x * quickPow(y, mod - 2) % mod;
}

ll lucas(ll n, ll m) {
    return !m || n == m ? 1 : C(n % mod, m % mod) * lucas(n / mod, m / mod) % mod;
}


int n, m, k;
int a[limit];
int b[limit];
int dp[limit][3];//0 不动， 1向前，2向后
struct node{
    int x, r;
    bool operator<(const node &rhs)const{
        return x < rhs.x;
    }
}p[limit];
void solve() {
    cin>>n;
    rep(i, 1,n){
        cin>>a[i]>>b[i];
        p[i].x = a[i], p[i].r = b[i];
    }
    if(n == 1){
        cout<<1<<endl;
        return;
    }
    fill(dp[0], dp[0] + 3, 0);
    int ans = 0;
    rep(i,1,n){
        const auto &cur = p[i];
        if(i == 1){
            dp[i][1] = 1;
            dp[i][2] = (p[i + 1].x - p[i].x > p[i].r);
            continue;
        }
        //判断前倒是否可行,往前倒是否可以
        if(cur.x - p[i - 1].x > cur.r){
            dp[i][1] = max(dp[i - 1][0], dp[i - 1][1]) + 1;
            if(cur.x - p[i - 1].x > cur.r + p[i - 1].r){
                dp[i][1] = max(dp[i][1], dp[i - 1][2] + 1);
            }
        }
        //继承这个状态
        dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);
        dp[i][0] = max(dp[i][0], dp[i - 1][2]);
        if(i == n){
            dp[i][2] = max({dp[i - 1][1], dp[i - 1][0], dp[i - 1][2]}) + 1;
        }else{
            if(p[i + 1].x - cur.x > cur.r){
                dp[i][2] = max({dp[i - 1][0], dp[i - 1][1], dp[i - 1][2]}) + 1;
            }else{
                dp[i][2] = 0;
            }
        }

    }
    rep(i,1,n){
        rep(j,0,2){
            ans = max(ans, dp[i][j]);
//            cout<<i<<","<<j<<": "<<dp[i][j]<<endl;
        }
    }
    cout<<ans<<endl;
}

int32_t main() {
#ifdef LOCAL
    FOPEN;
//    FOUT;
#endif
    FASTIO
//    int kase;
//    cin >> kase;
//    while (kase--)
        solve();
    cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";
    return 0;
}