【算法复习四】计算复杂性与算法分析---组合数学知识汇总

一，组合数学问题

        1）排列定义  

            • 从n个不同的元素中，取r个不重复的元素，按次序排列，称为从n个中取r个的无重排列。

            •排列的全体组成的集合用P(n,r)表示。当r=n时称为全排列。

 

            组合定义  

             • 定义从n个不同元素中取r个不重复的元素组成一个子集，而不考虑其元素的顺序，称为从n个中取r个的无重组合。

             • 组合的全体组成的集合用C(n,r)表示。

        

       2）例题一：某车站有6个入口处，每个入口处每次只能进一人，一组9个人进站的方案有多少？

 

          【解法】一进站方案表示成：

                       00011001010100

           其中“0”表示人，“1”表示门框，其中“0”是不同元，“1”是相同元。给“1”n个门只用n-1个门框。任意进站方案可表示成上面14个元素的一个排列。

           [解法1]

                    分析：第一个人可以有6种进站的方式，也就是从6个入口的任意一个站进站，那么第二个人也可以有6种选择入口的方法，但是假如他和第一个人选择的入口是相同的话，就有谁在前的情况，所以第二个人就有了7种进站方案；同理，第三个人进站的话就有8种进站方案，这样算下去，那么第九个人就有14种进站的方法。

             

                  故所求方案为   14!/5!=6×7×8×...×14=726485720  

         [解法2]

                   在14个元的排列中先确定“1”的位置，有C(14,5)种选择，在确定人的位置，有9！种选择。

　　　        故　C(14,5)*9!　即所求：14!/5! 

                   注意：C(14,5)= （14! - （14-5）！）/ 5！

                   如：a10 a3 a40 a6 a70 a9 a100 a120 a14

                   方案为（2,5,8,11,13）

        

         例题二：简单格路径数问题 （类腾讯笔试题）

               从 (0,0)点出发沿x轴或y轴的正方向每步走一个单位，最终走到(m,n)点，有多少条路径？

              【分析】• 无论怎样走法，在x方向上总共走m步，在y方向上总共走n步。若用一个x表示x方向上的一步，一个字母y表示y方向上的一步。

                            • 则(0,0)→(m,n)的每一条路径可表示为m个x与n个y的一个有重排列。将每一个有重排列的x与y分别编号，可得m!*n!个m+n元的无重全排列。

              【分析】向上可以走m步，向右可以走n步。注意，必须向上走m步，向右走n步才能到达（m，n）

                          只需要考虑上和右依次在哪里出现，所以不难得出答案  C（m+n，n）=C（m+n，m）

 

        3）容斥原理

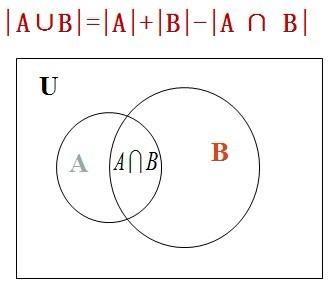
             •最简单的计数问题是求有限集合A和B的并的元素数目。显然有

             • 定理：即具有性质A或B的元素的个数等于具有性质A和B的元素个数。

         求a,b,c,d,e,f六个字母的全排列中不允许出现ace和df图象的排列数。

        解：设A为ace作为一个元素出现的排列集，B为df作为一个元素出现的排列集， A∩B为同时出现ace、df的排列数。

                • |A|=4！|B|=5！ |A∩B|=3！

                  |A∩B|= 6!- (5!+4!)+3!=582

       4） 容斥与鸽巢原理

              鸽巢原理之一： 鸽巢原理是组合数学中最简单也是最基本的原理，也叫抽屉原理。即“若有n个鸽子巢，n+1个鸽子，则至少有一个巢内有至少有两个鸽子。”

                   • 367人中至少有２人的生日相同。

                   • 10双手套中任取11只，其中至少有两只是完整配对的。

                   • 参加一会议的人中至少有２人认识的别的参加者的人数相等。

 

             鸽巢原理之二：m1 , m2 , … , mn都是正整数，并有m1 + m2 +… +mn－n + 1个鸽子住进n个鸽巢，则至少对某个 i有第 i个巢中至少有mi个鸽子，i = 1 , 2 , … , n．

                   •显然，鸽巢原理之一是鸽巢原理之二的特殊情况，即m1 = m2 = … = mn= 2，如若不然，则对任意 i， 都有第i个巢中的鸽子数≤mi－1　则，鸽子总数≤ m1 + m2 +… +mn－n，与假设相矛盾．

             

              例题一：拉蒙赛（Ramsey）问题

                            6 个人中至少存在３人相互认识或者相互不认识

                           •证：这个问题与凸六边形完全图的内边着二色，存在同色三角形等价．假定用红蓝着色．

                           • 设凸六边形完全图的顶点集为{v1, v2 , ··· , v6 }，dr(v)表示与顶点v 关联的红色边的条数，db(v)表示与v 关联的蓝色边的条数．在凸六边形完全图中，有dr(v)＋db(v)＝５，由鸽巢原理可知，至少有３条边同色．

    

             例题二：拉丁方

                        • 有1,2,3..,n构成的n╳n方阵，（aij）n╳n

                        要求：每行每列1,2,3..,n各出现一次。称为拉丁方。

 

二，生成函数

          生成函数定义

              • 对于序列a0,a1,a2,a3,a4……构造一函数：G(x) = a0 + a1x + a2x`2 + ……称函数G(x)是序列a0,a1,a2,a3,a4……的生成函数。

              •例如：（1+x）`n是C(n,0)，C(n,1)，C(n,2)……C(n,n)的生成函数。

              •如若已知序列a0,a1,a2,a3,a4……则对应的生成函数G(x)便可根据定义给出。反之亦然。

            例题：由红球两个，白球、黄球各一个，试求有多少种不同的组合方案

           一个球：3

           二个球：4

           三个球：3

           四个球：1      总共：12种

 

三，指数型生成函数

 

         指数型生成函数的概念

             • 设有n个元素，其中元素a1重复了n1 次，元素a2重复了n2 次，…，ak重复了nk次，从中取r个排列，求不同的排列数.

             • 如果n1 = n2 = n3 = …… nk = 1，则是一般的排列问题。

          现在由于出现重复，故不同的排列计数便比较复杂。先考虑n个元素的全排列，若n个元素没有完全一样的元素，则应有n!  种排列。若考虑ni 个元素ai 的全排列数为ni!，则真正不同的排列数为  n! /(n1!*n2!*……nk!)