图和图算法

1 词汇和定义

　　顶点（也称为“节点”）是图的基本部分。它可以有一个名称，我们将称为“键”。一个顶点也可能有额外的信息。我们将这个附加信息称为“有效载荷”。

　　边（也称为“弧”）是图的另一个基本部分。边连接两个顶点，以表明它们之间存在关系。边可以是单向的或双向的。如果图中的边都是单向的，我们称该图是有向图 。

　　权重 边可以被加权以示出从一个顶点到另一个顶点的成本。例如，在将一个城市连接到另一个城市的道路的图表中，边上的权重可以表示两个城市之间的距离。

　　利用这些定义，我们可以正式定义图。图可以由 G 表示，其中 G =(V，E) 。对于图 G，V 是一组顶点，E 是一组边。每个边是一个元组 (v，w) ，其中 w,v ∈ V 。我们可以添加第三个组件到边元组来表示权重。子图 s 是边 e 和顶点 v 的集合，使得 e⊂E 和 v⊂V 。

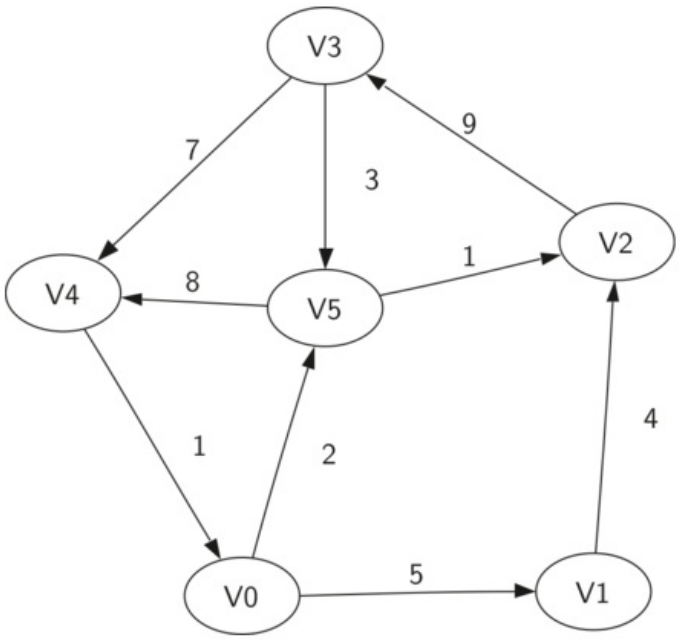
　　上图展示了简单加权有向图的另一示例。正式地，我们可以将该图表示为六个顶点的集合：V={V0,V1,V2,V3,V4,V5}和 9 条边的集合E={(v0,v1,5),(v1,v2,4),(v2,v3,9),(v3,v4,7),(v4,v0,1),(v0,v5,2),(v5,v4,8),(v3,v5,3),(v5,v2,1)}

　　上述示例图有助于说明两个其他关键图形术语：
　　路径 图中的路径是由边连接的顶点序列。形式上，我们将定义一个路径为 w1，w2，...，wn ，使得 (wi，wi + 1) ∈ E , 当 1≤i≤ n-1 。未加权路径长度是路径中的边的数目，具体是 n-1。加权路径长度是路径中所有边的权重的总和。例如在上图中，从 V3 到 V1 的路径是顶点序列 (V3，V4，V0，V1) 。边是 {（v3，v4,7），（v4，v0,1），（v0，v1,5）} } 。
　　循环 有向图中的循环是在同一顶点开始和结束的路径。例如，在 上图中，路径 （V5，V2，V3，V5） 是一个循环。没有循环的图形称为非循环图形。没有循环的有向图称为有向无环图或DAG 。我们将看到，如果问题可以表示为 DAG ，我们可以解决几个重要的问题。

2 图抽象数据类型

　图抽象数据类型（ADT）定义如下：

• Graph() 创建一个新的空图。
• addVertex(vert) 向图中添加一个顶点实例。
• addEdge(fromVert, toVert) 向连接两个顶点的图添加一个新的有向边。
• addEdge(fromVert, toVert, weight) 向连接两个顶点的图添加一个新的加权的有向边。
• getVertex(vertKey) 在图中找到名为 vertKey 的顶点。
• getVertices() 返回图中所有顶点的列表。
• in 返回 True 如果 vertex in graph 里给定的顶点在图中，否则返回False。

　　从图的正式定义开始，我们有几种方法可以在 Python 中实现图 ADT。 我们将看到在使用不同的表示来实现上述 ADT 时存在权衡。 有两个众所周知的图形、实现， 邻接矩阵 和 邻接表。 我们将解释这两个选项，然后实现一个作为 Python类。

3 邻接矩阵

　　实现图的最简单的方法之一是使用二维矩阵。在该矩阵实现中，每个行和列表示图中的顶点。存储在行 v 和列 w 的交叉点处的单元中的值表示是否存在从顶点 v 到顶点 w 的边。 当两个顶点通过边连接时，我们说它们是相邻的。 下图展示了 上图的邻接矩阵。单元格中的值表示从顶点 v 到顶点 w 的边的权重。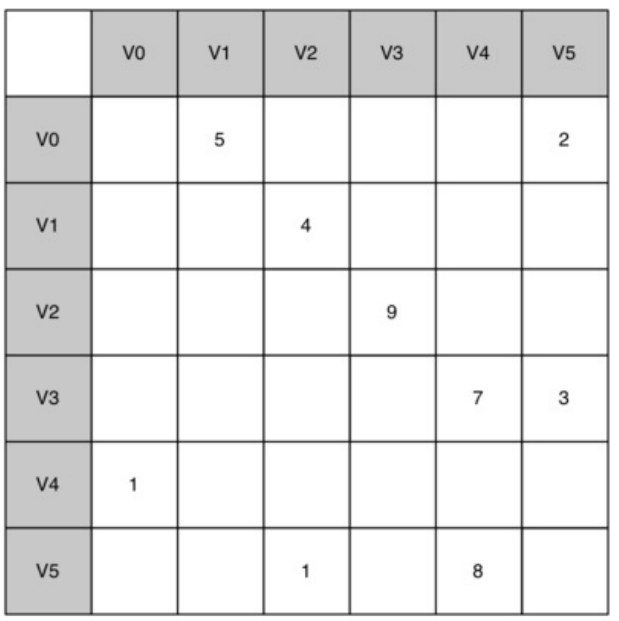

　　邻接矩阵的优点是简单，对于小图，很容易看到哪些节点连接到其他节点。 然而，注意矩阵中的大多数单元格是空的。 因为大多数单元格是空的，我们说这个矩阵是“稀疏的”。矩阵不是一种非常有效的方式来存储稀疏数据。 事实上，在Python中，你甚至要创建一个如 上图所示的矩阵结构。
　　当边的数量大时，邻接矩阵是图的良好实现。但是什么是大？填充矩阵需要多少边？ 由于图中每个顶点有一行和一列，填充矩阵所需的边数为 |V|^2。 当每个顶点连接到每个其他顶点时，矩阵是满的。有几个真实的问题，接近这种连接。 我们在本章中讨论的问题都涉及稀疏
连接的图。

4 邻接表

　　实现稀疏连接图的更空间高效的方法是使用邻接表。在邻接表实现中，我们保存Graph 对象中的所有顶点的主列表，然后图中的每个顶点对象维护连接到的其他顶点的列表。 在我们的顶点类的实现中，我们将使用字典而不是列表，其中字典键是顶点，值是权重。 下图展示了 第一张图的邻接列表示。

　　邻接表实现的优点是它允许我们紧凑地表示稀疏图。 邻接表还允许我们容易找到直接连接到特定顶点的所有链接。

5 实现

6 字梯的问题

7 构建字梯图

8 实现广度优先搜索

9 广度优先搜索分析

10 骑士之旅

11 构建骑士之旅图

12 实现气质之旅

13 骑士之旅分析

14 通用深度优先搜索

15 深度优先搜索分析

16 拓扑排序

17 强联通分量

18 最短路径问题

19 Dijkstra算法

20 Dijkstra算法分析

21 Prim生成树算法

22 总结