旋转数组的最小数字

题目描述

　　把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

 

算法设计思想

1. 暴力查找（Bruteforce Search）：把旋转数组从前到后遍历一遍，其时间复杂度为 O(n)。很明显，这种思想非常直接粗暴，没有用到旋转数组的性质。

2. 二分查找（Binary Search）：每次查找都把旋转数组平均分成两部分，通过比较当前旋转数组两端点和中间点的值，判断最小值在数组的哪一部分，从而达到缩小搜索范围的目的。其中，两端点为当前的旋转数组索引最小和索引最大的元素，中间点为这两部分子数组的连结元素，也可以看做为轴枢点（pivot point），这里取旋转数组的最小索引和最大索引的算术平均值（向下取整）作为索引，其对应的元素作为中间点。具体过程，如图 2.10 所示。

需要注意，当旋转数组的两端点的值都与中间点的值相等时，因为无法判断最小值在哪一部分，因此需要采用顺序查找方法，即暴力查找。其示例如图 2.11 所示。

 

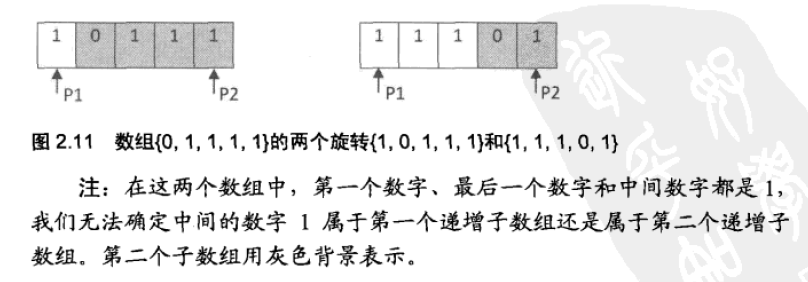
注意：

1）如果把排序数组的前面的0个元素搬到最后面，即排序数组本身，这仍是一个旋转数组，此时，数组中的第一个数字就是最小数字，可以直接返回，所以把中间元素mid初始化为0。

2）如果第一个指针指向的元素、第二个指针指向的元素和中间元素相同，则无法判断中间元素是属于哪个子数组，也就无法移动两个指针来缩小查找范围，此时还是要用顺序查找的方法。

class Solution:

    def minNumberInRotateArray(self, rotateArray):
        if len(rotateArray) == 0:
            return 0
        index1 = 0
        index2 = len(rotateArray)-1
        indexMid = index1

        while rotateArray[index1] >= rotateArray[index2]:
            if index2 - index1 == 1:
                indexMid = index2
                break
            indexMid = (index1 + index2) // 2

            def MinInorder(self, rotateArray, index1, index2):
                result = rotateArray[index1]
                for i in range(index1+1,index2+1):
                    if result > rotateArray[i]:
                        result = rotateArray[i]
                return result

            if rotateArray[index1] == rotateArray[index2] and rotateArray[indexMid] == rotateArray[index1]:
                return MinInorder(rotateArray,index1,index2)
            if rotateArray[indexMid] >= rotateArray[index1]:
                index1 = indexMid
            elif rotateArray[indexMid] <= rotateArray[index2]:
                index2 = indexMid
        return rotateArray[indexMid]