深度残差网络的理解

一说起“深度学习”，自然就联想到它非常显著的特点“深、深、深”（重要的事说三遍 ），通过很深层次的网络实现准确率非常高的图像识别、语音识别等能力。因此，我们自然很容易就想到：深的网络一般会比浅的网络效果好，如果要进一步地提升模型的准确率，最直接的方法就是把网络设计得越深越好，这样模型的准确率也就会越来越准确。

那现实真的是这样吗？

先看几个经典的图像识别深度学习模型： 

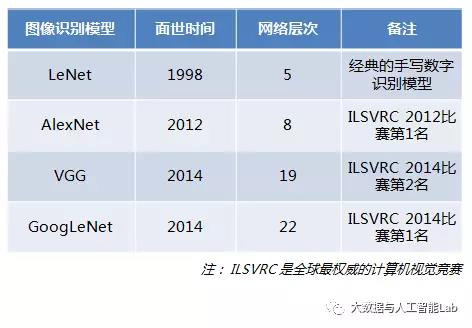
这几个模型都是在世界顶级比赛中获奖的著名模型，然而，一看这些模型的网络层次数量，似乎让人很失望，少则5层，多的也就22层而已，这些世界级模型的网络层级也没有那么深啊，这种也算深度学习吗？为什么不把网络层次加到成百上千层呢？

 

带着这个问题，我们先来看一个实验，对常规的网络（plain network，也称平原网络）直接堆叠很多层次，经对图像识别结果进行检验，训练集、测试集的误差结果如下图： 

 

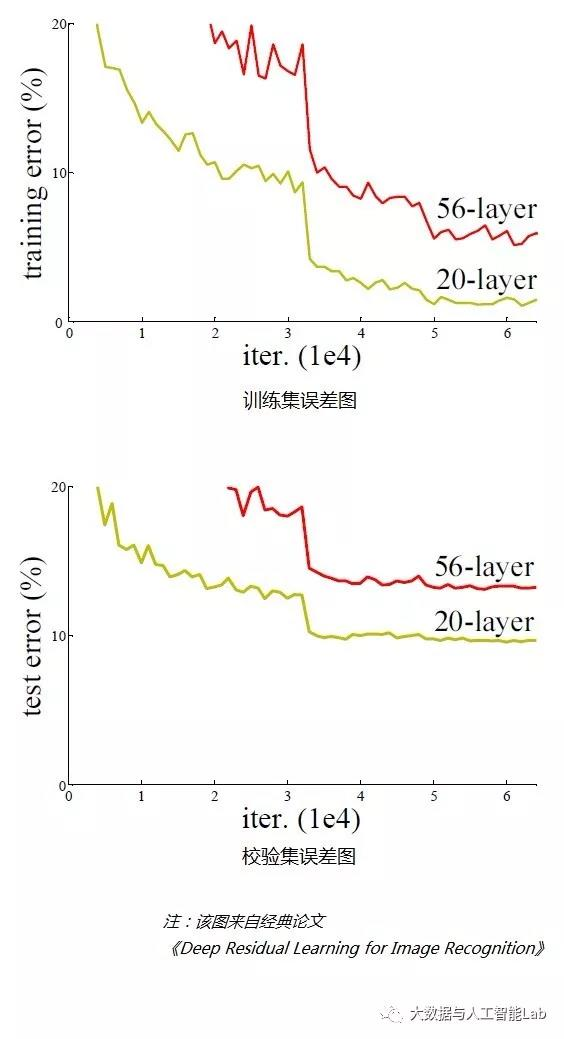
上面两个图可以看出，在网络很深的时候（56层相比20层），模型效果却越来越差了（误差率越高），并不是网络越深越好。

通过实验可以发现：随着网络层级的不断增加，模型精度不断得到提升，而当网络层级增加到一定的数目以后，训练精度和测试精度迅速下降，这说明当网络变得很深以后，深度网络就变得更加难以训练了。

【问题来了】为什么随着网络层级越深，模型效果却变差了呢？

 

下图是一个简单神经网络图，由输入层、隐含层、输出层构成： 

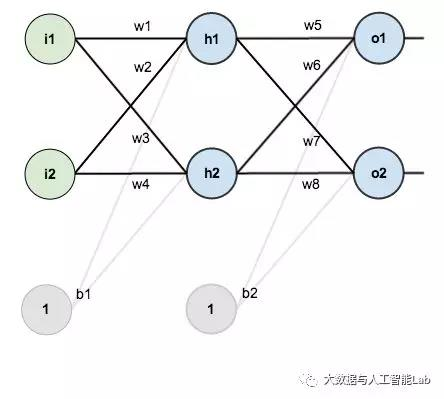
回想一下神经网络反向传播的原理，先通过正向传播计算出结果output，然后与样本比较得出误差值Etotal 

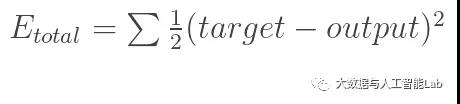
根据误差结果，利用著名的“链式法则”求偏导，使结果误差反向传播从而得出权重w调整的梯度。下图是输出结果到隐含层的反向传播过程（隐含层到输入层的反向传播过程也是类似）： 

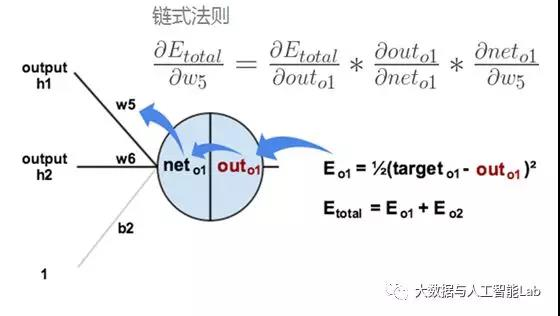
通过不断迭代，对参数矩阵进行不断调整后，使得输出结果的误差值更小，使输出结果与事实更加接近。

 

从上面的过程可以看出，神经网络在反向传播过程中要不断地传播梯度，而当网络层数加深时，梯度在传播过程中会逐渐消失（假如采用Sigmoid函数，对于幅度为1的信号，每向后传递一层，梯度就衰减为原来的0.25，层数越多，衰减越厉害），导致无法对前面网络层的权重进行有效的调整。

 

那么，如何又能加深网络层数、又能解决梯度消失问题、又能提升模型精度呢？

 

【主角登场】深度残差网络（Deep Residual Network，简称DRN）

 

前面描述了一个实验结果现象，在不断加神经网络的深度时，模型准确率会先上升然后达到饱和，再持续增加深度时则会导致准确率下降，示意图如下： 

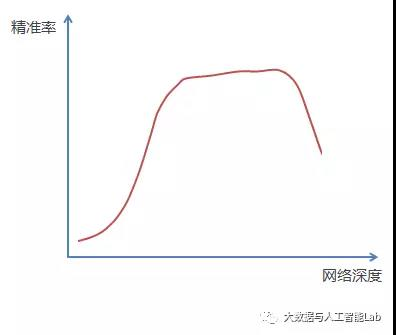
那么我们作这样一个假设：假设现有一个比较浅的网络（Shallow Net）已达到了饱和的准确率，这时在它后面再加上几个恒等映射层（Identity mapping，也即y=x，输出等于输入），这样就增加了网络的深度，并且起码误差不会增加，也即更深的网络不应该带来训练集上误差的上升。而这里提到的使用恒等映射直接将前一层输出传到后面的思想，便是著名深度残差网络ResNet的灵感来源。

 

ResNet引入了残差网络结构（residual network），通过这种残差网络结构，可以把网络层弄的很深（据说目前可以达到1000多层），并且最终的分类效果也非常好，残差网络的基本结构如下图所示，很明显，该图是带有跳跃结构的：

 

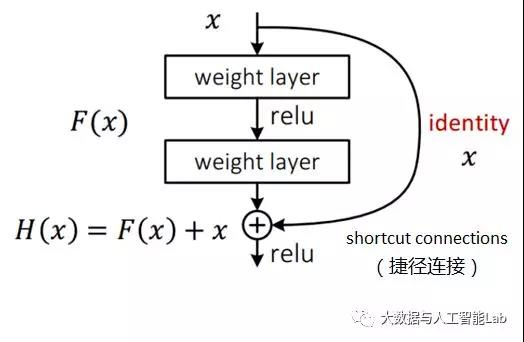
残差网络借鉴了高速网络（Highway Network）的跨层链接思想，但对其进行改进（残差项原本是带权值的，但ResNet用恒等映射代替之）。

假定某段神经网络的输入是x，期望输出是H(x)，即H(x)是期望的复杂潜在映射，如果是要学习这样的模型，则训练难度会比较大；

回想前面的假设，如果已经学习到较饱和的准确率（或者当发现下层的误差变大时），那么接下来的学习目标就转变为恒等映射的学习，也就是使输入x近似于输出H(x)，以保持在后面的层次中不会造成精度下降。

在上图的残差网络结构图中，通过“shortcut connections（捷径连接）”的方式，直接把输入x传到输出作为初始结果，输出结果为H(x)=F(x)+x，当F(x)=0时，那么H(x)=x，也就是上面所提到的恒等映射。于是，ResNet相当于将学习目标改变了，不再是学习一个完整的输出，而是目标值H(X)和x的差值，也就是所谓的残差F(x) := H(x)-x，因此，后面的训练目标就是要将残差结果逼近于0，使到随着网络加深，准确率不下降。

这种残差跳跃式的结构，打破了传统的神经网络n-1层的输出只能给n层作为输入的惯例，使某一层的输出可以直接跨过几层作为后面某一层的输入，其意义在于为叠加多层网络而使得整个学习模型的错误率不降反升的难题提供了新的方向。

至此，神经网络的层数可以超越之前的约束，达到几十层、上百层甚至千层，为高级语义特征提取和分类提供了可行性。

 

下面感受一下34层的深度残差网络的结构图，是不是很壮观：

 

因为经过“shortcut connections（捷径连接）”后，H(x)=F(x)+x，如果F(x)和x的通道相同，则可直接相加，那么通道不同怎么相加呢。上图中的实线、虚线就是为了区分这两种情况的：

  • 实线的Connection部分，表示通道相同，如上图的第一个粉色矩形和第三个粉色矩形，都是3x3x64的特征图，由于通道相同，所以采用计算方式为H(x)=F(x)+x

  • 虚线的的Connection部分，表示通道不同，如上图的第一个绿色矩形和第三个绿色矩形，分别是3x3x64和3x3x128的特征图，通道不同，采用的计算方式为H(x)=F(x)+Wx，其中W是卷积操作，用来调整x维度的。

 

除了上面提到的两层残差学习单元，还有三层的残差学习单元，如下图所示： 

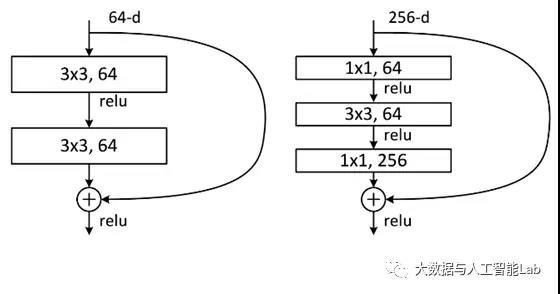
两种结构分别针对ResNet34（左图）和ResNet50/101/152（右图），其目的主要就是为了降低参数的数目。左图是两个3x3x256的卷积，参数数目: 3x3x256x256x2 = 1179648，右图是第一个1x1的卷积把256维通道降到64维，然后在最后通过1x1卷积恢复，整体上用的参数数目：1x1x256x64 + 3x3x64x64 + 1x1x64x256 = 69632，右图的参数数量比左图减少了16.94倍，因此，右图的主要目的就是为了减少参数量，从而减少计算量。

对于常规的ResNet，可以用于34层或者更少的网络中（左图）；对于更深的网络（如101层），则使用右图，其目的是减少计算和参数量。

 

经检验，深度残差网络的确解决了退化问题，如下图所示，左图为平原网络（plain network）网络层次越深（34层）比网络层次浅的（18层）的误差率更高；右图为残差网络ResNet的网络层次越深（34层）比网络层次浅的（18层）的误差率更低。 

 

结语

ResNet在ILSVRC2015竞赛中惊艳亮相，一下子将网络深度提升到152层，将错误率降到了3.57，在图像识别错误率和网络深度方面，比往届比赛有了非常大的提升，ResNet毫无悬念地夺得了ILSVRC2015的第一名。如下图所示： 

在ResNet的作者的第二篇相关论文《Identity Mappings in Deep Residual Networks》中，提出了ResNet V2。ResNet V2 和 ResNet V1 的主要区别在于，作者通过研究 ResNet 残差学习单元的传播公式，发现前馈和反馈信号可以直接传输，因此“shortcut connection”（捷径连接）的非线性激活函数（如ReLU）替换为 Identity Mappings。同时，ResNet V2 在每一层中都使用了 Batch Normalization。这样处理后，新的残差学习单元比以前更容易训练且泛化性更强。

参考

 

posted @ 2018-07-13 15:56  耐烦不急  阅读(7027)  评论(0)  编辑  收藏  举报