神经网络
神经网络
初始神经网络：
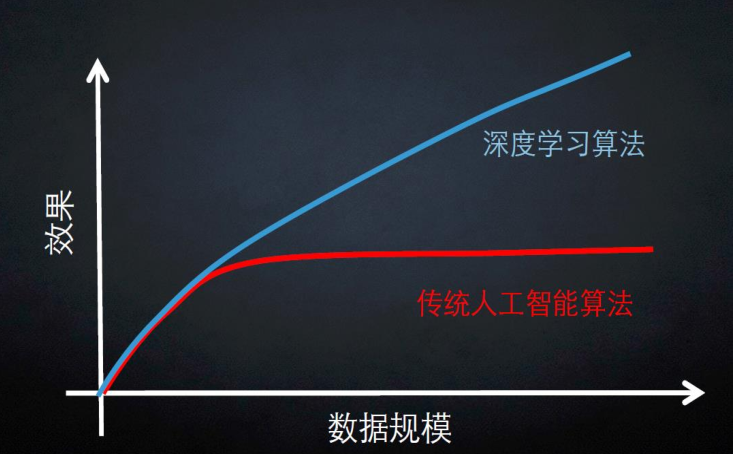
计算机视觉所面临的挑战：
K近邻尝试图像分类：
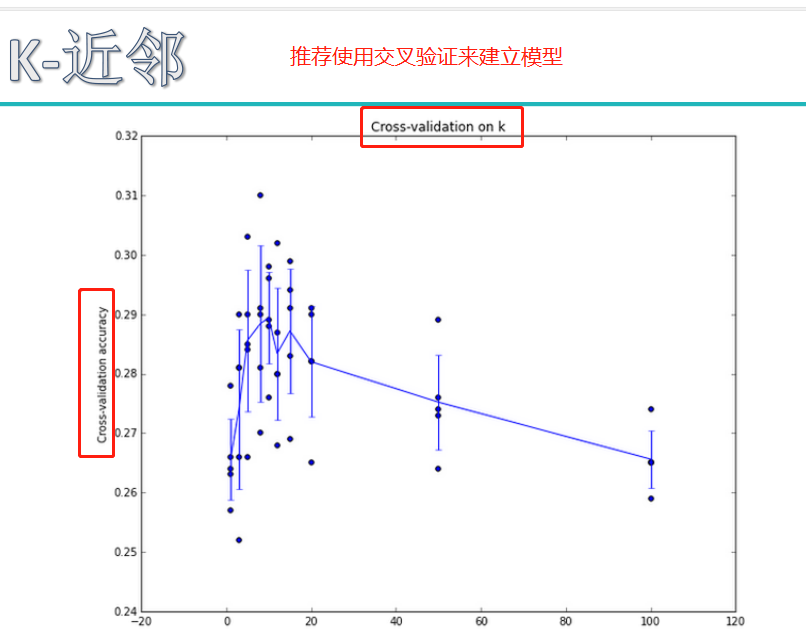
超参数的作用：
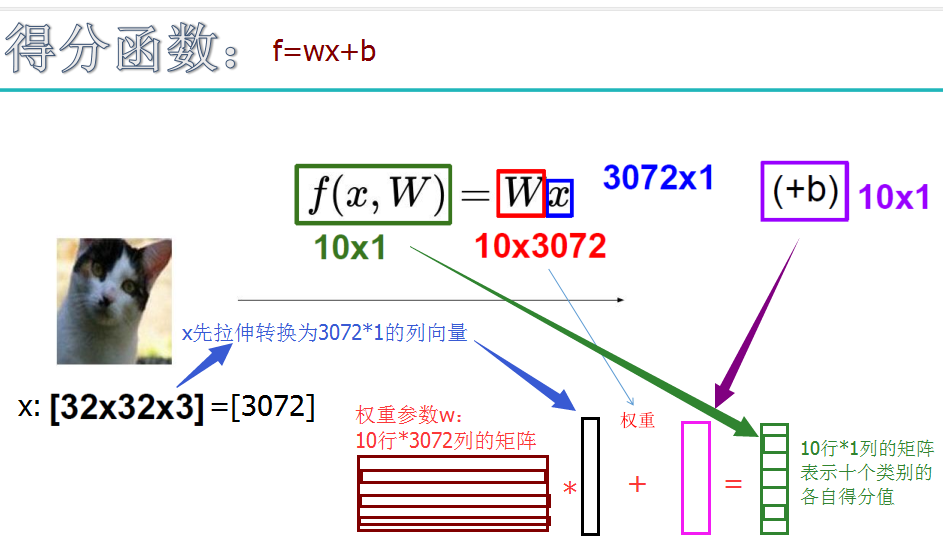
线性分类原理：
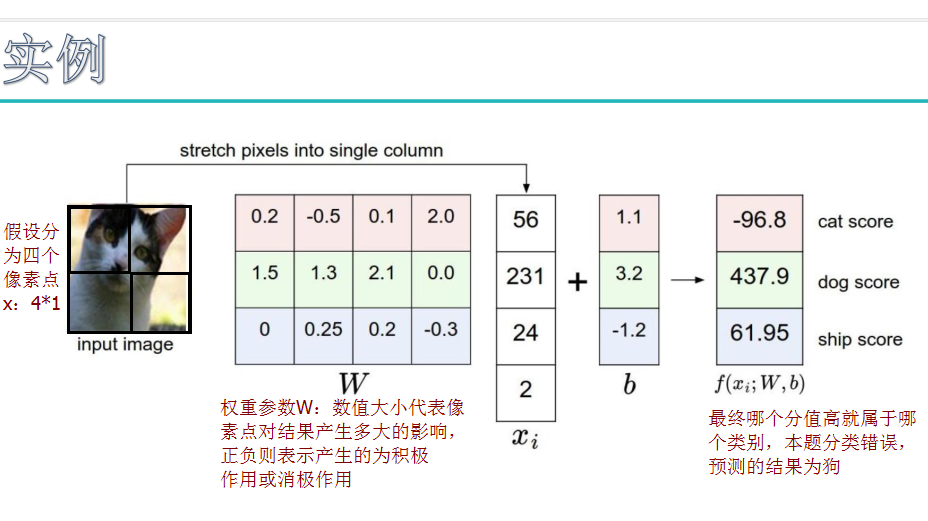
损失函数：
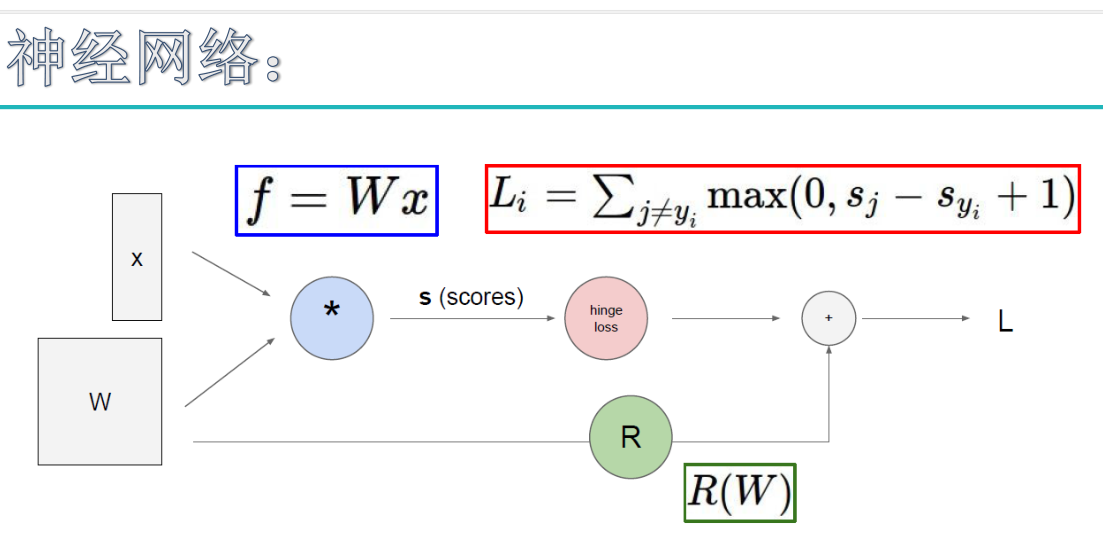
这里的损失函数同svm损失函数，hinge损失函数。
score for correct class-score for other classes>>delta,预测结果越好。score越大越好
为了得到w2这种模型，加入正则化惩罚项
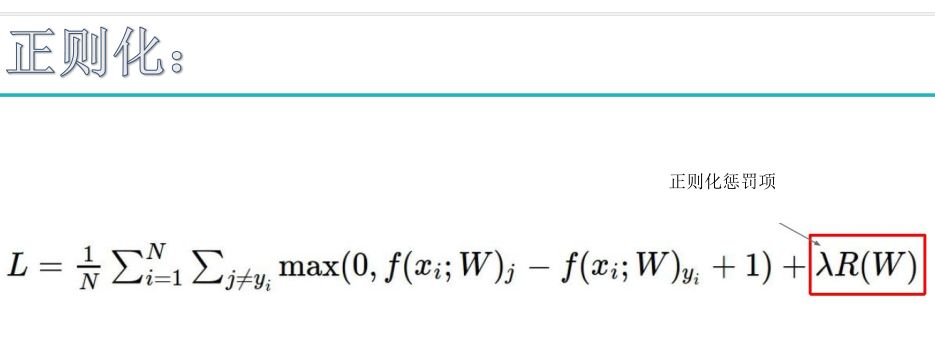
正则化惩罚项是惩罚权重参数的。
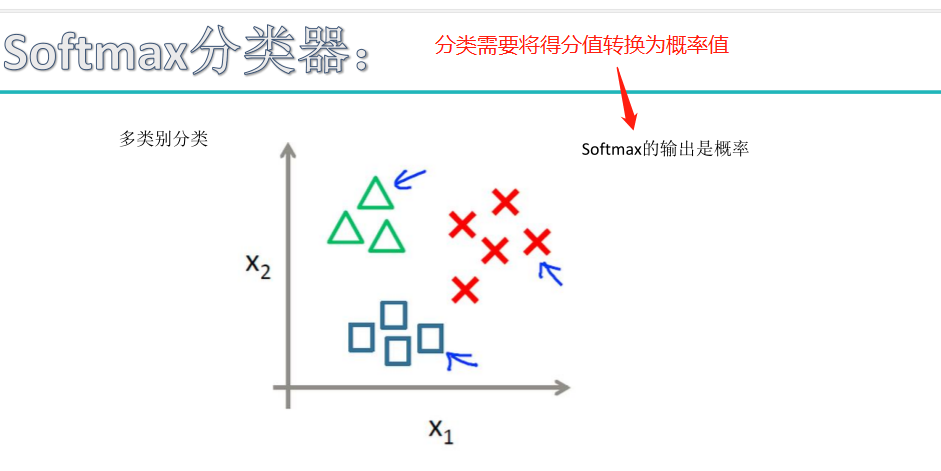
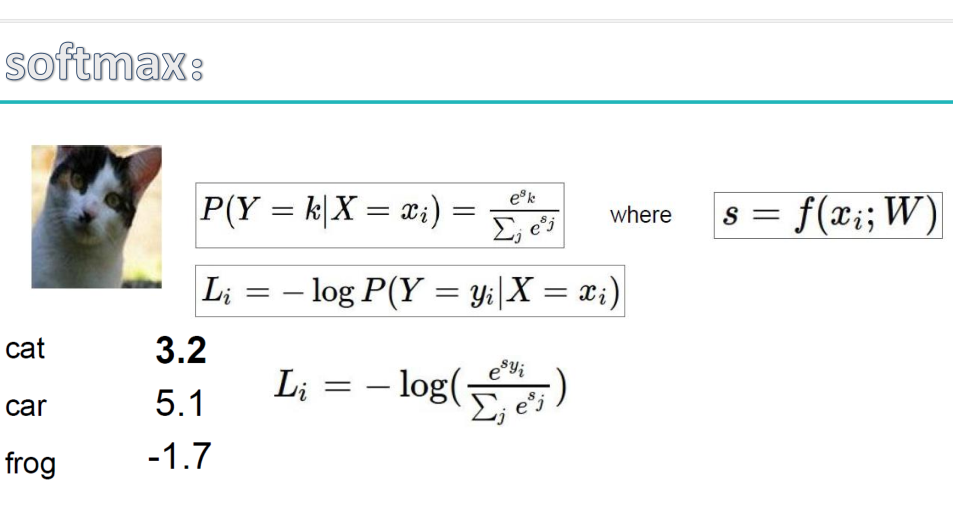
面试必考，SVM和SoftMax的原理区别对比,点击查看
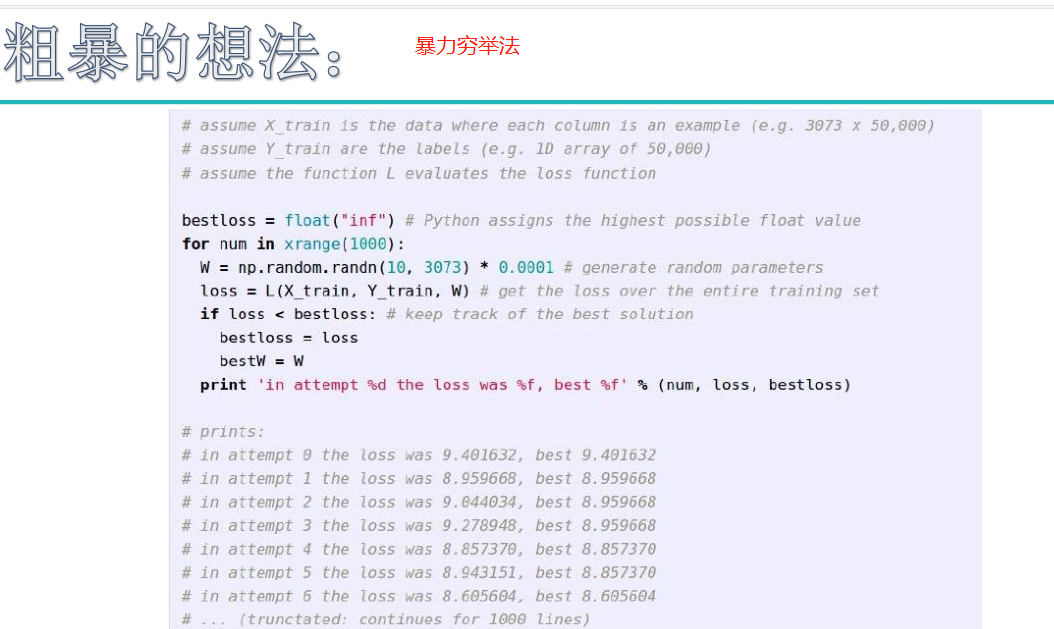
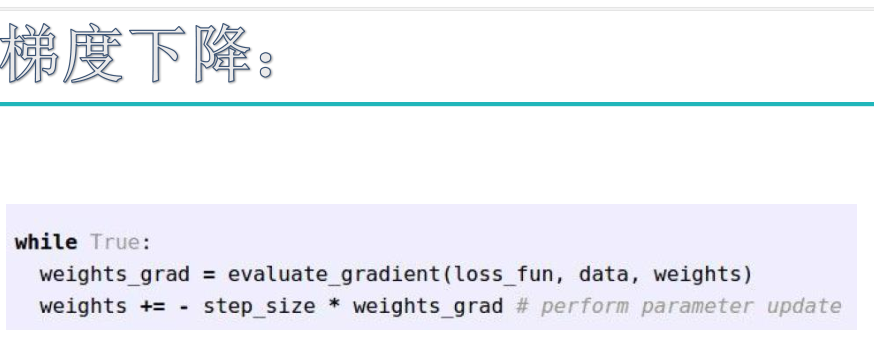
在深度学习中，经常要设置以下几个数据：nEpoch , iteration , batchSIze:
batchSize 代表在做随机梯度下降时，使用批梯度的数量，即每次使用batchSize个数据来更新参数。
1个iteration等于使用batchSize个样本训练一次
1个nEpoch等于使用所有样本训练一次
举个例子，训练集有1000个样本，batchsize=10，那么：
训练完整个样本集需要：
100次iteration，1次epoch。
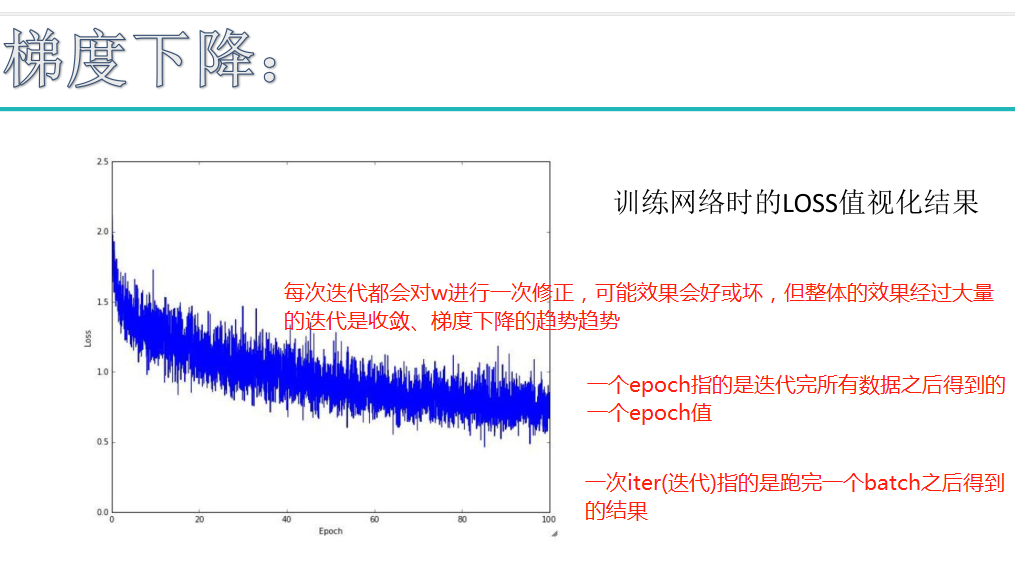
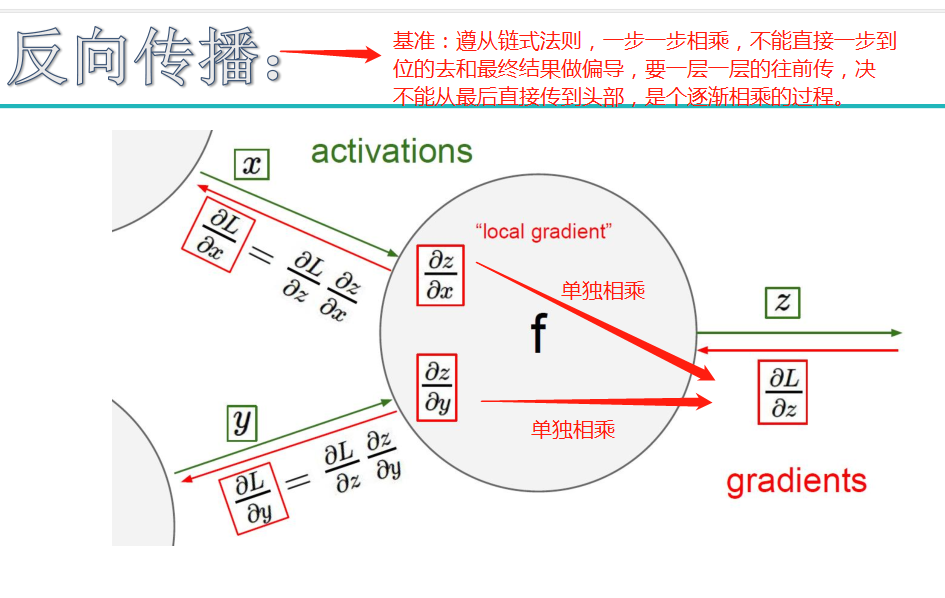
补充：一次iter（迭代）指的是跑完一个batch的前向传播和反向传播的过程；反向传播是为了调整权重参数w
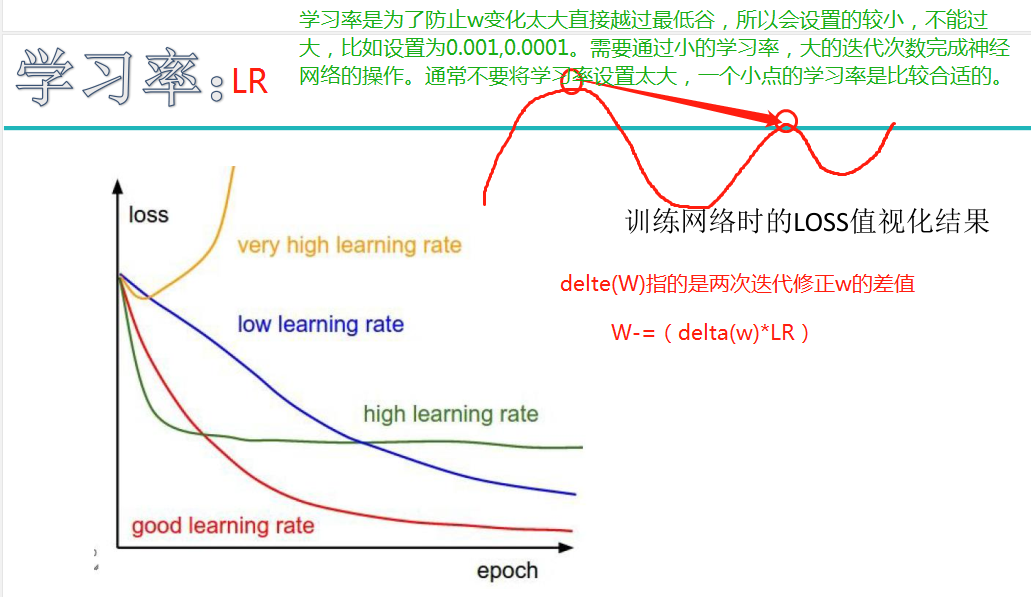
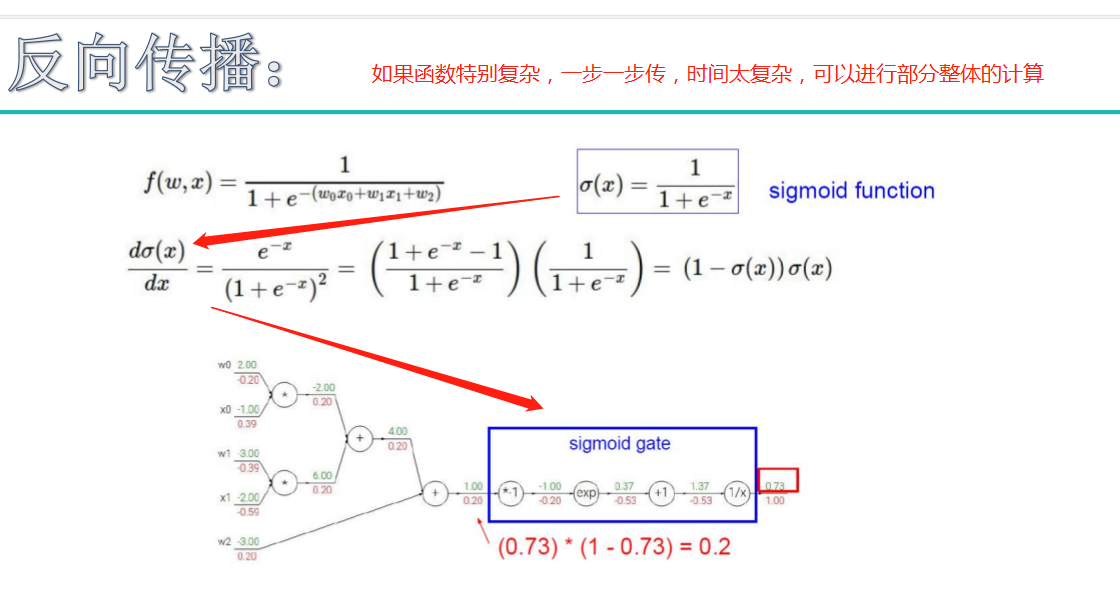
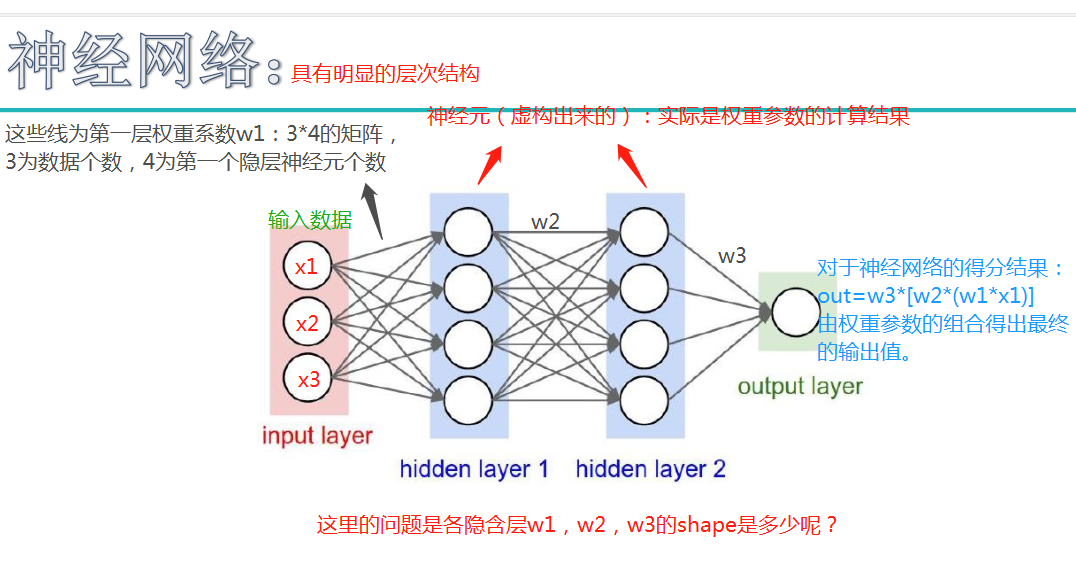注：最后的蓝色公式中，w1*x1改为w1*x
另一个问题：为什么要用隐层？
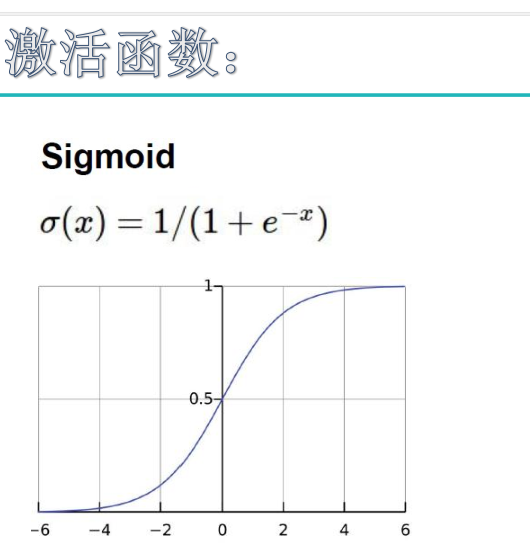
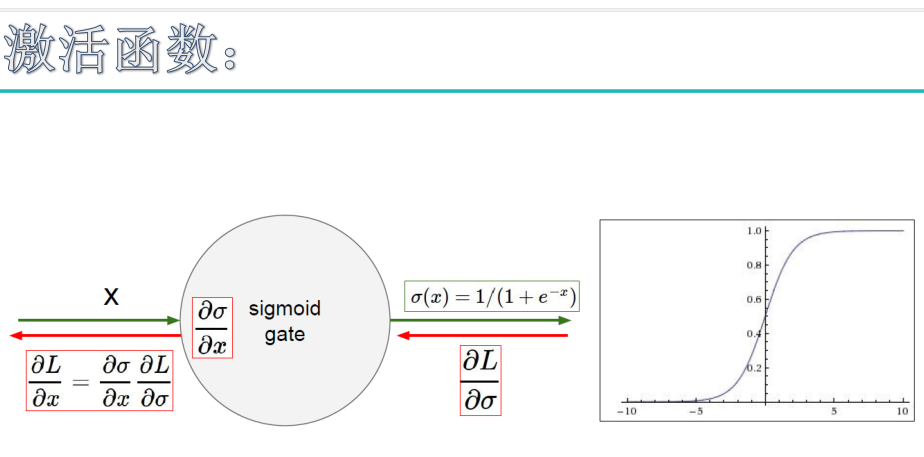
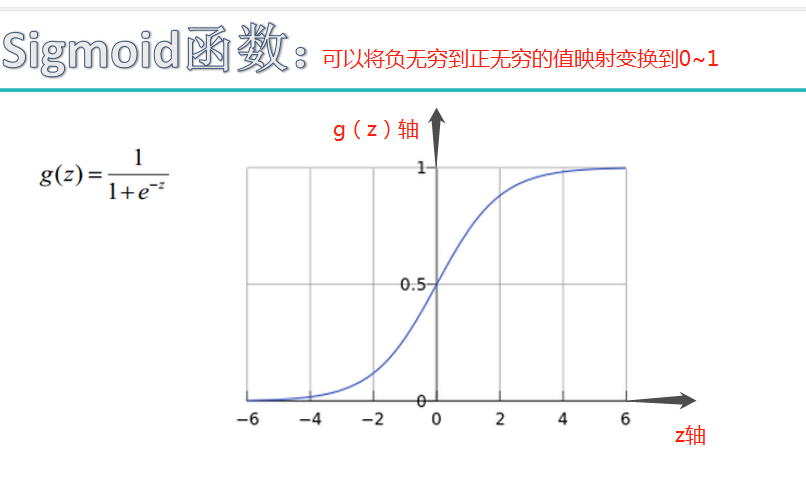
sigmoid函数也叫 Logistic 函数，用于隐层神经元输出
取值范围为(0,1)
它可以将一个实数映射到(0,1)的区间，可以用来做二分类。
在特征相差比较复杂或是相差不是特别大时效果比较好。
sigmoid缺点：
激活函数计算量大，反向传播求误差梯度时，求导涉及除法
反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练
下面解释为何会出现梯度消失：
反向传播算法中，要对激活函数求导，sigmoid 的导数表达式为：
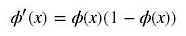
sigmoid 原函数及导数图形如下：
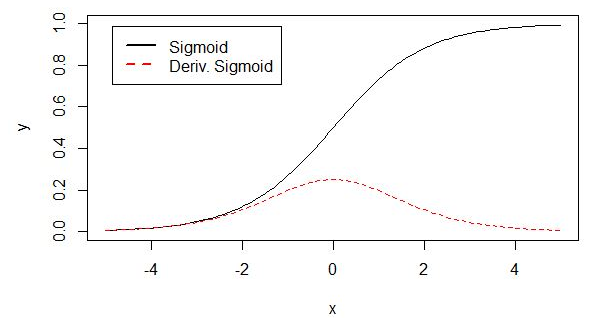
由图可知，导数从 0 开始很快就又趋近于 0 了，易造成“梯度消失”现象，就无法做反向传播，神经网络就不会收敛，所以在深度学习中已经把sigmoid函数淘汰了。
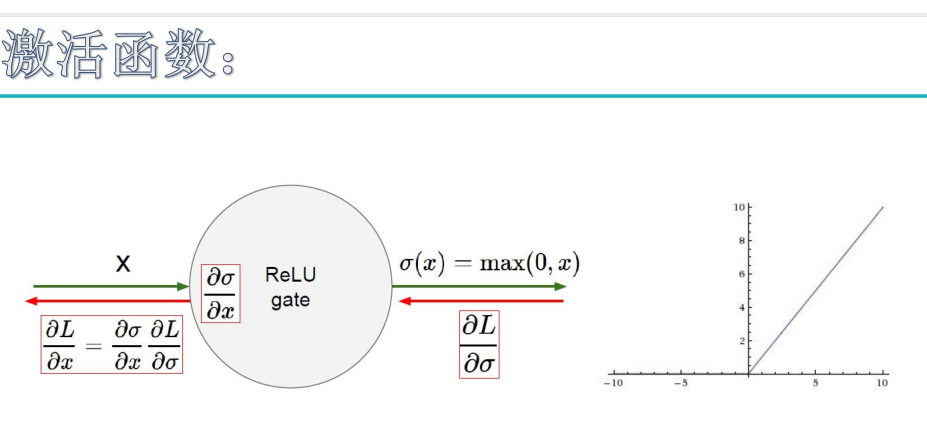
输入信号 <0 时，输出都是0，>0 的情况下，输出等于输入
ReLU 的优点：
Krizhevsky et al. 发现使用 ReLU 得到的 SGD（随机梯度下降） 的收敛速度会比 sigmoid/tanh 快很多。另外解决梯度消失问题，并且求导简单。
ReLU激活函数已经是当前神经网络激活函数的首选与默认选择了。
神经网络过拟合解决方案：
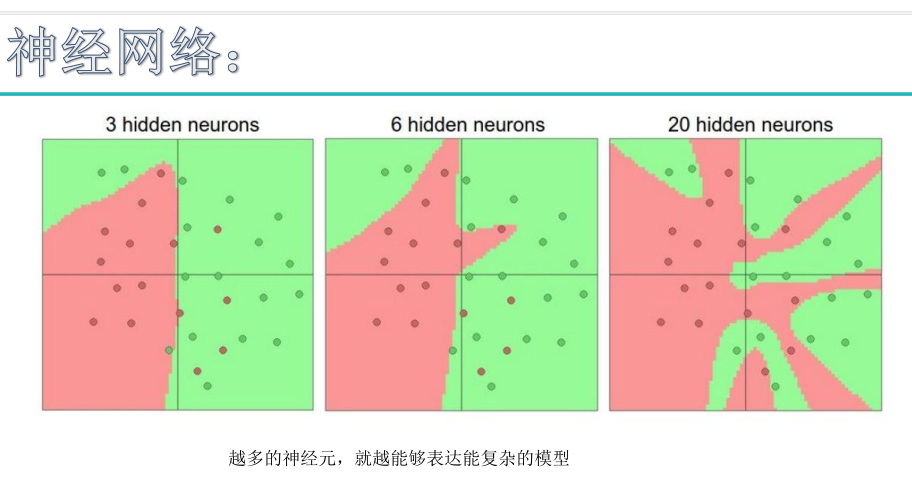
神经元数量越多，当前神经网络效果越好，但是越容易发生过拟合。神经网络最大的特点是非常容易发生过拟合现象。
神经网络内部没办法可视化展示，只能通过整体的逻辑来说明神经网络是做的什么事情，无法解释w1，w2，w3.。。。究竟是为什么这么设置的，以及他们之间的关系是怎样的，以及关系表达的是什么。
神经网络泛化能力强才能发挥其作用。
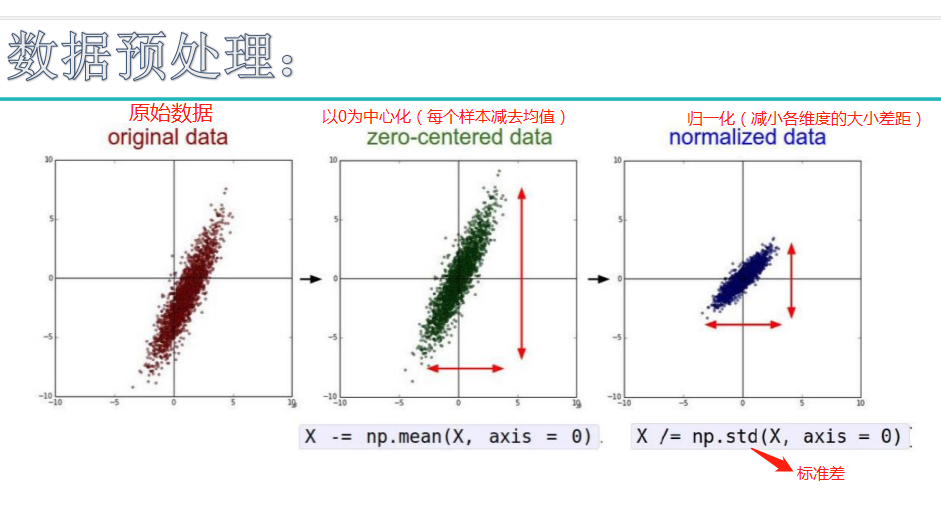
例如：图像数据在0~255之间，压缩到0~1范围（-=mean操作），再除以标准差，得到归一化的数据，所有值在0~1之间。
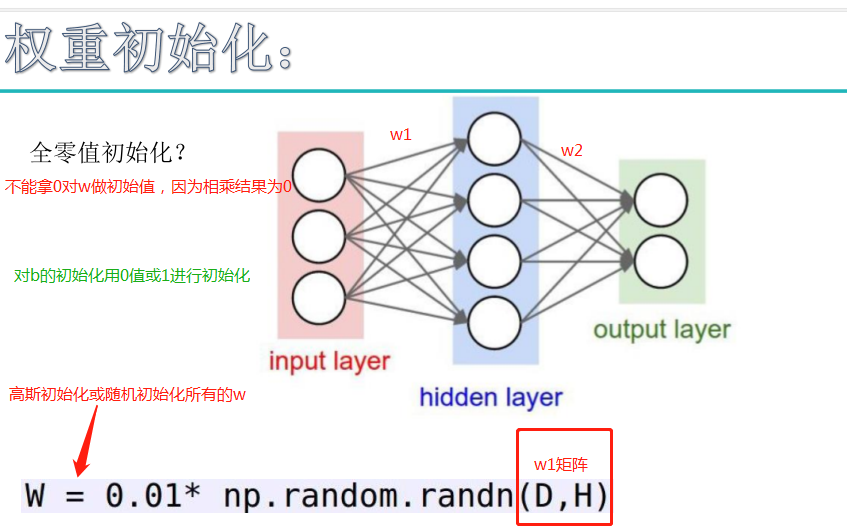
注：对w不能常值初始化（全设置成固定值），如果常值初始化则会沿着一个方向更新，或者干脆不更新。b对最终结果影响很小，对b值要常值初始化。
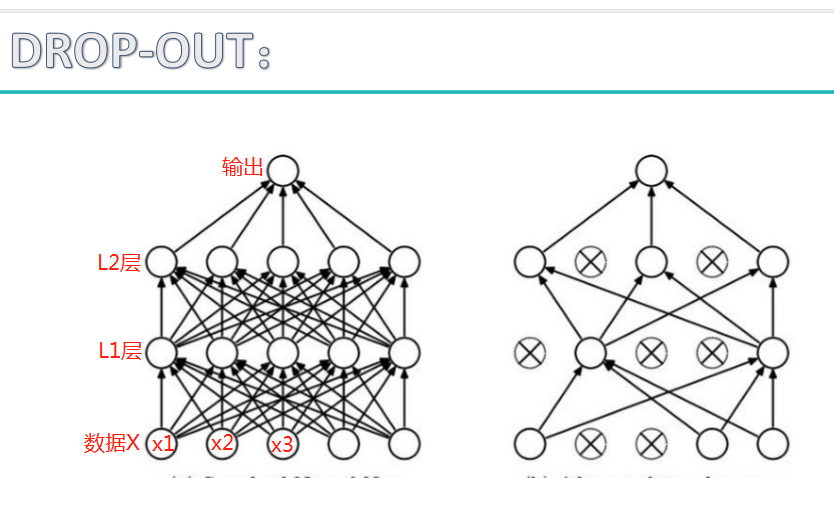
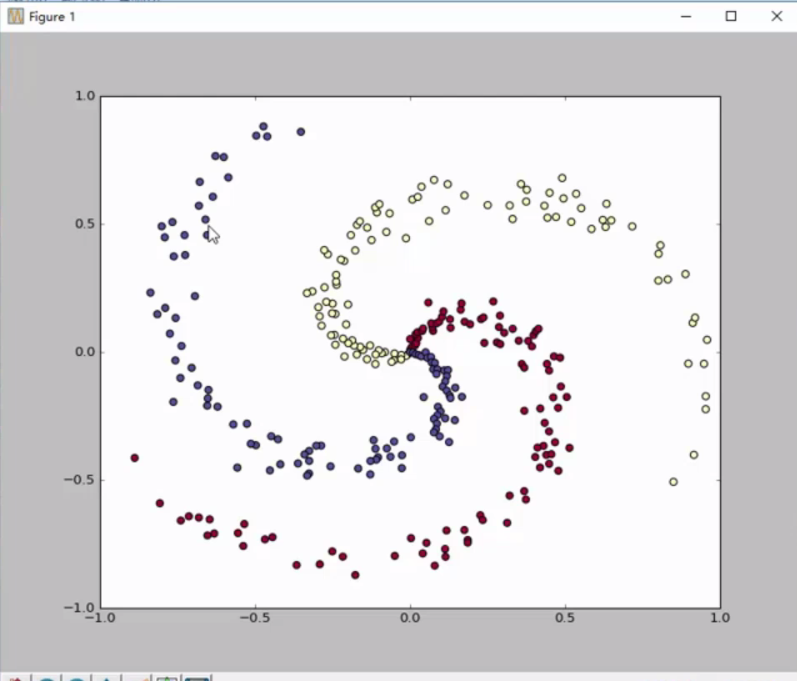
感受神经网络的强大
#Train a Linear Classifier 线性分类器
import numpy as np
import matplotlib.pyplot as plt
#构造数据，三类样本点，每类样本点有100个
np.random.seed(0)
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D))
y = np.zeros(N*K, dtype='uint8')
for j in range(K):
ix = range(N*j,N*(j+1))
r = np.linspace(0.0,1,N) # radius
t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
y[ix] = j
#初始化w和b
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))
# some hyperparameters 正则化惩罚项
step_size = 1e-0
reg = 1e-3 # regularization strength
# gradient descent loop
num_examples = X.shape[0]
for i in range(1000):#循环迭代，前向传播
#print X.shape
# evaluate class scores, [N x K]
scores = np.dot(X, W) + b #x:300*2 scores:300*3 得分值=wx+b
#print scores.shape
# compute the class probabilities 得分值归一化操作，将其转化为概率值
exp_scores = np.exp(scores)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K] probs:300*3
print(probs.shape)
# compute the loss: average cross-entropy loss and regularization
corect_logprobs = -np.log(probs[range(num_examples),y]) #corect_logprobs:300*1 计算loss值，开始反向传播
print(corect_logprobs.shape)
data_loss = np.sum(corect_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss
if i % 100 == 0:
print("iteration %d: loss %f" % (i, loss))
# compute the gradient on scores
dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples
# backpropate the gradient to the parameters (W,b)
dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # regularization gradient
# perform a parameter update
W += -step_size * dW
b += -step_size * db
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print('training accuracy: %.2f' % (np.mean(predicted_class == y)))
h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()
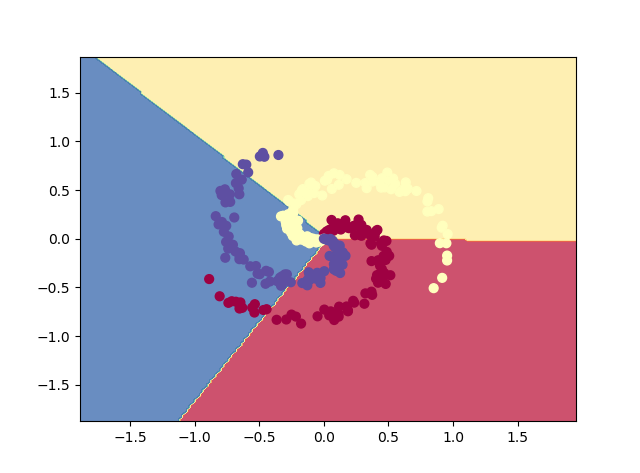
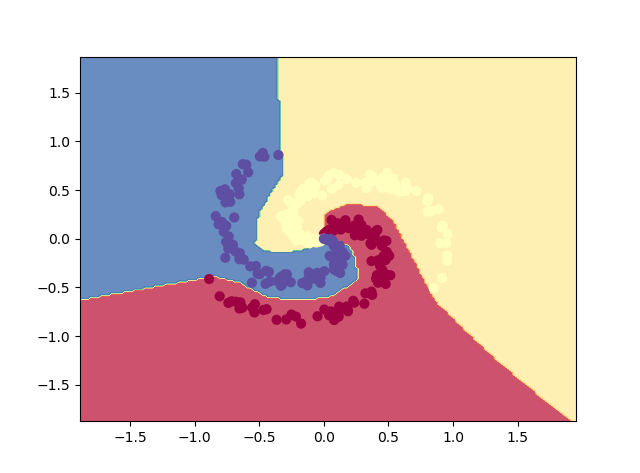
#线性操作在环状数据集上没办法表现好
结果：
D:\Anaconda3\python.exe C:/Users/Administrator/Desktop/py_work/linerCla.py (300, 3) (300,) iteration 0: loss 1.096919 (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) iteration 100: loss 0.787937 (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) iteration 200: loss 0.786281 (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) iteration 300: loss 0.786231 (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) iteration 400: loss 0.786230 (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) (300, 3) (300,) iteration 500: loss 0.786230 iteration 600: loss 0.786230 iteration 700: loss 0.786230 iteration 800: loss 0.786230 iteration 900: loss 0.786230 training accuracy: 0.49
#Train a Linear Classifier 线性分类器
import numpy as np
import matplotlib.pyplot as plt
#构造数据，三类样本点，每类样本点有100个
np.random.seed(0)
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
X = np.zeros((N*K,D))
y = np.zeros(N*K, dtype='uint8')
for j in range(K):
ix = range(N*j,N*(j+1))
r = np.linspace(0.0,1,N) # radius
t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
y[ix] = j
#初始化w和b
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))
# some hyperparameters 正则化惩罚项
step_size = 1e-0
reg = 1e-3 # regularization strength
# gradient descent loop
num_examples = X.shape[0]
for i in range(1000):#循环迭代，前向传播
#print X.shape
# evaluate class scores, [N x K]
scores = np.dot(X, W) + b #x:300*2 scores:300*3 得分值=wx+b
#print scores.shape
# compute the class probabilities 得分值归一化操作，将其转化为概率值
exp_scores = np.exp(scores)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K] probs:300*3
print(probs.shape)
# compute the loss: average cross-entropy loss and regularization
corect_logprobs = -np.log(probs[range(num_examples),y]) #corect_logprobs:300*1 计算loss值，开始反向传播
print(corect_logprobs.shape)
data_loss = np.sum(corect_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss
if i % 100 == 0:
print("iteration %d: loss %f" % (i, loss))
# compute the gradient on scores
dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples
# backpropate the gradient to the parameters (W,b)
dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # regularization gradient
# perform a parameter update
W += -step_size * dW
b += -step_size * db
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print('training accuracy: %.2f' % (np.mean(predicted_class == y)))
h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()
#线性操作在环状数据集上没办法表现好
结果：
D:\Anaconda3\python.exe C:/Users/Administrator/Desktop/py_work/NNCla.py iteration 0: loss 1.098765 iteration 100: loss 0.723927 iteration 200: loss 0.697608 iteration 300: loss 0.587562 iteration 400: loss 0.426585 iteration 500: loss 0.357190 iteration 600: loss 0.349933 iteration 700: loss 0.346522 iteration 800: loss 0.336137 iteration 900: loss 0.309860 iteration 1000: loss 0.292278 iteration 1100: loss 0.284574 iteration 1200: loss 0.275849 iteration 1300: loss 0.271355 iteration 1400: loss 0.267756 iteration 1500: loss 0.265369 iteration 1600: loss 0.262948 iteration 1700: loss 0.260838 iteration 1800: loss 0.259226 iteration 1900: loss 0.257831 training accuracy: 0.97
注：本图为传统神经网络的四个步骤。
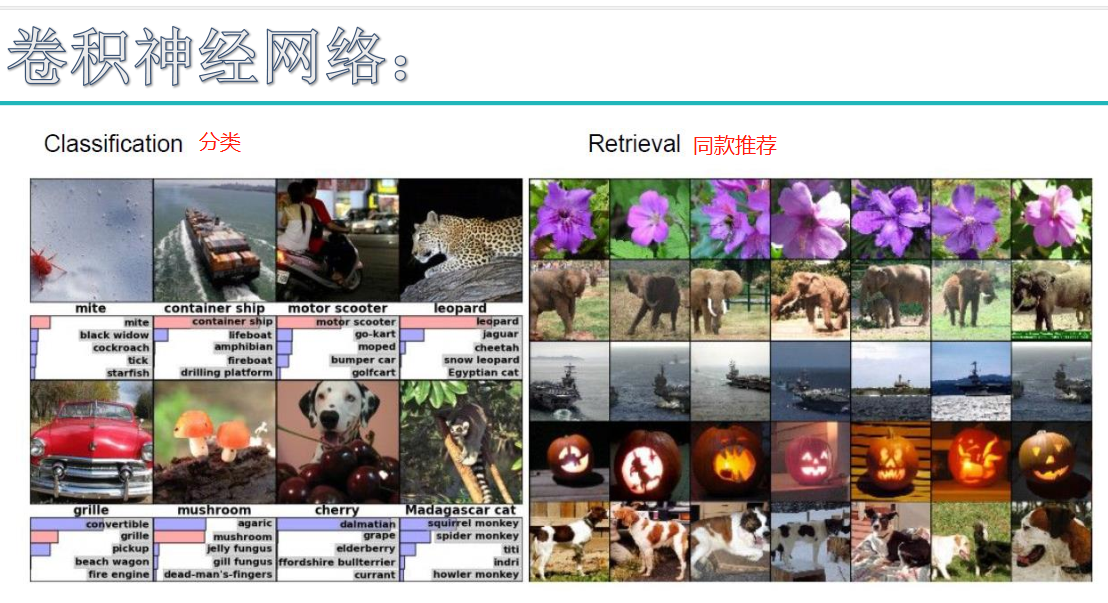
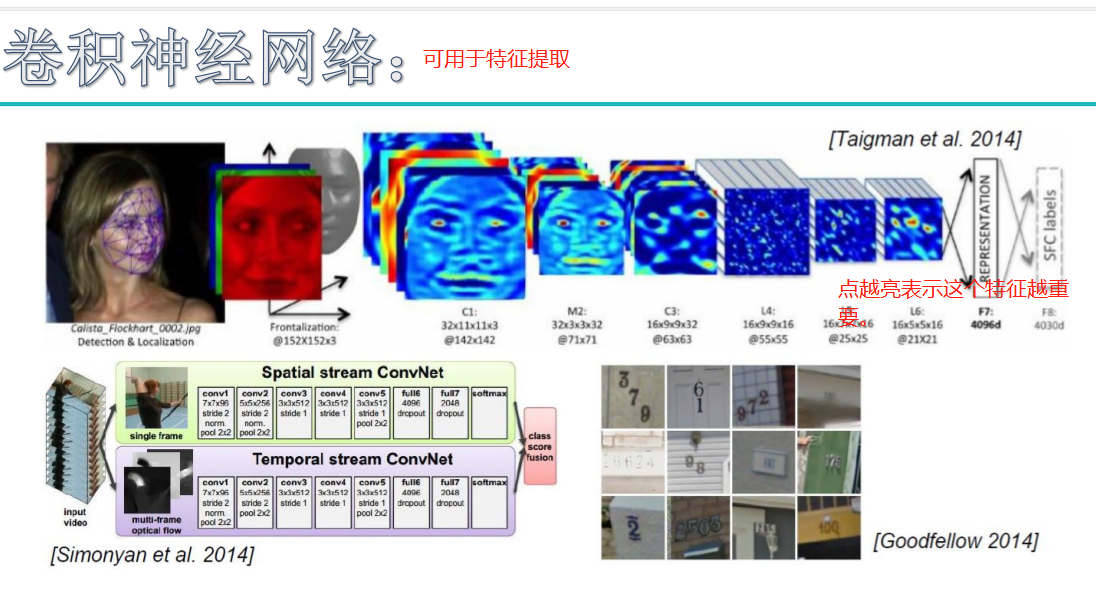
卷积层详解：
卷积神经网络（CNN）由输入层、卷积层、激活函数、池化层、全连接层组成，即INPUT-CONV-RELU-POOL-FC
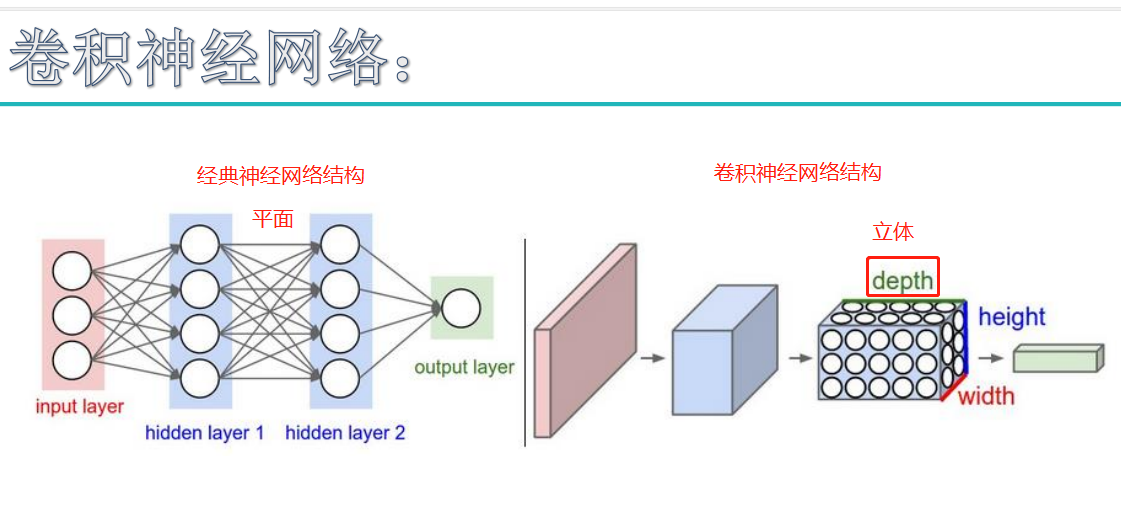
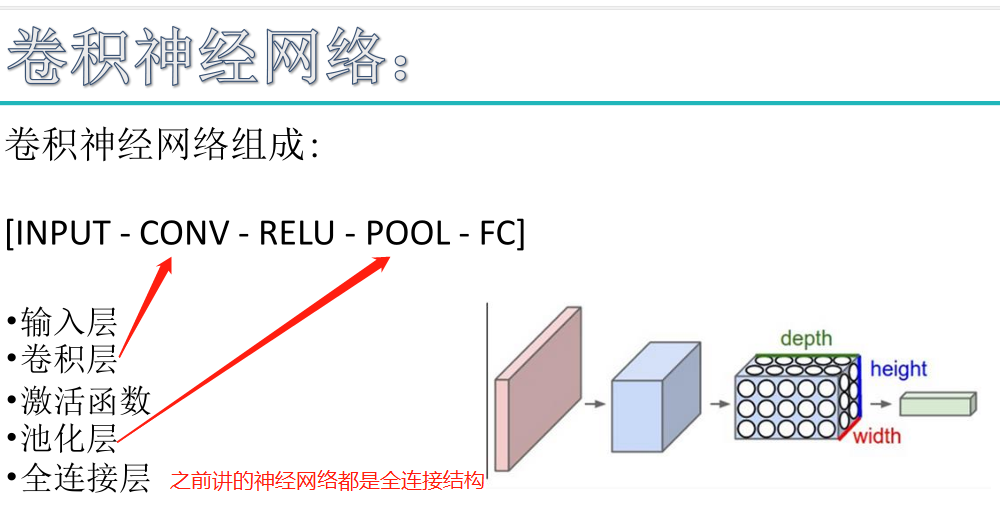
卷积层：用它来进行特征提取，如下：
注：不是fifter，是filter
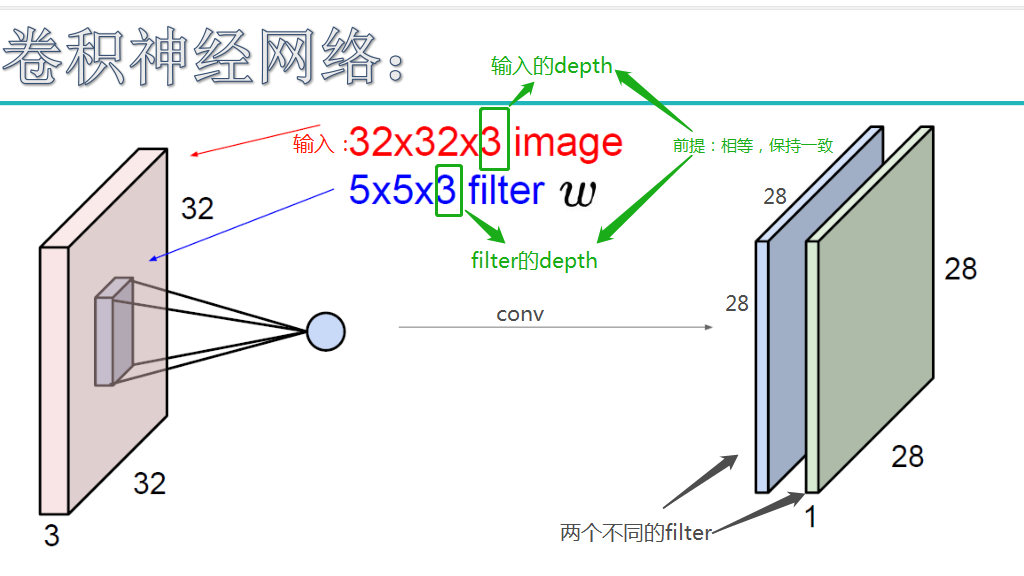
输入图像是32*32*3，3是它的深度（即R、G、B），卷积层是一个5*5*3的filter(感受野)，这里注意：感受野的深度必须和输入图像的深度相同。通过一个filter与输入图像的卷积可以得到一个28*28*1的特征图，上图是用了两个filter得到了两个特征图；
我们通常会使用多层卷积层来得到更深层次的特征图。如下：
卷积层
卷积层从原输入的三维版本开始，一般是包括色彩、宽度、高度三维的图像。接着，图像被分解为过滤器（核）的子集，每个过滤器的感受野均小于图像总体。这些过滤器接着沿着输入量的宽高应用卷积，计算过滤器项和输入的点积，并生成过滤器的二维激活映射。这使得网络学习因为侦测到输入的空间位置上特定种类的特征而激活的过滤器。过滤器沿着整个图像进行“扫描”，这让CNN具有平移不变性，也就是说，CNN可以处理位于图像不同部分的物体。
接着叠加激活函数，这构成卷积层输出的深度。输出量中的每一项因此可以视作查看输入的一小部分的神经元的输出，同一激活映射中的神经元共享参数。
卷积层的一个关键概念是局部连通性，每个神经元仅仅连接到输入量中的一小部分。过滤器的尺寸，也称为感受野，是决定连通程度的关键因素。
其他关键参数是深度、步长、补齐。深度表示创建的特征映射数目。步长控制每个卷积核在图像上移动的步幅。一般将步长设为1，从而导向高度重叠的感受野和较大的输出量。补齐让我们可以控制输出量的空间大小。如果我们用零补齐（zero-padding），它能提供和输入量等高等宽的输出。
卷积计算流程：
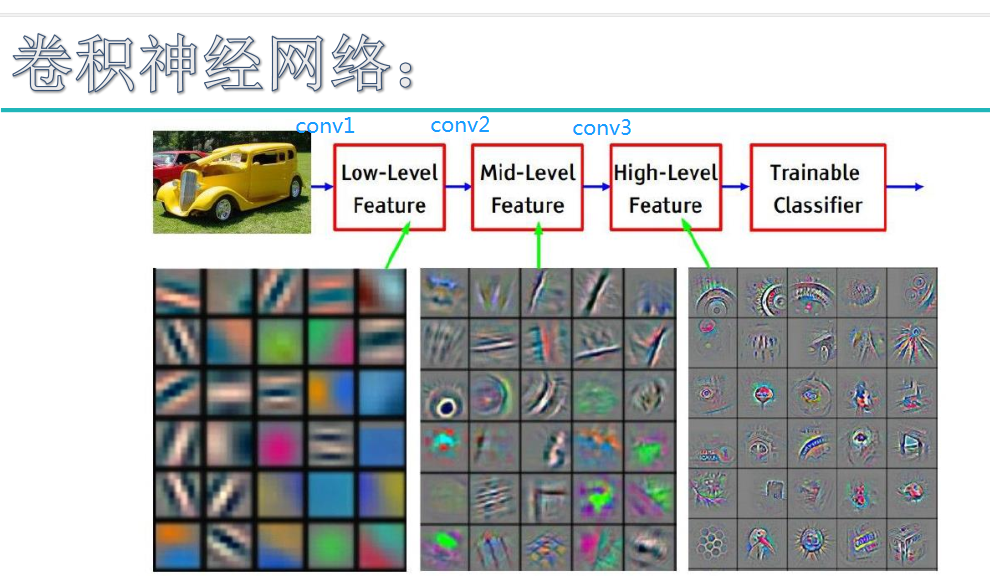
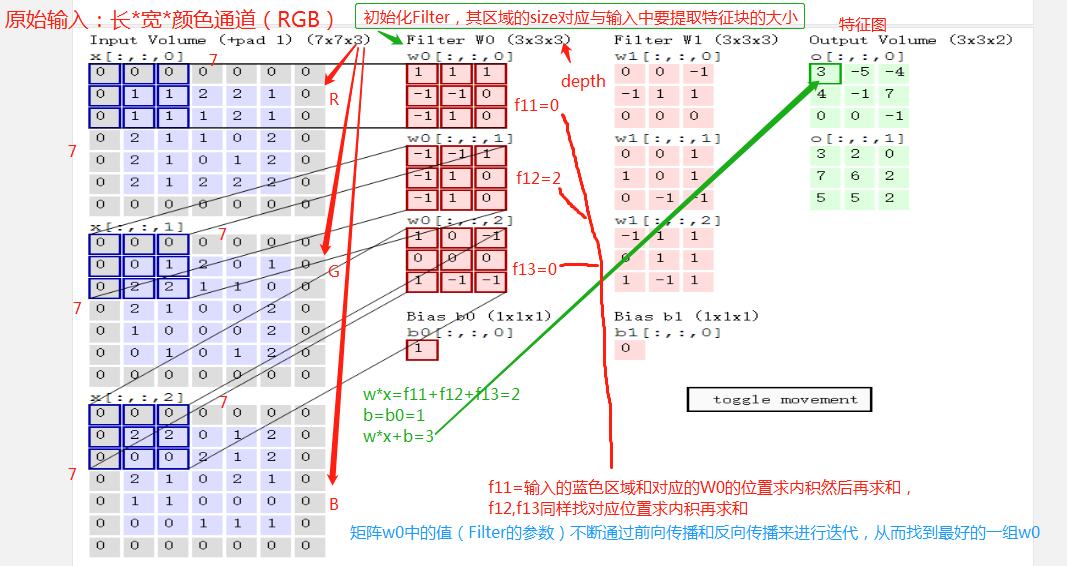
b的维度与特征图的数量（即每一层对的输出）相等。
输入图像和filter的对应位置元素相乘再求和，最后再加上b,得到特征图。如图中所示，filter w0的第一层深度和输入图像的蓝色方框中对应元素相乘再求和得到0，其他两个深度得到2，0，则有0+2+0+1=3即图中右边特征图的第一个元素3.，卷积过后输入图像的蓝色方框再滑动，stride=2，如下：
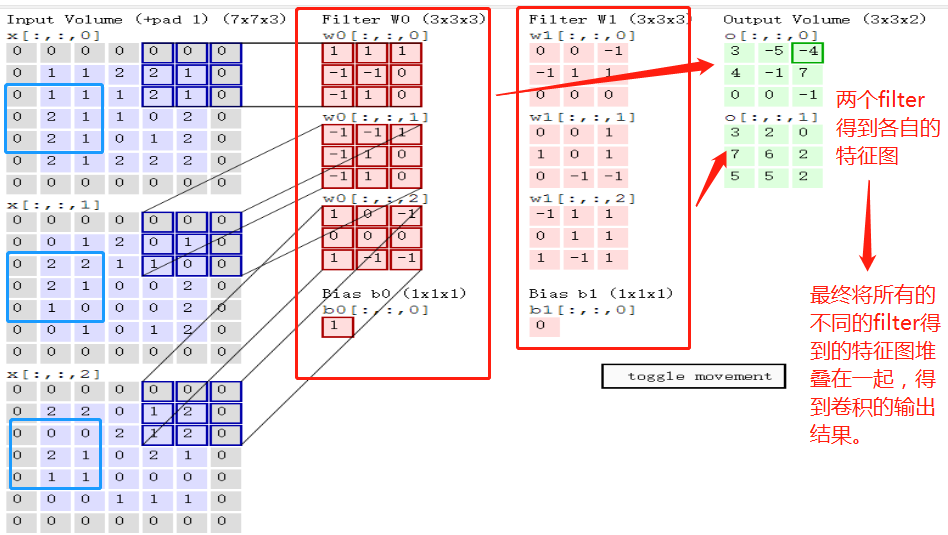
卷积核参数分析：
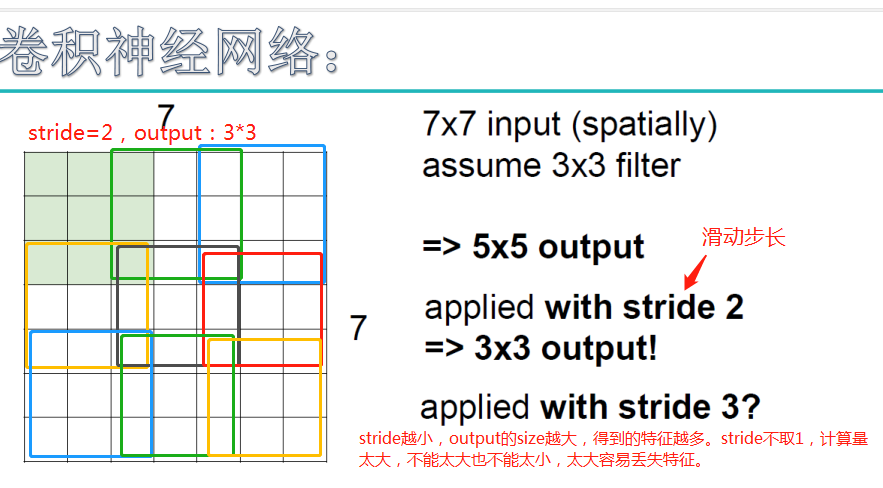
如上图，完成卷积，得到一个3*3*1的特征图；在这里还要注意一点，即zero pad项，即为图像加上一个边界，边界元素均为0.（对原输入无影响）一般有
F=3 => zero pad with 1
F=5 => zero pad with 2
F=7=> zero pad with 3,边界宽度是一个经验值，加上zero pad这一项是为了使输入图像和卷积后的特征图具有相同的维度，如：
输入为5*5*3，filter为3*3*3，在zero pad 为1，则加上zero pad后的输入图像为7*7*3，则卷积后的特征图大小为5*5*1（（7-3）/1+1），与输入图像一样；
关于特征图的大小计算方法具体如下：
例题：
Problem
输入图片大小为200×200，依次经过一层卷积（kernel size 5×5，padding 1，stride 2），pooling（kernel size 3×3，padding 0，stride 1），又一层卷积（kernel size 3×3，padding 1，stride 1）之后，输出特征图大小为：
答案：97
analysis
计算尺寸不被整除只在GoogLeNet中遇到过。卷积向下取整，池化向上取整。
（200-5+2*1）/2+1 为99.5，取99
（99-3）/1+1 为97
（97-3+2*1）/1+1 为97
答案是算出来了，我总感觉有点问题，后面的+1有点怪怪的
而我搜索的公式是下面这样的：
这里提供一个计算每一层输出图像的size的公式。无论是卷积层还是pooling层，公式都是这样的：
( input_size + 2*padding - kernel_size ) / stride = output_size
其中，padding指对input的图像边界补充一定数量的像素，目的是为了计算位于图像边界的像素点的卷积响应；kernel_size指卷积核的大小；stride指步长，即卷积核或者pooling窗口的滑动位移。另外需要注意，上面公式建立在所有参数都为整数的假设基础上。
卷及参数共享原则：
卷积层还有一个特性就是“权值共享”原则。
如没有这个卷积参数共享原则，则特征图由10个32*32*1的特征图组成，即每个特征图上有1024个神经元，每个神经元对应输入图像上一块5*5*3的区域，即一个神经元和输入图像的这块区域有75个连接，即75个权值参数，则共有75*1024*10=768000个权值参数，这是非常复杂的，因此卷积神经网络引入“权值”共享原则，即一个特征图上每个神经元对应的75个权值参数被每个神经元共享，这样则只需75*10=750个权值参数，而每个特征图的阈值（偏置项b）也共享，即需要10个阈值，则总共需要750+10=760个参数。
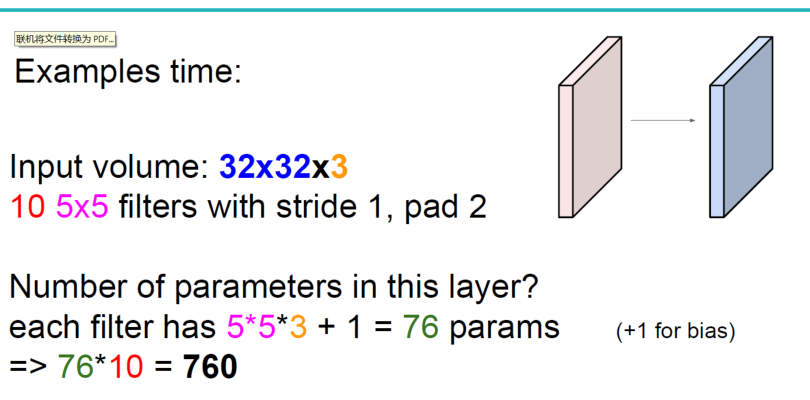
补充：权值共享时，只是在每一个filter上的每一个channel中是共享的；
权值共享指的是同层某些神经元之间的连接权值是共享的，局部感知指的是神经元之间的连接并非是全连接，是局部的。这两个特点能够极大减少连接权值的数量，降低模型复杂度。
全连接层缺点是参数很多，卷积层可以减少参数，减少计算量，因为卷积层的参数共享特性。
池化层（Pooling）原理：
池化层：对输入的特征图进行压缩，一方面使特征图变小，简化网络计算复杂度；一方面进行特征压缩，提取主要特征，如下：
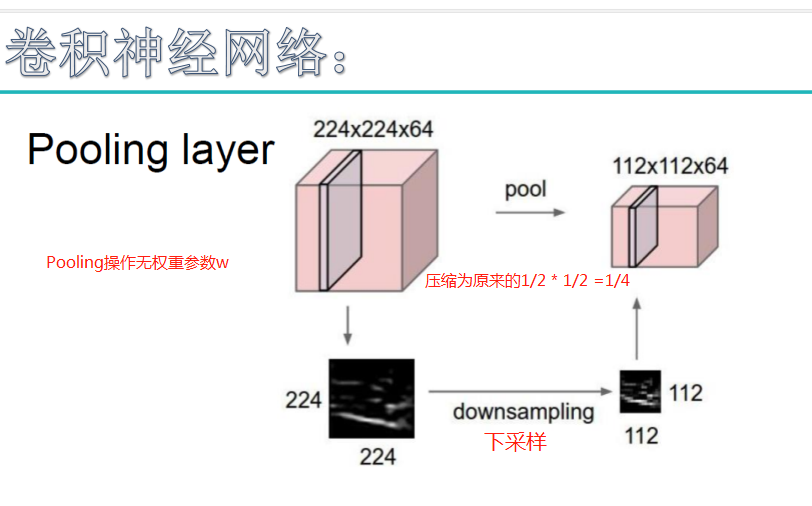
池化操作一般有两种，一种是Avy Pooling（或Mean Pooling）,一种是max Pooling,如下：
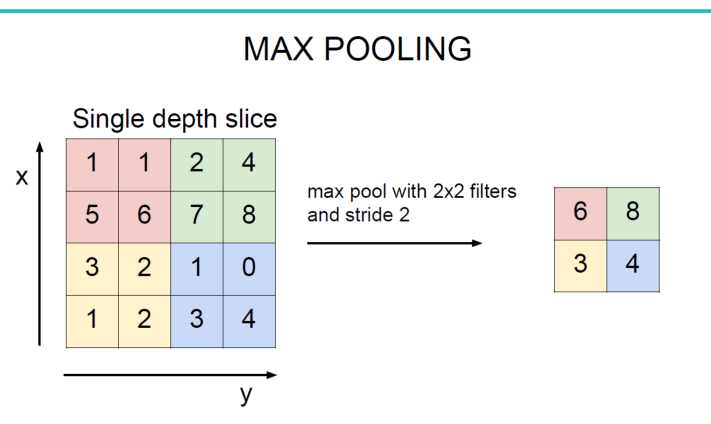
同样地采用一个2*2的filter,max pooling是在每一个区域中寻找最大值，这里的stride=2,最终在原特征图中提取主要特征得到右图。
（Avy pooling现在不怎么用了（其实就是平均池化层），方法是对每一个2*2的区域元素求和，再除以4，得到主要特征），而一般的filter取2*2,最大取3*3,stride取2，压缩为原来的1/4.
注意：这里的pooling操作是特征图缩小，有可能影响网络的准确度，因此可以通过增加特征图的深度来弥补（这里的深度变为原来的2倍）。
池化层
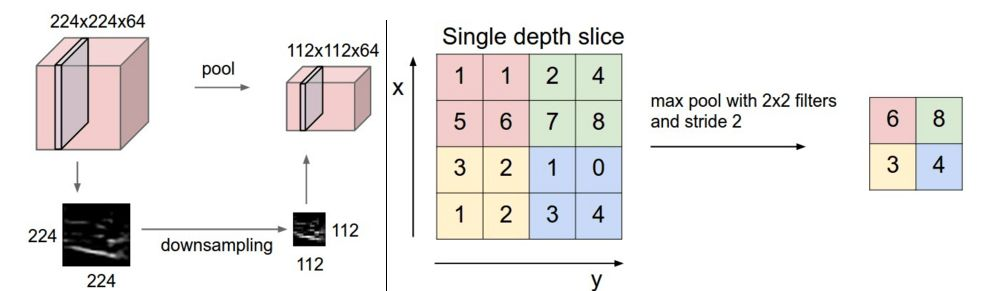
池化是一种非线性下采样的形式，让我们可以在保留最重要的特征的同时削减卷积输出。最常见的池化方法是最大池化，将输入图像（这里是卷积层的激活映射）分区（无重叠的矩形），然后每区取最大值。
池化的关键优势之一是降低参数数量和网络的计算量，从而缓解过拟合。此外，由于池化去除了特定特征的精确位置的信息，但保留了该特征相对其他特征的位置信息，结果也提供了平移不变性。
最常见的池化大小是2 x 2（步长2），也就是从输入映射中去除75%的激活。
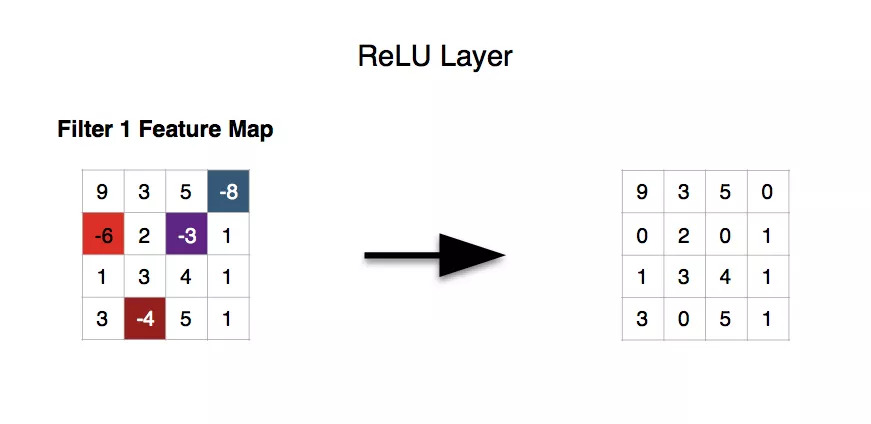
ReLU层
修正线性单元（Rectifier Linear Unit）层应用如下激活函数
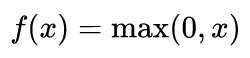
至池化层的输出。它在不影响卷积层的感受野的前提下增加了整个网络的非线性。当然，我们也可以应用其他标准的非线性激活函数，例如tanh和sigmoid。
全连接层：连接所有的特征，将输出值送给分类器（如softmax分类器）。
全连接层
获取ReLU层的输出，将其扁平化为单一向量，以便调节权重。
总的一个结构大致如下：
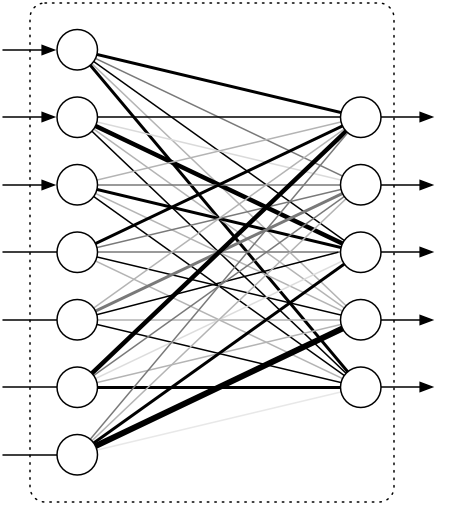
另外：CNN网络中前几层的卷积层参数量占比小，计算量占比大；而后面的全连接层正好相反，大部分CNN网络都具有这个特点。因此我们在进行计算加速优化时，重点放在卷积层；进行参数优化、权值裁剪时，重点放在全连接层。
每次都是这样：卷积+relu==》POOL==》卷积+relu==》POOL------==》全连接层FC+dropout==》全连接层FC+dropout==》（全连接层FC+softmax）用于分类。----》利用交叉熵损失函数进行更新。
在CNN中，dropout放在全连接层后加上，不在卷积层加。droupout不是去掉的比例，而是保存下的比例。
前两个全连接层用于特征提取，一般会指定2~3个全连接层，最后一层用于分类。
卷积神经网络反向传播原理：
注：上图中 ，对特征图不是分类，而是对特征图再卷积时要保证卷积和的层数，和前一层输入层数相同。
经典卷及网络架构实例：
1.经典神经网络有:2012年提出的AlexNet和2014年提出的VGGNet,结构图分别如下：
LeNet提出并成功地应用手写数字识别，但是很快，CNN的锋芒被SVM和手工设计的局部特征所掩盖。2012年，AlexNet在ImageNet图像分类任务竞赛中获得冠军，一鸣惊人，从此开创了深度神经网络空前的高潮。论文ImageNet Classification with Deep Convolutional Neural Networks （http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf）
AlexNet优势在于：
-
- 使用了非线性激活函数ReLU（如果不是很了解激活函数，可以参考我的另一篇博客 激活函数Activation Function（https://www.cnblogs.com/tianqizhi/p/9570975.html），并验证其效果在较深的网络超过Sigmoid，成功解决了Sigmoid在网络较深时的梯度弥散问题。
-
- 提出了LRN（Local Response Normalization），局部响应归一化，LRN一般用在激活和池化函数后，对局部神经元的活动创建竞争机制，使其中响应比较大对值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力
-
- 使用CUDA加速深度神经卷积网络的训练，利用GPU强大的并行计算能力，处理神经网络训练时大量的矩阵运算
-
- 在CNN中使用重叠的最大池化，AlexNet全部使用最大池化，避免平均池化的模糊化效果。AlexNet中提出让步长比池化核的尺寸小，这样池化层的输出之间会有重叠和覆盖，提升了特征的丰富性。
- 使用数据增广（data agumentation）和Dropout防止过拟合。【数据增广】随机地从256*256的原始图像中截取224*224大小的区域，相当于增加了2048倍的数据量；【Dropout】AlexNet在后面的三个全连接层中使用Dropout，随机忽略一部分神经元，以避免模型过拟合。
AlexNet总共包含8层，其中有5个卷积层和3个全连接层，有60M个参数，神经元个数为650k，分类数目为1000，LRN层出现在第一个和第二个卷积层后面，最大池化层出现在两个LRN层及最后一个卷积层后。
-
第一层输入图像规格为227*227*3，过滤器（卷积核）大小为11*11，深度为96，步长为4，则卷积后的输出为55*55*96，分成两组，进行池化运算处理，过滤器大小为3*3，步长为2，池化后的每组输出为27*27*48
-
第二层的输入为27*27*96，分成两组，为27*27*48，填充为2，过滤器大小为5*5，深度为128，步长为1，则每组卷积后的输出为27*27*128；然后进行池化运算，过滤器大小为3*3，步长为2，则池化后的每组输出为13*13*128
-
第三层两组中每组的输入为13*13*128，填充为1，过滤器尺寸为3*3，深度为192，步长为1，卷积后输出为13*13*192。在C3这里做了通道的合并，也就是一种串联操作，所以一个卷积核卷积的不再是单张显卡上的图像，而是两张显卡的图像串在一起之后的图像，所以卷积核的厚度为256，这也是为什么图上会画两个3*3*128的卷积核。
-
第四层两组中每组的输入为13*13*192，填充为1，过滤器尺寸为3*3，深度为192，步长为1，卷积后输出为13*13*192
-
第五层输入为上层的两组13*13*192，填充为1，过滤器大小为3*3，深度为128，步长为1，卷积后的输出为13*13*128；然后进行池化处理，过滤器大小为3*3，步长为2，则池化后的每组输出为6*6*128
-
第六层为全连接层，上一层总共的输出为6*6*256，所以这一层的输入为6*6*256，采用6*6*256尺寸的过滤器对输入数据进行卷积运算，每个过滤器对输入数据进行卷积运算生成一个结果，通过一个神经元输出，设置4096个过滤器，所以输出结果为4096
-
第六层的4096个数据与第七层的4096个神经元进行全连接
-
第八层的输入为4096，输出为1000（类别数目）
VGG模型是牛津大学VGG组提出的。论文为Very Deep Convolutional Networks for Large-Scale Image Recognition（https://arxiv.org/pdf/1409.1556） VGG全部使用了3*3的卷积核和2*2最大池化核通过不断加深网络结构来提神性能。采用堆积的小卷积核优于采用大的卷积核，因为多层非线性层可以增加网络深层来保证学习更复杂的模式，而且所需的参数还比较少。
-
- 两个堆叠的卷积层（卷积核为3*3）有限感受野是5*5，三个堆叠的卷积层（卷积核为3*3）的感受野为7*7，故可以堆叠含有小尺寸卷积核的卷积层来代替具有大尺寸的卷积核的卷积层，并且能够使得感受野大小不变，而且多个3*3的卷积核比一个大尺寸卷积核有更多的非线性（每个堆叠的卷积层中都包含激活函数），使得decision function更加具有判别性。
-
- 假设一个3层的3*3卷积层的输入和输出都有C channels，堆叠的卷积层的参数个数为
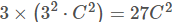，而等同的一个单层的7*7卷积层的参数为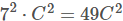
可以看到VGG-D使用了一种块结构：多次重复使用统一大小的卷积核来提取更复杂和更具有表达性的特征。VGG系列中，最多使用是VGG-16，下图来自Andrew Ng深度学习里面对VGG-16架构的描述。如图所示，在VGG-16的第三、四、五块：256、512、512个过滤器依次用来提取复杂的特征，其效果就等于一个带有3各卷积层的大型512*512大分类器。
传统的神经网络不一定层数（增加卷积层和池化层）越多越好，提取的特征可能会表少，并不一定能增加分类效果。
总结：VGG采用堆积的小卷积核替代采用大的卷积核，堆叠的小卷积核的卷积层等同于单个的大卷积核的卷积层，不仅能够增加决策函数的判别性还能减少参数量
可参考：【长文详解】卷积神经网络常见架构AlexNet、ZFNet、VGGNet、GoogleNet和ResNet模型的理论与实践
2.分类与回归：
（1）分类(classfication)：就是经过经过一系列的卷积层和池化层之后，再经过全连接层得到样本属于每个类的得分，再用比如softmax分类其对其进行分类；
（2）回归（regression）:相当于用一个矩形框来框住要识别的物体,即localization;
如下：
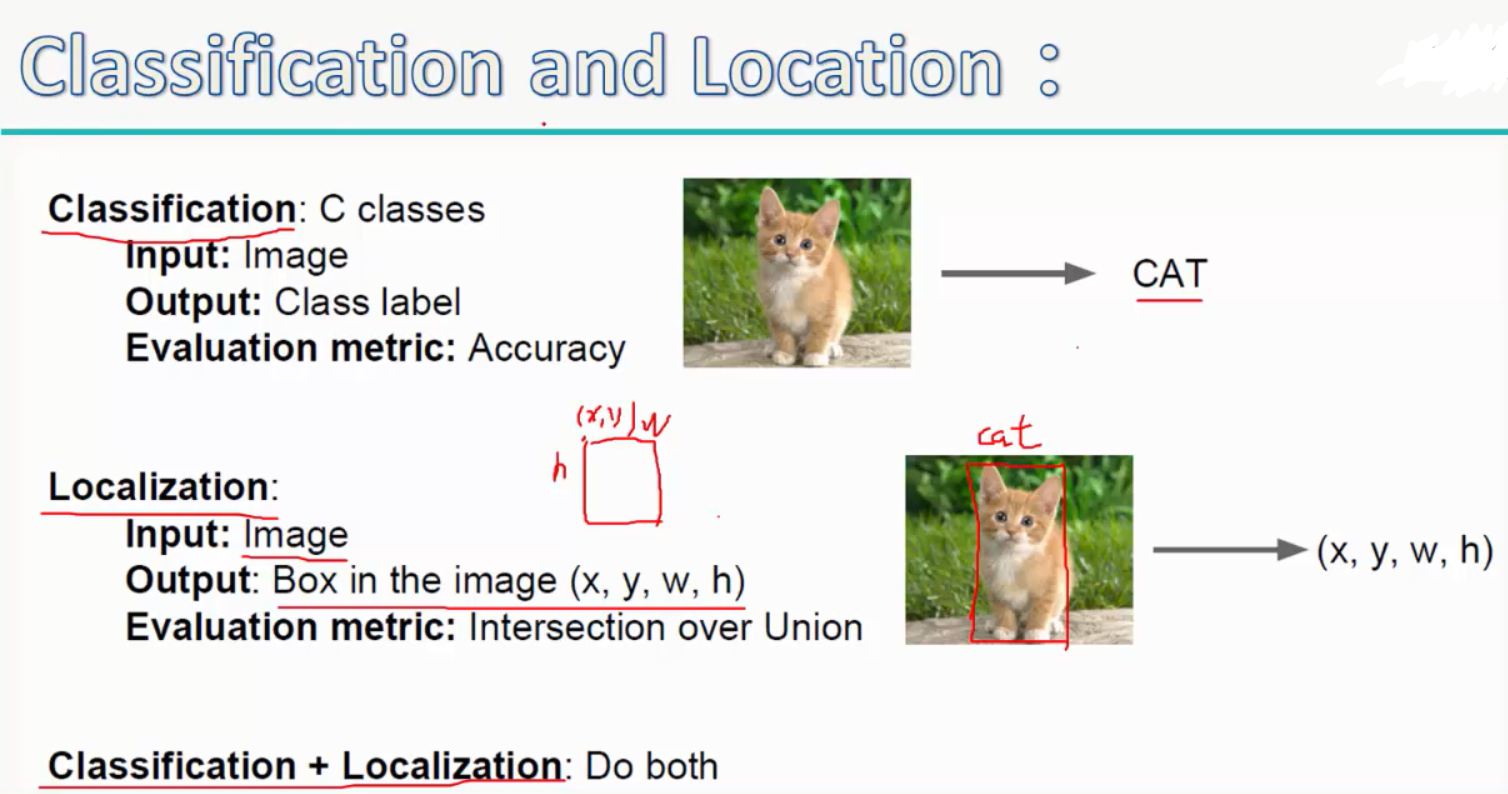
这里，回归用了拟合的方法，即给定输入中物体的位置(x,yw,h)，再用卷积网络的输出(x',y',w',h')去拟合正确的位置，Loss值是两者之间的欧式距离：
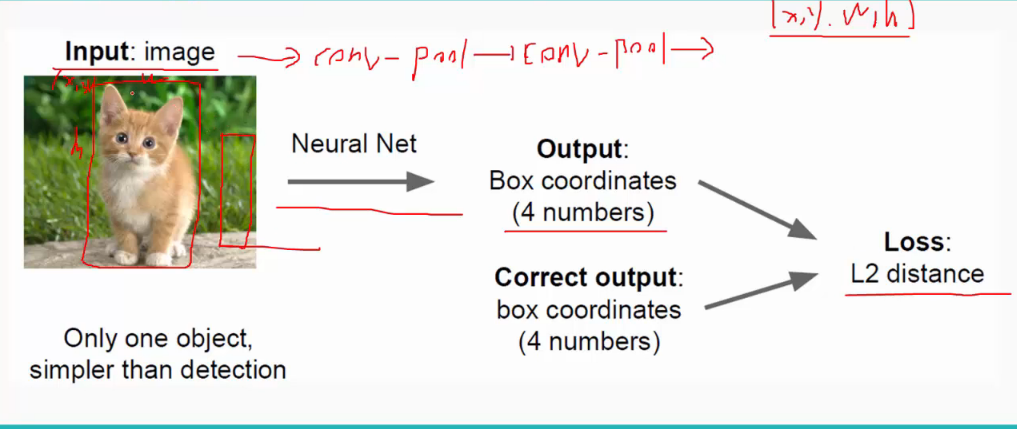
所以最终经过全连接层要做两件事，即classfication和localization：
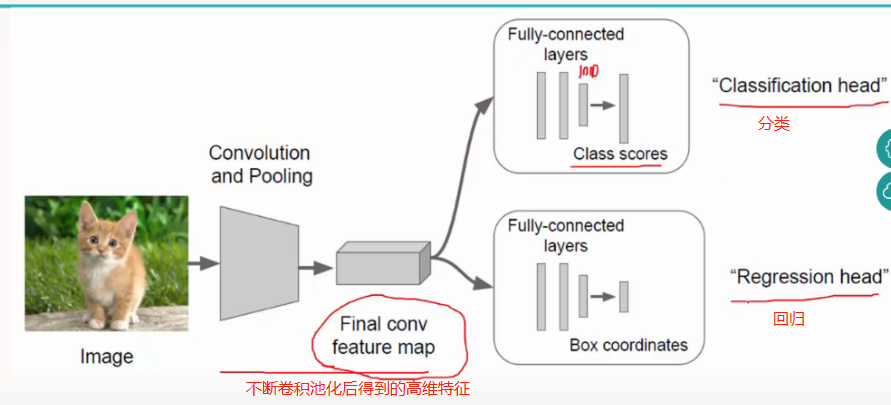
好的，下面再说一下CNN卷积神经网络的的训练过程：
（1）选定模型（经典模型有VGGNet、AlexNet、GoogleNet；VGG最常用）：
这里不需要自己从零开始初始化权值和阈值等参数，采用fine tune，即利用别人训练好的模型来训练自己的网络，用别人的参数，自己再进行微调。（有时候别人的实现功能可能与我们不太一样，比如别人需要分1000类，而我们只需分10类，这时候只需修改全连接层即可，前面的不需修改）
（2）添加回归模块；
（3）训练网络；
（4）测试；
过程如下：
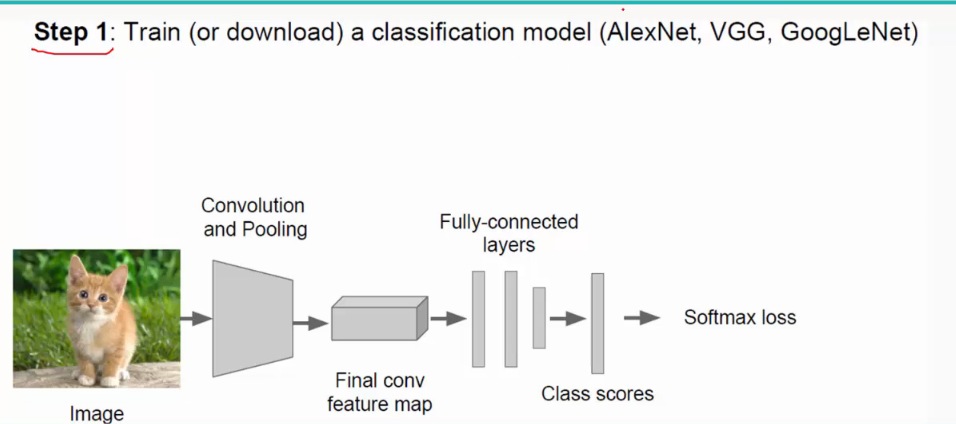
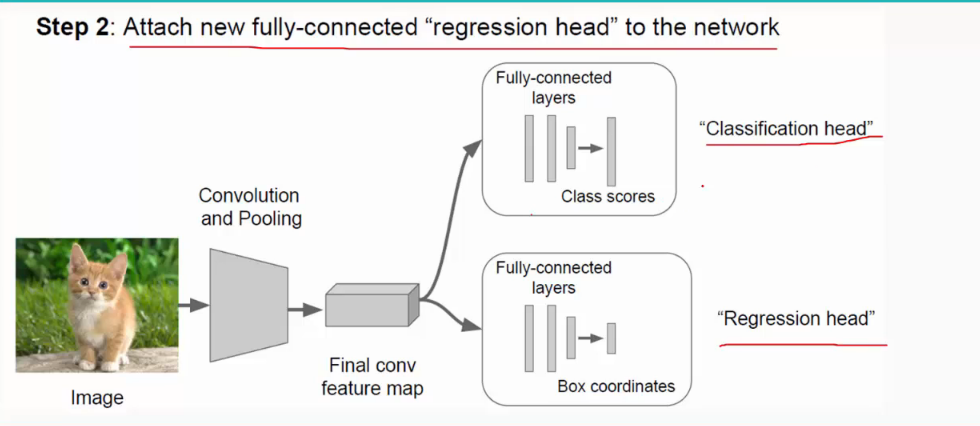
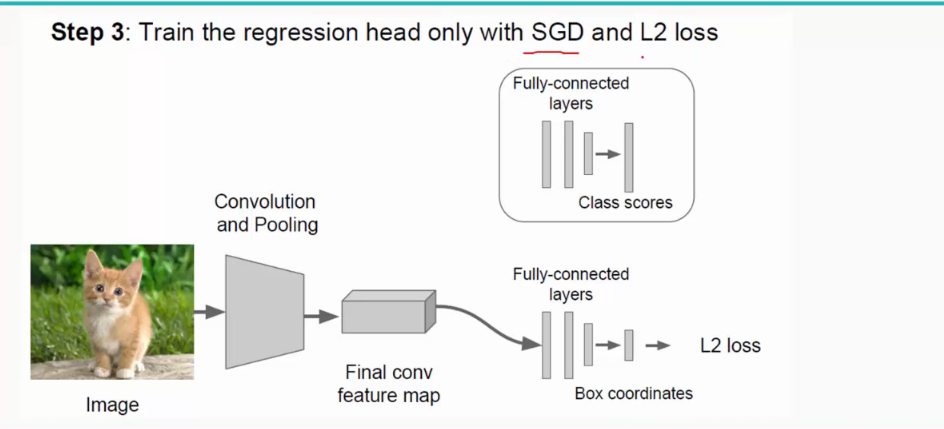注：SGD：随机梯度下降
注：回归具体加在哪里？要具体试以下，然后对比下准确度，再决定加在哪里
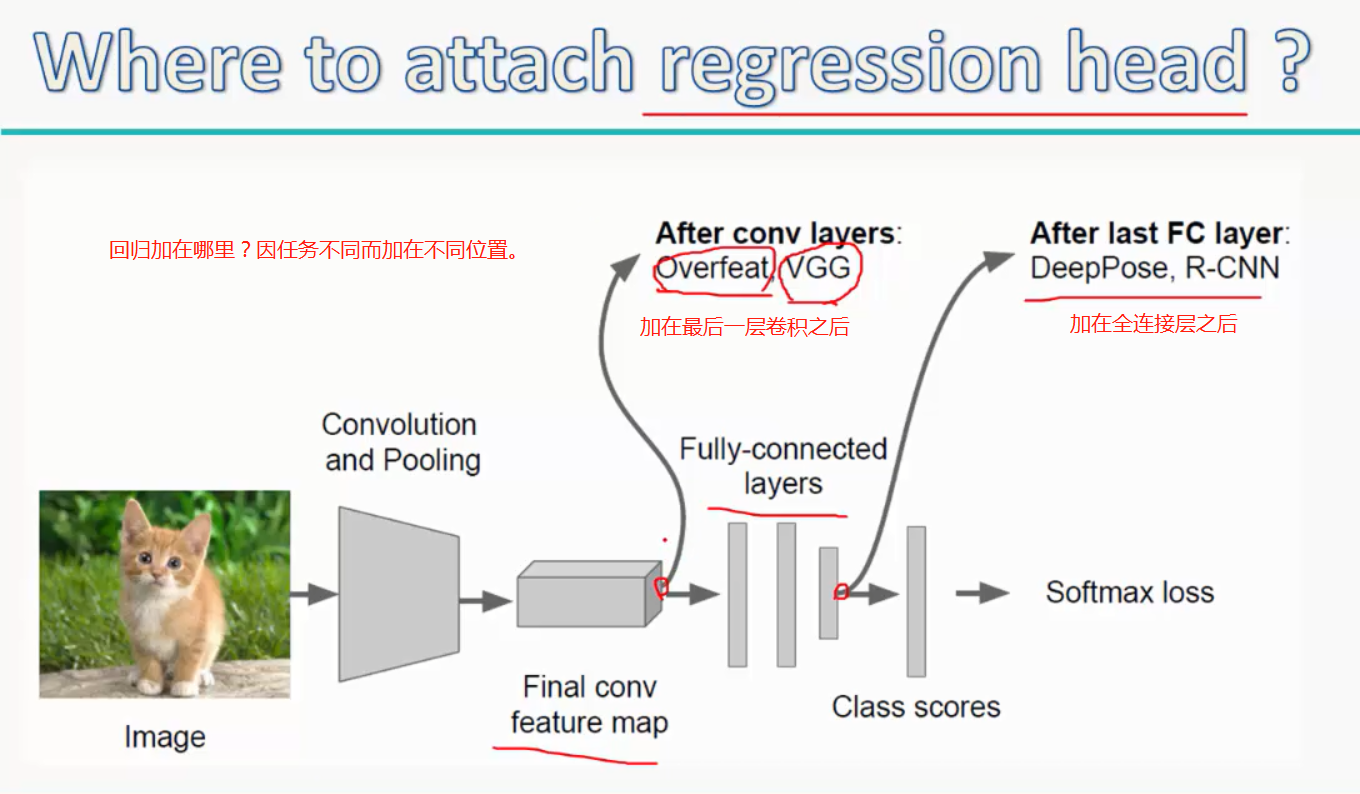
而regression head（回归模块）的位置一般放在最后一层卷积层之后（对于overfeat、VGG）或者全连接层之后（对于DeepPose、R-CNN）。
当然用这种回归的方法，我们还可以做其他的事，比如pose estimation(人体姿势辨别),就是定位出物体上的n个点并连线，可由形状判断物体的行为：
第一步：找到关键点，比如膝盖坐标（x1,y1），肩膀坐标（x2,y2），等等。回归的任务时预测这些坐标（这些坐标都是有label的，比如x1,y1为膝盖），然后去拟合这些点，计算l2 距离（欧式距离），使得这些点不断朝着正确的方向前进，最终直到训练数据的点能完全拟合给定正确姿势位置的点，这样就完成了回归的任务。这里是人体关键点，更常见的是人脸关键点。
再寻找location的过程中，最常用的是Sliding Window(滑动窗口，属于分类任务)：即对于一个输入，用一个比如说3*3的固定大小的滑动窗口在图像中不断移动，每移动到一个区域，可以用训练好的网络如VGGNet来算出属于"猫"的概率，直至滑完所有的区域，看概率最高的是哪一块区域，那块区域即为最终的location：
这里还要注意一点，在使用sliding window时还要对输入图像进行预处理，scale变换，即将原输入图像放大放小为一系列大小不同的图像，再用固定大小的sliding window去滑动，这样做是为了检测物体在不同图像中大小不同时的位置。
当然这么做是很费力的，因为滑动窗口一般较小，对于每一个输入可能都需要滑动很多次，而每滑动一次就要遍历一次CNN，这是非常占内存的，因此还有一种更加简便的方法，叫做Region Proposals(区域建议)：将输入图像中有用的物体都框出来作为候选框，再用selective search算法，即对于这n个候选框，将图像的像素特性或者纹理特性类似或有相同规律的框合并成大的框，一般这样最终的框就是Location:
注：物体检测
做分类的话需要用滑动窗口不断去滑，所产生的问题是：
按上述分类做的话耗时耗力，又太笨，聪明的做法：
候选框的制作有多种算法，selective search是最常规的算法：
如何寻找有效的候选框，最开始的就是这个方法。
寻找方法就是一开始把一幅图像，分割成无数个候选框构造而成的（convert regions to boxes）
然后根据一些色彩特征、把候选框进行融合，框数量变小了，框变大；效果就是逐渐、慢慢找到最好的框
参考：https://blog.csdn.net/mydear_11000/article/details/71775018
下面再介绍一下R-CNN以及它的训练过程，和CNN类似，不过最后一步是将feature先固话到disk上，再进行回归：
图像中的候选框，每个boxes跑一次卷积神经网络（一张图大概2000个框）。conv之后接SVM/reg，进行判断，论文中用SVM来进行分类（比softmax好一些）
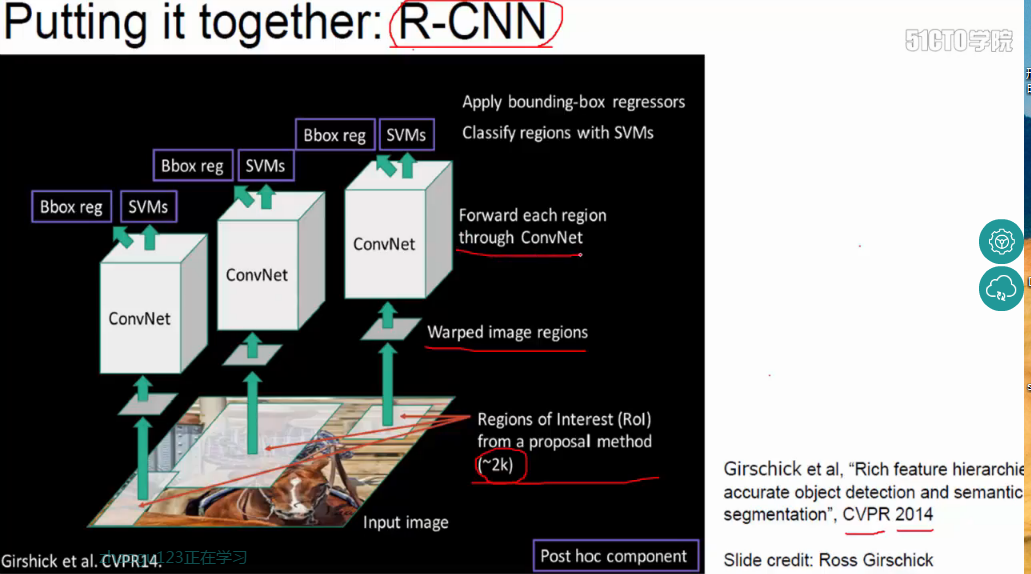注：Warped image regions操作是为了将提取到的大小不一的候选框统一为大小相同的框。
但是，每个都要计算太浪费时间了，最开始，需要把数据固化到硬盘很占容量，同时分类用SVM也非常耗时，效率不高。
具体步骤：
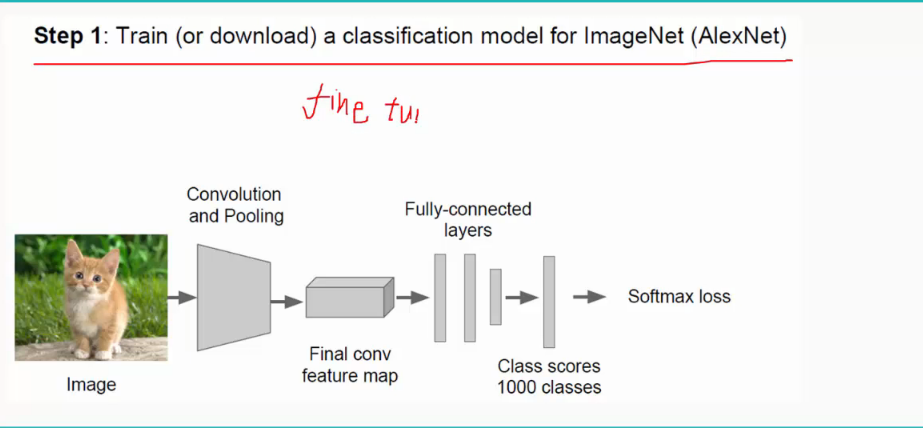
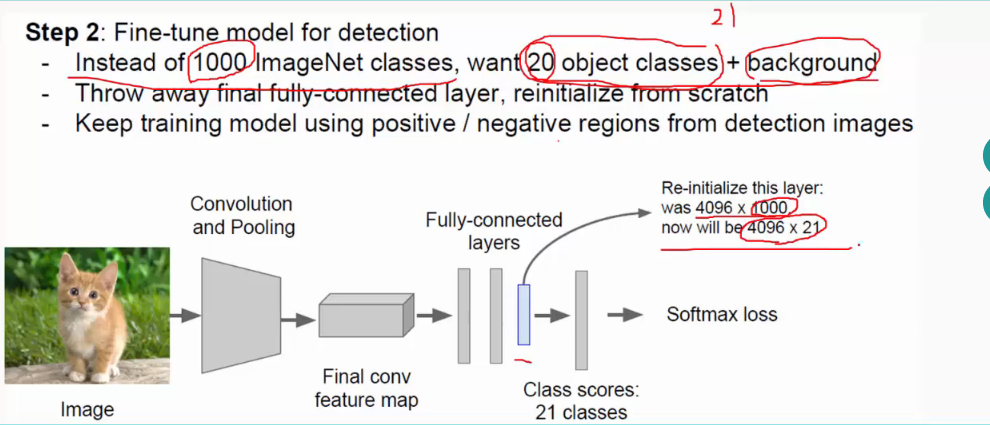
由上可知：R-CNN有两个缺点：（1）对于每一个region proposal都有进行一次CNN，所以测试时间非常慢;
(2)过程繁琐，先进行固化再进行提取等。
而后有fast R-CNN:使用卷积共享，对所有的region只进行一次CNN;不需固化：
注：R-CNN没有做卷积共享。
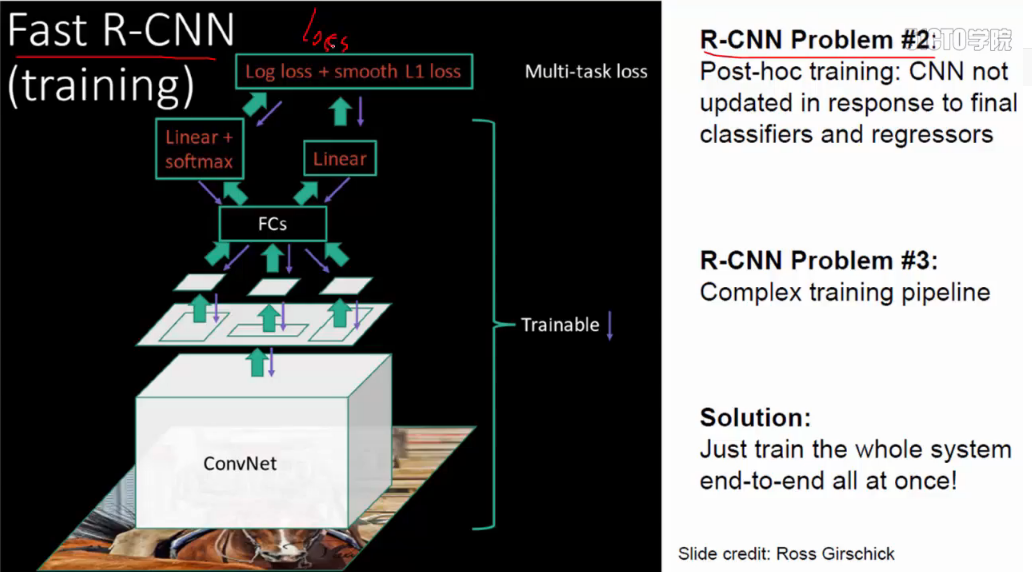
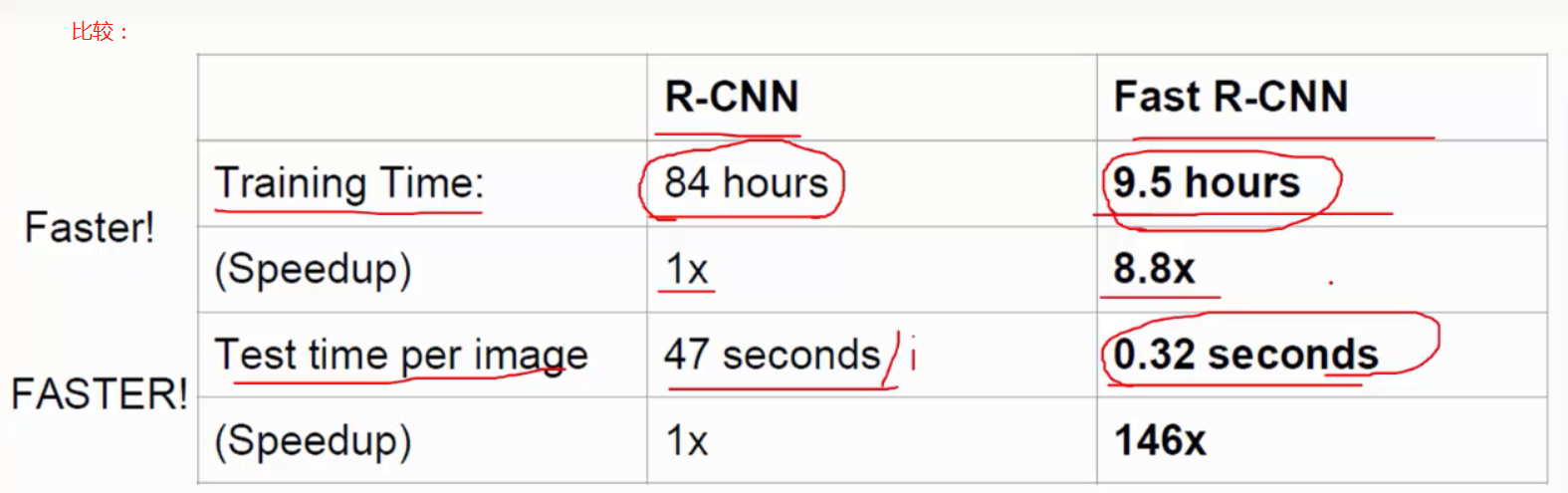
在RCNN中CNN阶段的流程大致如下：
红色框是selective search 输出的可能包含物体的候选框（ROI）。
一张图图片会有~2k个候选框，每一个都要单独输入CNN做卷积等操作很费时，从比较图结果中就可以看出，Test time per image with Selective search远远大于Test time per image
faster R-CNN：将selective search整合到Net中，即在网络中添加一层region proposal network(RPN),不需要在原输入图像中找候选框，而是在卷积之后的特征图中找框，提高了速度：
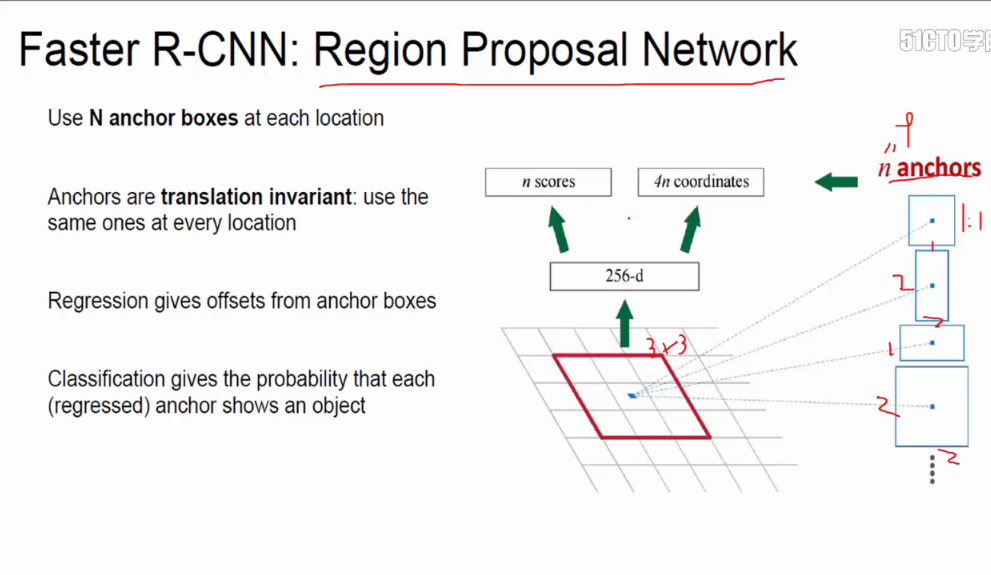
**RPN可以很有效地共享卷积成果。**RCNN是基于像素点来做的，先提取框，后卷积，有几个框就要多少次卷积；RPN是卷积之上的特征图来的，先卷积，共享卷积成果（效率更高的切入点），只需要一次卷积。
- （1）RPN候选框生成阶段。
在VGG中的最后一层卷积层的特征图中，找到某一个点，通过感受野，还原到原始图像，变成了9张大小不同的框anchor boxes，像素（128,256,521）*比率（1:1，1:2，1:3）1个点，模拟出9个候选框。其中弱候选框有超出边界的话，则去掉。
- （2）分类阶段。
选出候选框之后，接上分类对候选框进行判断。
- （3）微调阶段。
选定一些框之后，需要对框框进行最后的微调box regression、box回归。计算差异（长宽比），然后作了微调，box regression 
- （4）ROI pooling层阶段
spatial pyramid pooling（SPP layer）为最后输出做准备。做了微调之后，候选框大小不一样，通过调整pooling的滑块，调整到相同的结果。
- 问题一：真的要画这9个候选框吗？
答：不是。卷积层每个点演化成9个框，而9个框则是虚构出来的，而没有真正画在图像上。
- 问题二：感受野
计算感受野的时候，在计算未来的候选框大小，VGG网络只需要根据pooling层来计算即可，因为卷积层不会矿大、缩小感受野。
- 问题三：分类任务实质上并不是二分类
之后再接分类softmax层判断候选框是否有物体。但是根据源码来看，并不是二分类（是否有物体），而是18分类。通过定义loss function来实现成9个框，9个框计算正负的概率，那就是18个结果。
- 问题四：如何判断候选框是有物体的？
根据给定的训练集的输入数据的四个坐标（x,y,m,h）的groud truth，看重合部分，大于0.7，认为是一个物体（正例，前景），小于0.3认为不是一个物体（负例，背景）
将R-CNN、fast R-CNN、faster R-CNN进行对比如下：
循环神经网络RNN网络结构：
https://www.jianshu.com/p/9dc9f41f0b29
https://blog.csdn.net/heyongluoyao8/article/details/48636251
什么是RNNs（通俗易懂版解释）
人类并不是每时每刻都从一片空白的大脑开始他们的思考。在你阅读这篇文章时候，你都是基于自己已经拥有的对先前所见词的理解来推断当前词的真实含义。我们不会将所有的东西都全部丢弃，然后用空白的大脑进行思考。我们的思想拥有持久性。
传统的神经网络并不能做到这点，看起来也像是一种巨大的弊端。例如，假设你希望对电影中的每个时间点的时间类型进行分类。传统的神经网络应该很难来处理这个问题——使用电影中先前的事件推断后续的事件。
RNN 解决了这个问题。RNN 是包含循环的网络，允许信息的持久化。
在上面的示例图中，神经网络的模块，A，正在读取某个输入 x_i，并输出一个值 h_i。循环可以使得信息可以从当前步传递到下一步。
这些循环使得 RNN 看起来非常神秘。然而，如果你仔细想想，这样也不比一个正常的神经网络难于理解。RNN 可以被看做是同一神经网络的多次复制，每个神经网络模块会把消息传递给下一个。所以，如果我们将这个循环展开：
什么是RNNs（理论性解释）
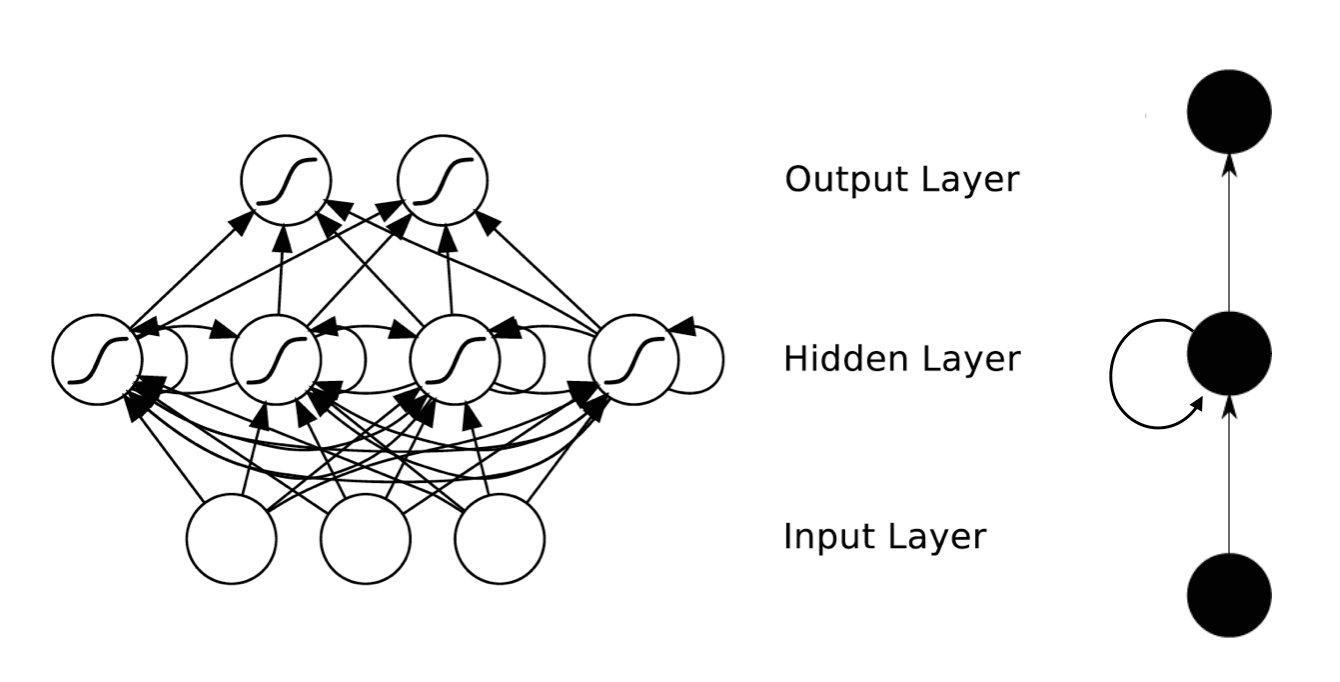
RNNs的目的使用来处理序列数据。在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种普通的神经网络对于很多问题却无能无力。例如，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。RNNs之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。理论上，RNNs能够对任何长度的序列数据进行处理。但是在实践中，为了降低复杂性往往假设当前的状态只与前面的几个状态相关，下图便是一个典型的RNNs：
长期依赖（Long-Term Dependencies）问题
RNN 的关键点之一就是他们可以用来连接先前的信息到当前的任务上，例如使用过去的视频段来推测对当前段的理解。如果 RNN 可以做到这个，他们就变得非常有用。但是真的可以么？答案是，还有很多依赖因素。有时候，我们仅仅需要知道先前的信息来执行当前的任务。例如，我们有一个 语言模型用来基于先前的词来预测下一个词。如果我们试着预测 “the clouds are in the sky” 最后的词，我们并不需要任何其他的上下文 —— 因此下一个词很显然就应该是 sky。在这样的场景中，相关的信息和预测的词位置之间的间隔是非常小的，RNN 可以学会使用先前的信息。
不太长的相关信息和位置间隔
但是同样会有一些更加复杂的场景。假设我们试着去预测“I grew up in France... I speak fluent French”最后的词。当前的信息建议下一个词可能是一种语言的名字，但是如果我们需要弄清楚是什么语言，我们是需要先前提到的离当前位置很远的 France 的上下文的。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。不幸的是，在这个间隔不断增大时，RNN 会丧失学习到连接如此远的信息的能力。也就是说相关信息和当前预测位置之间的间隔增大会造成两方面的问题，第一梯度消失，第二计算量特别大。
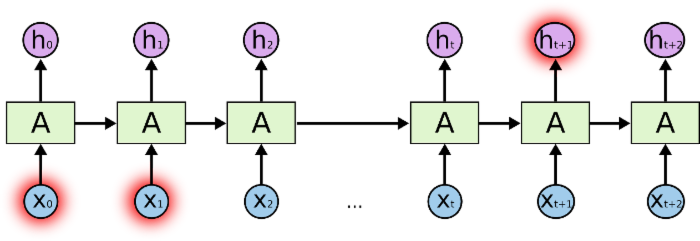
相当长的相关信息和位置间隔
在理论上，RNN 绝对可以处理这样的 长期依赖 问题。人们可以仔细挑选参数来解决这类问题中的最初级形式，但在实践中，RNN 肯定不能够成功学习到这些知识。 Bengio, et al. (1994) 等人对该问题进行了深入的研究，他们发现一些使训练 RNN 变得非常困难的相当根本的原因。
然而，幸运的是，LSTM 并没有这个问题！
LSTM 网络(长短记忆网络)
Long Short Term 网络—— 一般就叫做 LSTM ——是一种 RNN 特殊的类型，可以学习长期依赖信息。LSTM 由Hochreiter & Schmidhuber (1997)提出，并在近期被Alex Graves进行了改良和推广。在很多问题，LSTM 都取得相当巨大的成功，并得到了广泛的使用。
LSTM 通过刻意的设计来避免长期依赖问题。记住长期的信息在实践中是 LSTM 的默认行为，而非需要付出很大代价才能获得的能力！
所有 RNN 都具有一种重复神经网络模块的链式的形式。在标准的 RNN 中，这个重复的模块只有一个非常简单的结构，例如一个 tanh 层（激活函数）。
LSTM 同样是这样的结构，但是重复的模块拥有一个不同的结构。不同于 单一神经网络层，这里是有四个，以一种非常特殊的方式进行交互。
不必担心这里的细节。我们会一步一步地剖析 LSTM 解析图。现在，我们先来熟悉一下图中使用的各种元素的图标。
在上面的图例中，每一条黑线传输着一整个向量，从一个节点的输出到其他节点的输入。粉色的圈代表 pointwise 的操作，诸如向量的和，而黄色的矩阵就是学习到的神经网络层。合在一起的线表示向量的连接，分开的线表示内容被复制，然后分发到不同的位置。
LSTM 的核心思想
LSTM 的关键就是细胞状态，水平线在图上方贯穿运行。
细胞状态类似于传送带。直接在整个链上运行，只有一些少量的线性交互。信息在上面流传保持不变会很容易。
LSTM 有通过精心设计的称作为“门”的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个 sigmoid 神经网络层和一个 pointwise 乘法操作。
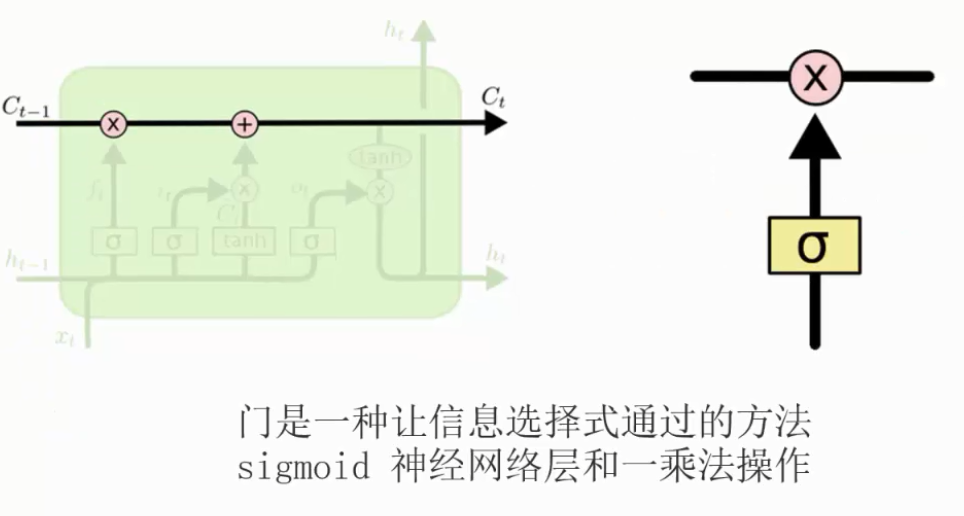
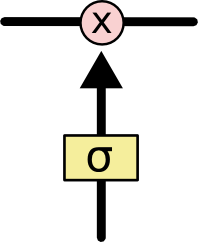
Sigmoid 层输出 0 到 1 之间的数值，描述每个部分有多少量可以通过。0 代表“不许任何量通过”，1 就指“允许任意量通过”！
LSTM 拥有三个门，来保护和控制细胞状态。
逐步理解 LSTM
在我们 LSTM 中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为忘记门层完成。该门会读取 h_{t-1} 和 x_t，输出一个在 0 到 1 之间的数值给每个在细胞状态 C_{t-1} 中的数字。1 表示“完全保留”，0 表示“完全舍弃”。
让我们回到语言模型的例子中来基于已经看到的预测下一个词。在这个问题中，细胞状态可能包含当前主语的性别，因此正确的代词可以被选择出来。当我们看到新的主语，我们希望忘记旧的主语。
\tilde{C}_t，会被加入到状态中。下一步，我们会讲这两个信息来产生对状态的更新。
在我们语言模型的例子中，我们希望增加新的主语的性别到细胞状态中，来替代旧的需要忘记的主语。
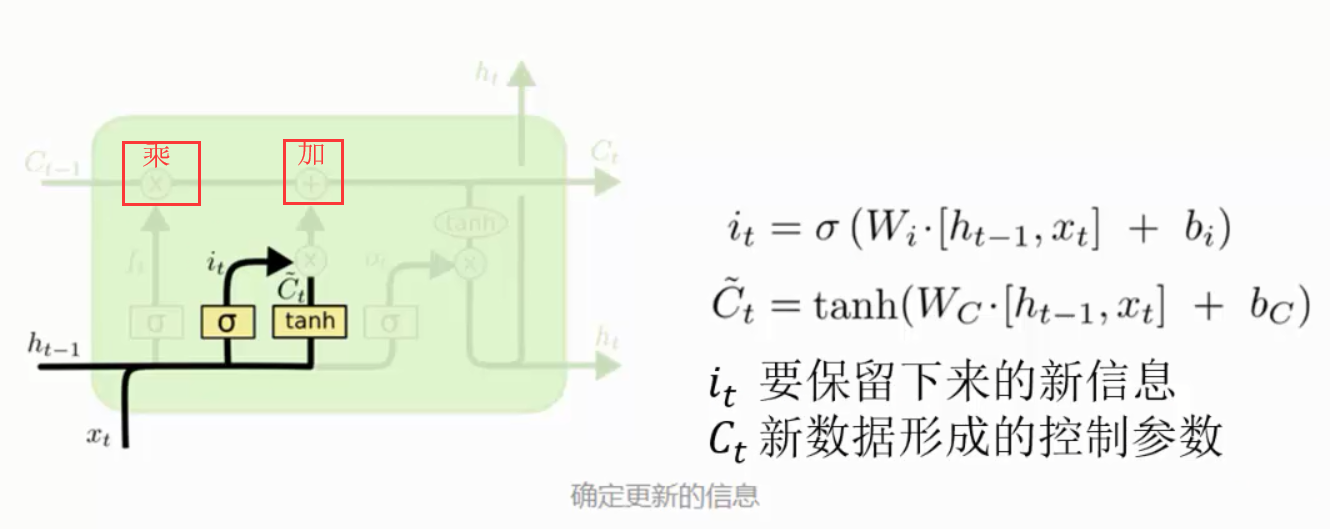
现在是更新旧细胞状态的时间了，C_{t-1} 更新为 C_t。前面的步骤已经决定了将会做什么，我们现在就是实际去完成。
我们把旧状态与 f_t 相乘，丢弃掉我们确定需要丢弃的信息。接着加上 i_t * \tilde{C}_t。这就是新的候选值，根据我们决定更新每个状态的程度进行变化。
在语言模型的例子中，这就是我们实际根据前面确定的目标，丢弃旧代词的性别信息并添加新的信息的地方。
最终，我们需要确定输出什么值。这个输出将会基于我们的细胞状态，但是也是一个过滤后的版本。首先，我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。接着，我们把细胞状态通过 tanh 进行处理（得到一个在 -1 到 1 之间的值）并将它和 sigmoid 门的输出相乘，最终我们仅仅会输出我们确定输出的那部分。
在语言模型的例子中，因为他就看到了一个 代词，可能需要输出与一个 动词 相关的信息。例如，可能输出是否代词是单数还是负数，这样如果是动词的话，我们也知道动词需要进行的词形变化。
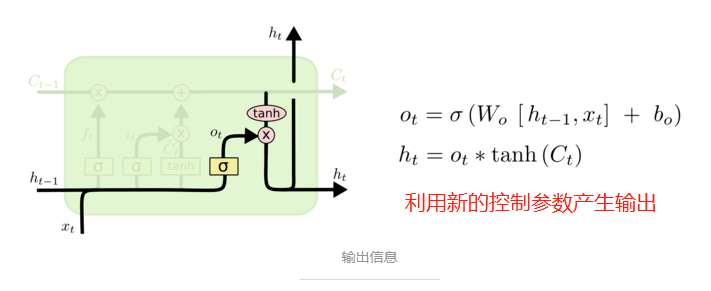
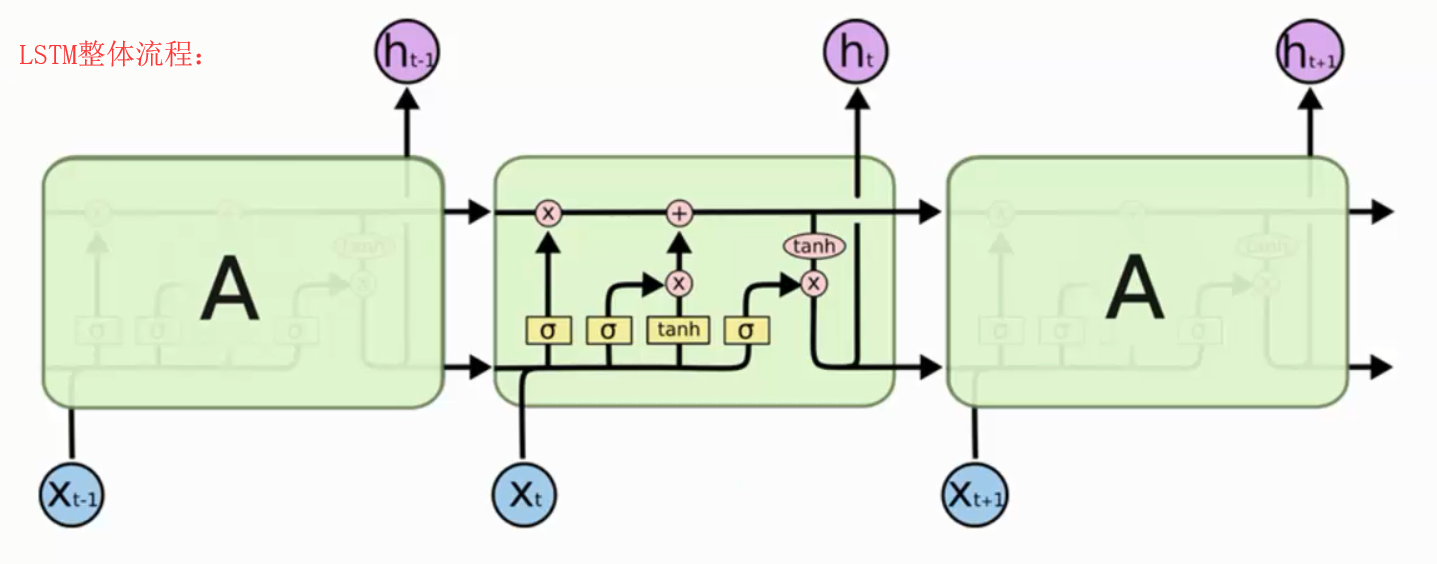
实际应用中LSTM比RNN应用更广，解决了RNN的长期依赖产生的问题。
LSTM 的变体
我们到目前为止都还在介绍正常的 LSTM。但是不是所有的 LSTM 都长成一个样子的。实际上，几乎所有包含 LSTM 的论文都采用了微小的变体。差异非常小，但是也值得拿出来讲一下。
其中一个流形的 LSTM 变体，就是由 Gers & Schmidhuber (2000) 提出的，增加了 “peephole connection”。是说，我们让 门层 也会接受细胞状态的输入。
上面的图例中，我们增加了 peephole 到每个门上，但是许多论文会加入部分的 peephole 而非所有都加。
另一个变体是通过使用 coupled 忘记和输入门。不同于之前是分开确定什么忘记和需要添加什么新的信息，这里是一同做出决定。我们仅仅会当我们将要输入在当前位置时忘记。我们仅仅输入新的值到那些我们已经忘记旧的信息的那些状态 。
要问哪个变体是最好的？其中的差异性真的重要吗？Greff, et al. (2015) 给出了流行变体的比较，结论是他们基本上是一样的。Jozefowicz, et al. (2015) 则在超过 1 万种 RNN 架构上进行了测试，发现一些架构在某些任务上也取得了比 LSTM 更好的结果。
结论
刚开始，我提到通过 RNN 得到重要的结果。本质上所有这些都可以使用 LSTM 完成。对于大多数任务确实展示了更好的性能！
由于 LSTM 一般是通过一系列的方程表示的，使得 LSTM 有一点令人费解。然而本文中一步一步地解释让这种困惑消除了不少。
LSTM 是我们在 RNN 中获得的重要成功。很自然地，我们也会考虑：哪里会有更加重大的突破呢？在研究人员间普遍的观点是：“Yes! 下一步已经有了——那就是注意力！” 这个想法是让 RNN 的每一步都从更加大的信息集中挑选信息。例如，如果你使用 RNN 来产生一个图片的描述，可能会选择图片的一个部分，根据这部分信息来产生输出的词。实际上，Xu, et al.(2015)已经这么做了——如果你希望深入探索注意力可能这就是一个有趣的起点！还有一些使用注意力的相当振奋人心的研究成果，看起来有更多的东西亟待探索……
注意力也不是 RNN 研究领域中唯一的发展方向。例如，Kalchbrenner, et al. (2015) 提出的 Grid LSTM 看起来也是很有前途。使用生成模型的 RNN，诸如Gregor, et al. (2015) Chung, et al. (2015) 和 Bayer & Osendorfer (2015) 提出的模型同样很有趣。在过去几年中，RNN 的研究已经相当的燃，而研究成果当然也会更加丰富！
