聚类算法_案例实战：聚类实战

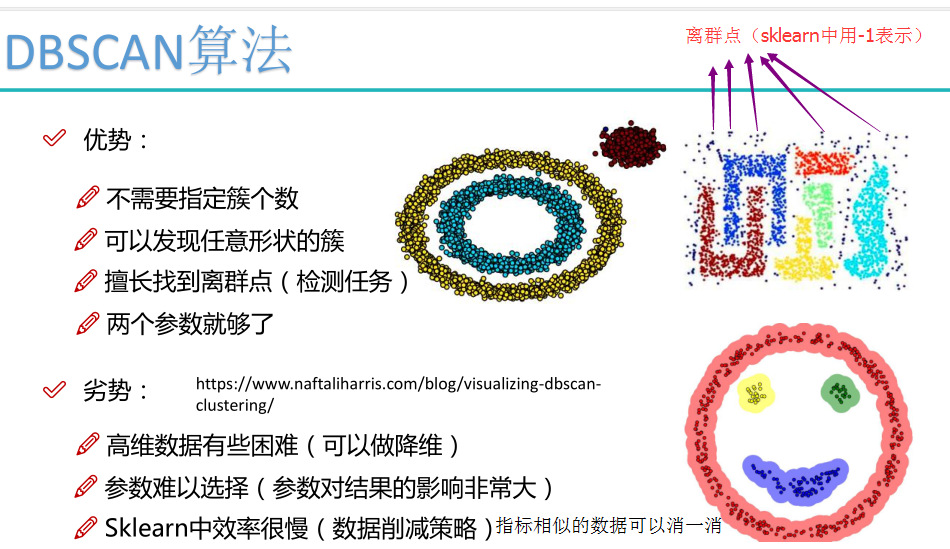
K-MEANS算法

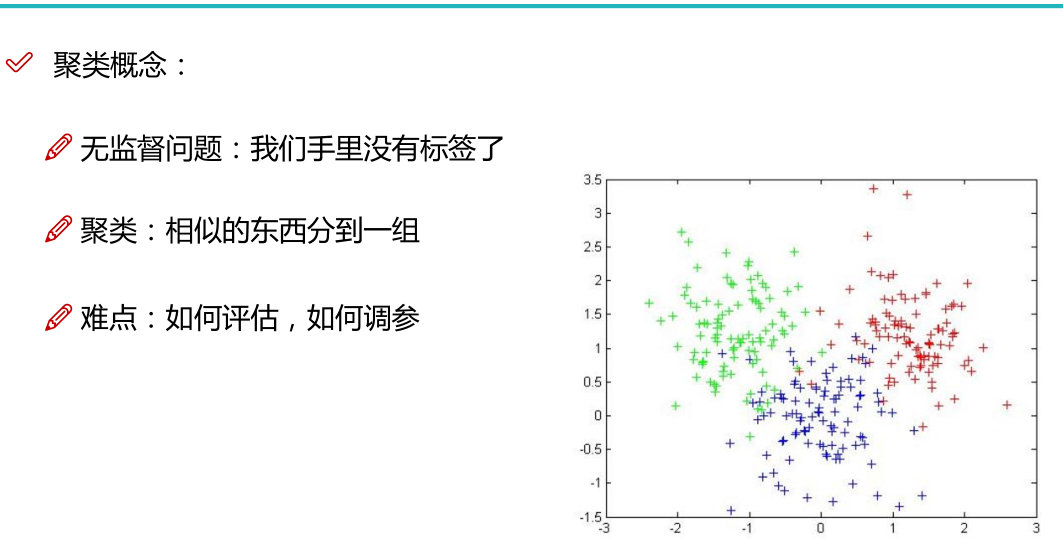
标准化：将数据的值按比例值缩放，归一化到0~1范围内，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

 

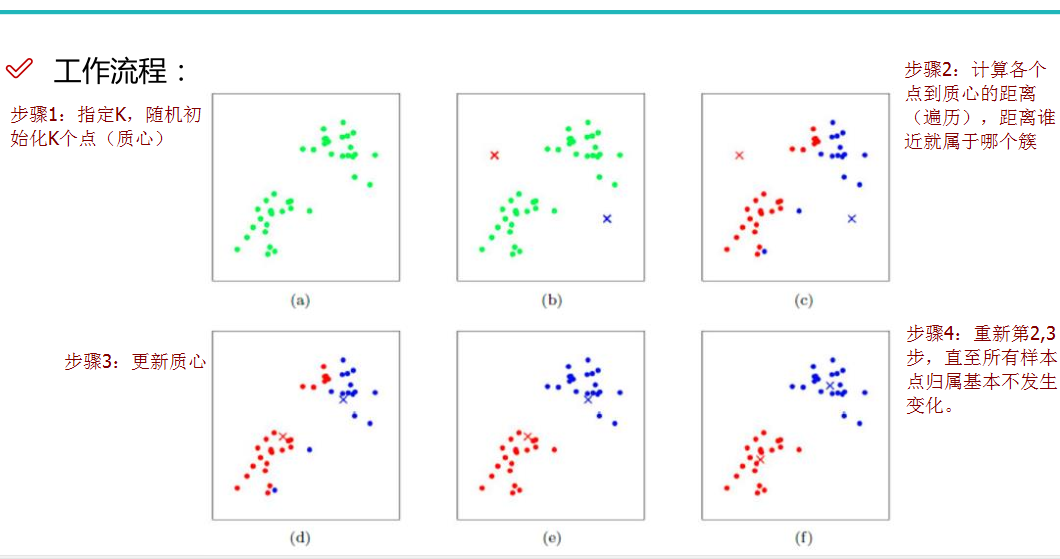
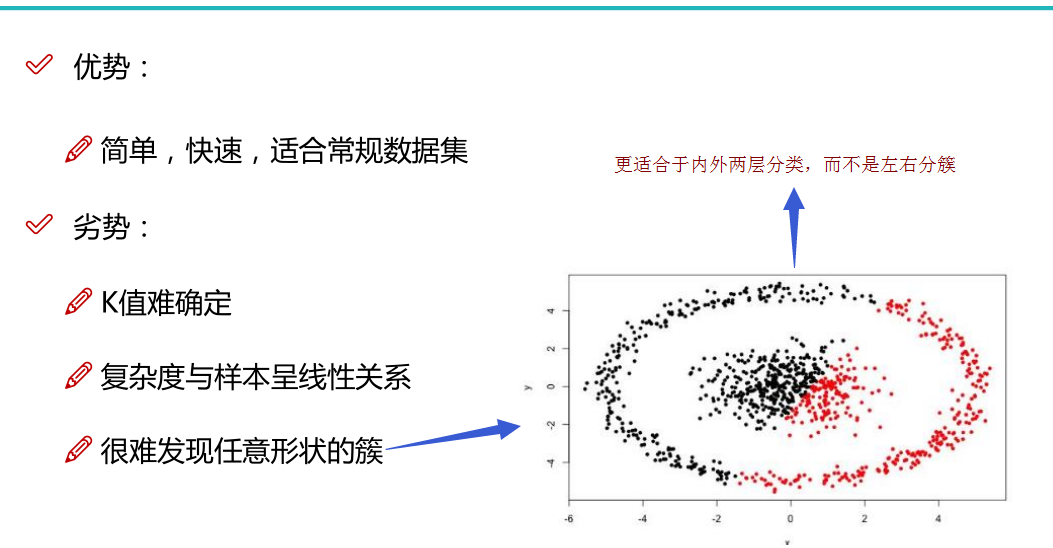
 K-means算法对随机选取 K个初始点作为初始值是很敏感的，结果非常依赖初始值

使用Kmeans进行图像压缩：

# -*- coding: utf-8 -*-

from skimage import io
from sklearn.cluster import KMeans
import numpy as np

image = io.imread('test2.jpg')
io.imshow(image)
io.show()

#查看像素点
rows = image.shape[0]#行数h
cols = image.shape[1]#列数w
#c指的是颜色通道 
image = image.reshape(image.shape[0]*image.shape[1],3)#彩色图像三维：h*w*c    reshape成2维：h*w，c
kmeans = KMeans(n_clusters = 128, n_init=10, max_iter=200)#n_clusters指的是簇的个数，别的可以不用管，也可以不指定
kmeans.fit(image)#fit数据

clusters = np.asarray(kmeans.cluster_centers_,dtype=np.uint8) 
labels = np.asarray(kmeans.labels_,dtype=np.uint8 )  
labels = labels.reshape(rows,cols);#reshape回去，变成二维图像（灰度图）

print (clusters.shape)
np.save('codebook_test.npy',clusters)    
io.imsave('compressed_test.jpg',labels)#压缩后的图像，原来的三通道变为1通道，原来的取值0-265，现在只能为0-128

test2.jpg：

(128, 3)

image = io.imread('compressed_test.jpg')
io.imshow(image)
io.show()

 

 

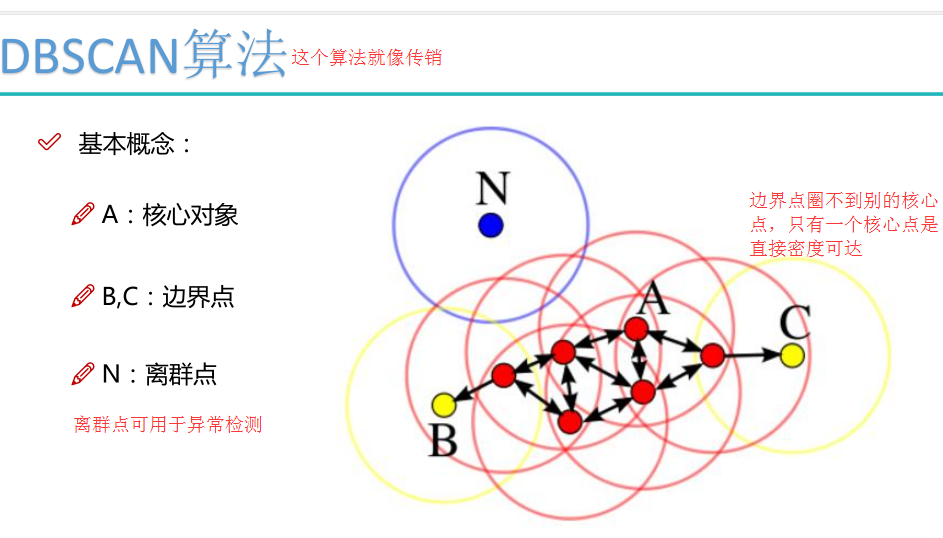
 DBSCAN聚类使用到一个k-距离的概念，k-距离是指：给定数据集P={p(i); i=0,1,…n}，对于任意点P(i)，计算点P(i)到集合D的子集S={p(1), p(2), …, p(i-1), p(i+1), …, p(n)}中所有点之间的距离，距离按照从小到大的顺序排序，假设排序后的距离集合为D={d(1), d(2), …, d(k-1), d(k), d(k+1), …,d(n)}，则d(k)就被称为k-距离。也就是说，k-距离是点p(i)到所有点（除了p(i)点）之间距离第k近的距离。对待聚类集合中每个点p(i)都计算k-距离，最后得到所有点的k-距离集合E={e(1), e(2), …, e(n)}。

根据经验计算最少点的数量MinPts：确定MinPts的大小，实际上也是确定k-距离中k的值，如DBSCAN算法取k=4，则MinPts=4。

离群点如果想多一点，可以减小半径r和MinPts。

MinPts设置大了，簇的个数会变少。