哈夫曼

一、哈夫曼树的概念和定义

 

什么是哈夫曼树？

让我们先举一个例子。

判定树：

        在很多问题的处理过程中，需要进行大量的条件判断，这些判断结构的设计直接影响着程序的执行效率。例如，编制一个程序，将百分制转换成五个等级输出。大家可能认为这个程序很简单，并且很快就可以用下列形式编写出来：

    if(score<60) 
        cout<<"Bad"<<endl; 
    else if(score<70) 
        cout<<"Pass"<<endl 
    else if(score<80) 
        cout<<"General"<<endl; 
    else if(score<90) 
        cout<<"Good"<<endl; 
    else 
        cout<<"Very good!"<<endl; 

若考虑上述程序所耗费的时间，就会发现该程序的缺陷。在实际中，学生成绩在五个等级上的分布是不均匀的。当学生百分制成绩的录入量很大时，上述判定过程需要反复调用，此时程序的执行效率将成为一个严重问题。

 

但在实际应用中，往往各个分数段的分布并不是均匀的。下面就是在一次考试中某门课程的各分数段的分布情况：

 

下面我们就利用哈夫曼树寻找一棵最佳判定树，即总的比较次数最少的判定树。

第一种构造方式：

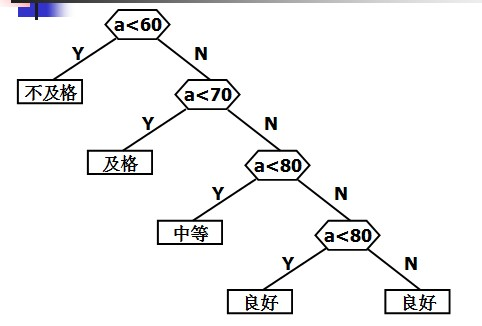
第二种构造方式：

这两种方式，显然后者的判定过程的效率要比前者高。在也没有别地判定过程比第二种方式的效率更高。

 我们称判定过程最优的二叉树为哈夫曼树，又称最优二叉树

 

定义哈夫曼树之前先说明几个与哈夫曼树有关的概念：

• 路径： 树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。

• 路径长度：路径上的分枝数目称作路径长度。

• 树的路径长度：从树根到每一个结点的路径长度之和。

• 结点的带权路径长度：在一棵树中，如果其结点上附带有一个权值，通常把该结点的路径长度与该结点上的权值 之积称为该结点的带权路径长度（weighted path length）
• 权值就是定义的路径上面的值。可以这样理解为节点间的距离。通常指字符对应的二进制编码出现的概率。至于霍夫曼树中的权值可以理解为：权值大表明出现概率大！一个结点的权值实际上就是这个结点子树在整个树中所占的比例.

• 树的带权路径长度：如果树中每个叶子上都带有一个权值，则把树中所有叶子的带权路径长度之和称为树的带权路径长度。

 

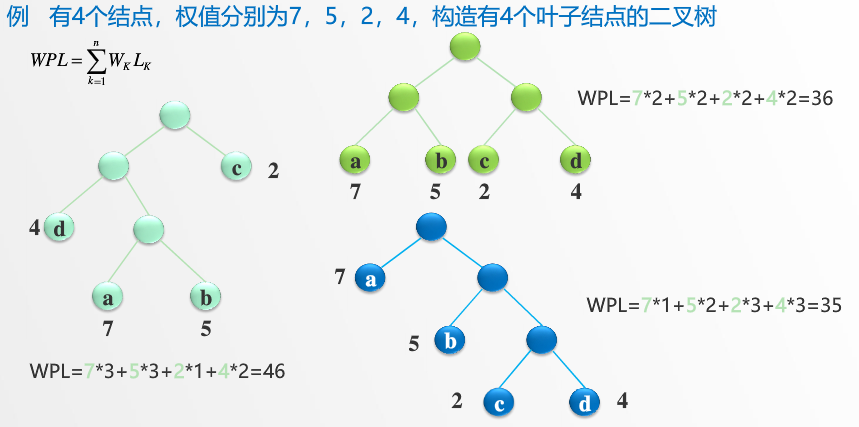
设某二叉树有n个带权值的叶子结点，则该二叉树的带权路径长度记为：

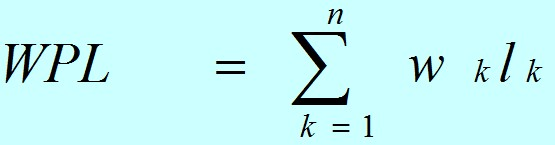（公式中，W_k为第k个叶子结点的权值；L_k为该结点的路径长度。）

 

 

一般来说，用n（n>0）个带权值的叶子来构造二叉树，限定二叉树中除了这n个叶子外只能出现度为2的结点。那么符合这样条件的二叉树往往可构造出许多颗，其中带权路径长度最小的二叉树就称为哈夫曼树或最优二叉树。

 

二、哈夫曼树的构造

 

根据哈弗曼树的定义，一棵二叉树要使其WPL值最小，必须使权值越大的叶子结点越靠近根结点，而权值越小的叶子结点越远离根结点。

 

哈弗曼依据这一特点提出了一种构造最优二叉树的方法，其基本思想如下：

注意：哈夫曼树并不唯一，但带权路径长度一定是相同的。

下面演示了用Huffman算法构造一棵Huffman树的过程：

（1）8个结点的权值大小如下：

（2）从19，21，2，3，6，7，10，32中选择两个权小结点。选中2，3。同时算出这两个结点的和5。

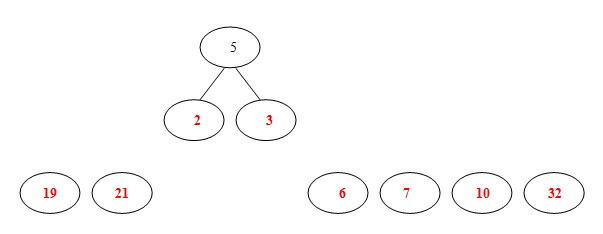
（3）从19，21，6，7，10，32，5中选出两个权小结点。选中5，6。同时计算出它们的和11。

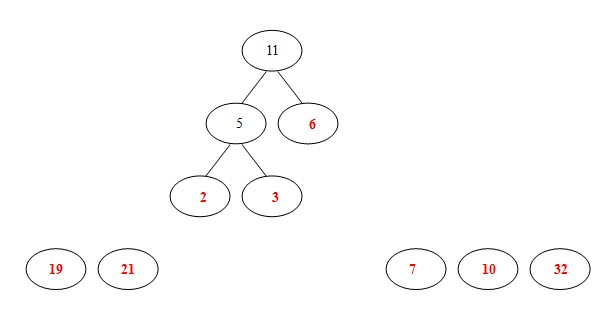
（4）从19，21，7，10，32，11中选出两个权小结点。选中7，10。同时计算出它们的和17。
（BTW：这时选出的两个数字都不是已经构造好的二叉树里面的结点，所以要另外开一棵二叉树；或者说，如果两个数的和正好是下一步的两个最小数的其中的一个，那么这个树直接往上生长就可以了，如果这两个数的和比较大，不是下一步的两个最小数的其中一个，那么就并列生长。）

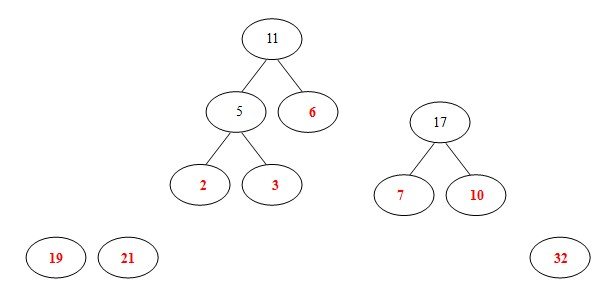
（5）从19，21，32，11，17中选出两个权小结点。选中11，17。同时计算出它们的和28。

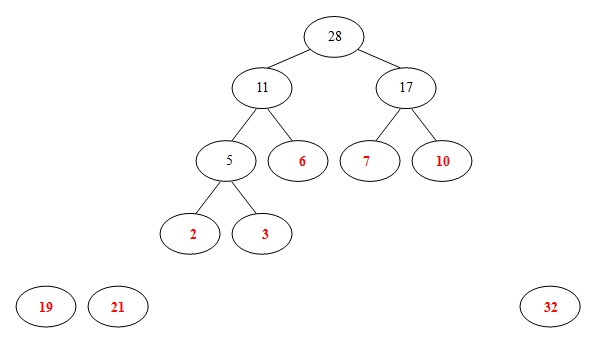
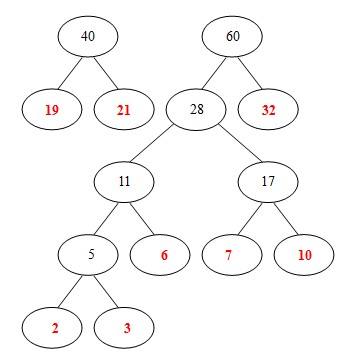
（6）从19，21，32，28中选出两个权小结点。选中19，21。同时计算出它们的和40。另起一颗二叉树。

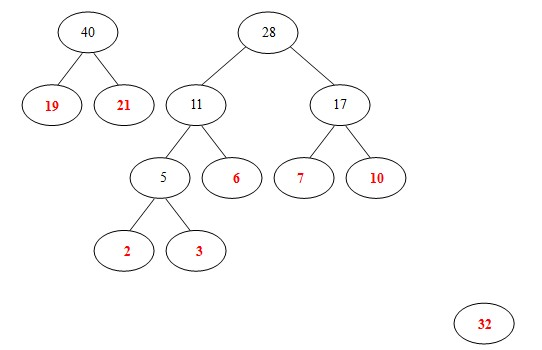
（7）从32，28， 40中选出两个权小结点。选中28，32。同时计算出它们的和60。  

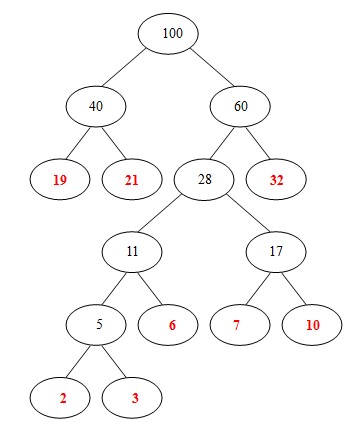
（8）从 40， 60中选出两个权小结点。选中40，60。同时计算出它们的和100。 好了，此时哈夫曼树已经构建好了。

 哈夫曼树又称为最优二叉树，它的节点总数和二叉树相同为2n-1，n为叶子节点个数。

 

 

三、哈夫曼树的在编码中的应用

 

在电文传输中，需要将电文中出现的每个字符进行二进制编码。在设计编码时需要遵守两个原则：

（1）发送方传输的二进制编码，到接收方解码后必须具有唯一性，即解码结果与发送方发送的电文完全一样；

（2）发送的二进制编码尽可能地短。下面我们介绍两种编码的方式。

 

1. 等长编码

            这种编码方式的特点是每个字符的编码长度相同（编码长度就是每个编码所含的二进制位数）。假设字符集只含有4个字符A，B，C，D，用二进制两位表示的编码分别为00，01，10，11。若现在有一段电文为：ABACCDA，则应发送二进制序列：00010010101100，总长度为14位。当接收方接收到这段电文后，将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性，但编码长度并不是最短的。

 

2. 不等长编码

            在传送电文时，为了使其二进制位数尽可能地少，可以将每个字符的编码设计为不等长的，使用频度较高的字符分配一个相对比较短的编码，使用频度较低的字符分配一个比较长的编码。例如，可以为A，B，C，D四个字符分别分配0，00，1，01，并可将上述电文用二进制序列：000011010发送，其长度只有9个二进制位，但随之带来了一个问题，接收方接到这段电文后无法进行译码，因为无法断定前面4个0是4个A，1个B、2个A，还是2个B，即译码不唯一，因此这种编码方法不可使用。

 

因此，为了设计长短不等的编码，以便减少电文的总长，还必须考虑编码的唯一性，即在建立不等长编码时必须使任何一个字符的编码都不是另一个字符的前缀，这宗编码称为前缀编码（prefix  code）

 

（1）利用字符集中每个字符的使用频率作为权值构造一个哈夫曼树；

（2）从根结点开始，为到每个叶子结点路径上的左分支赋予0，右分支赋予1，并从根到叶子方向形成该叶子结点的编码

 

例题：

假设一个文本文件TFile中只包含7个字符{A，B，C，D，E，F，G}，这7个字符在文本中出现的次数为{5，24，7，17，34，5，13}

利用哈夫曼树可以为文件TFile构造出符合前缀编码要求的不等长编码

 

具体做法：

 

1. 将TFile中7个字符都作为叶子结点，每个字符出现次数作为该叶子结点的权值

2. 规定哈夫曼树中所有左分支表示字符0，所有右分支表示字符1,将依次从根结点到每个叶子结点所经过的分支的二进制位的序列作为该

     结点对应的字符编码

3. 由于从根结点到任何一个叶子结点都不可能经过其他叶子，这种编码一定是前缀编码，哈夫曼树的带权路径长度正好是文件TFile编码

    的总长度

 

通过哈夫曼树来构造的编码称为哈弗曼编码（huffman code）

参考：https://www.cnblogs.com/13224ACMer/p/4706174.html