ROC曲线的绘制

假设现在有一个二分类问题，先引入两个概念：

• 真正例率（TPR）：正例中预测为正例的比例
• 假正例率（FPR）：反例中预测为正例的比例

再假设样本数为6，现在有一个分类器1，它对样本的分类结果如下表（按预测值从大到小排序）

 

 

 

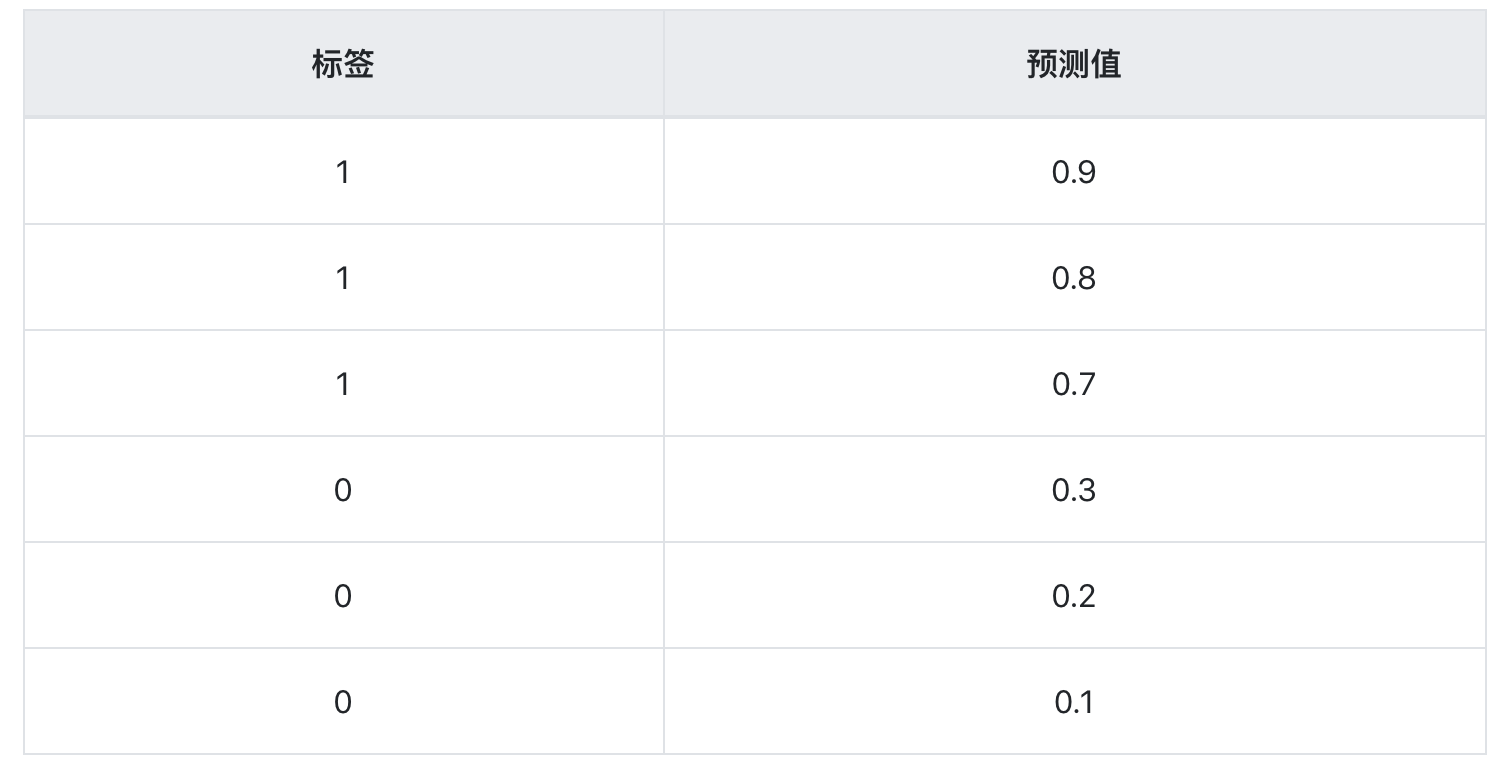
ROC曲线的横轴为假正例率，纵轴为真正例率，范围都是[0,1]，现在我们开始画图——根据从大到小遍历预测值，把当前的预测值当做阈值，计算FPR和TPR。

step1：选择阈值最大，即为1，正例中和反例中都没有预测值大于等于1的，所以FPR=TPR=0。

step2：根据上表，选择阈值为0.9，正例中有1个样本的预测值大于等于1，反例中有0个，所以，TPR=1/3，FPR=0。

step3：根据上表，选择阈值为0.8，正例中有2个样本的预测值大于等于1，反例中有0个，所以，TPR=2/3，FPR=0。

step4：根据上表，选择阈值为0.7，正例中有3个样本的预测值大于等于1，反例中有0个，所以，TPR=1，FPR=0。

step5：根据上表，选择阈值为0.3，正例中有3个样本的预测值大于等于1，反例中有1个，所以，TPR=1，FPR=1/3。

step6：根据上表，选择阈值为0.2，正例中有3个样本的预测值大于等于1，反例中有2个，所以，TPR=1，FPR=2/3。

step7：根据上表，选择阈值为0.1，正例中有3个样本的预测值大于等于1，反例中有3个，所以，TPR=1，FPR=1。

综上，我们得到下表：

 

 

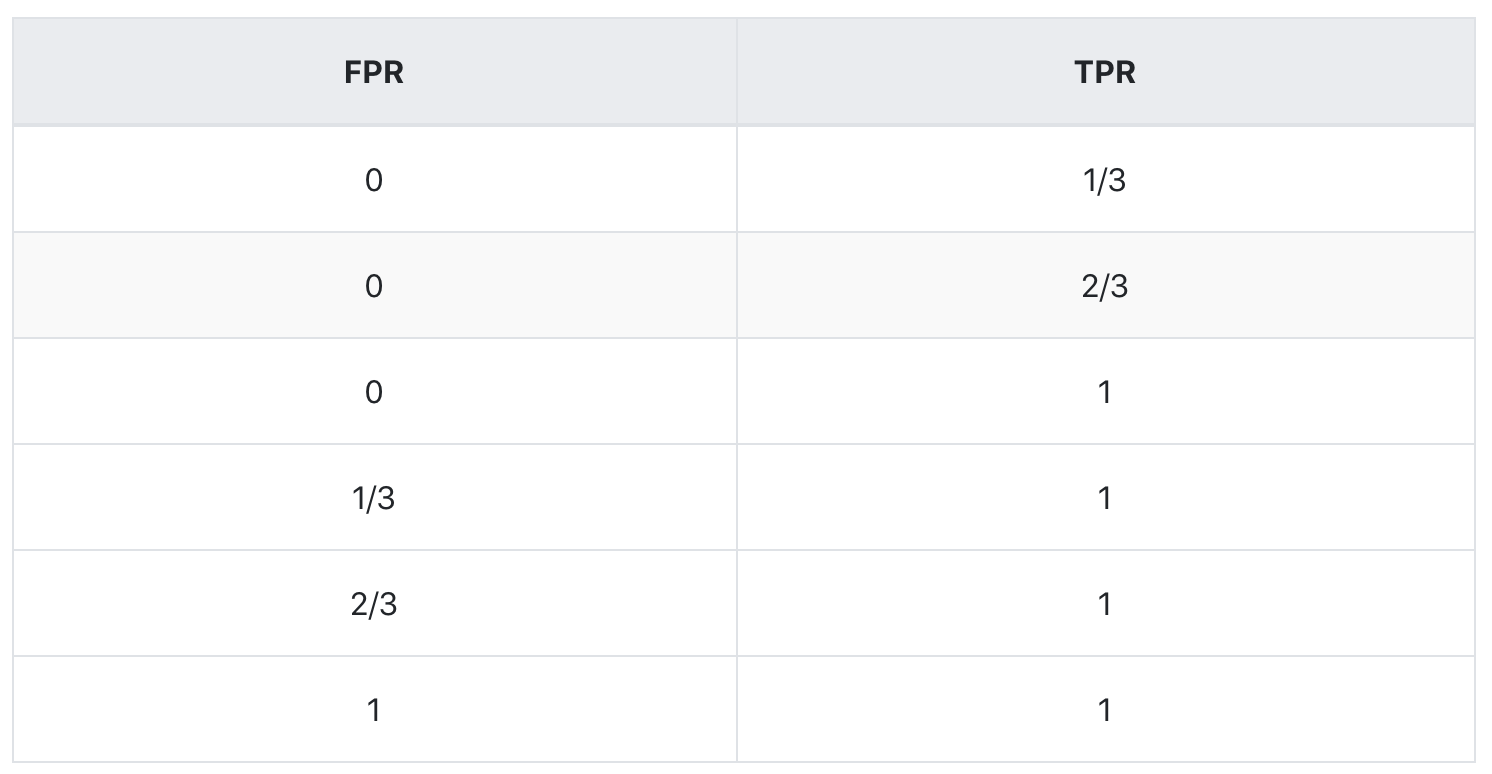
描点连线，画出的图是下面这样什儿的

 

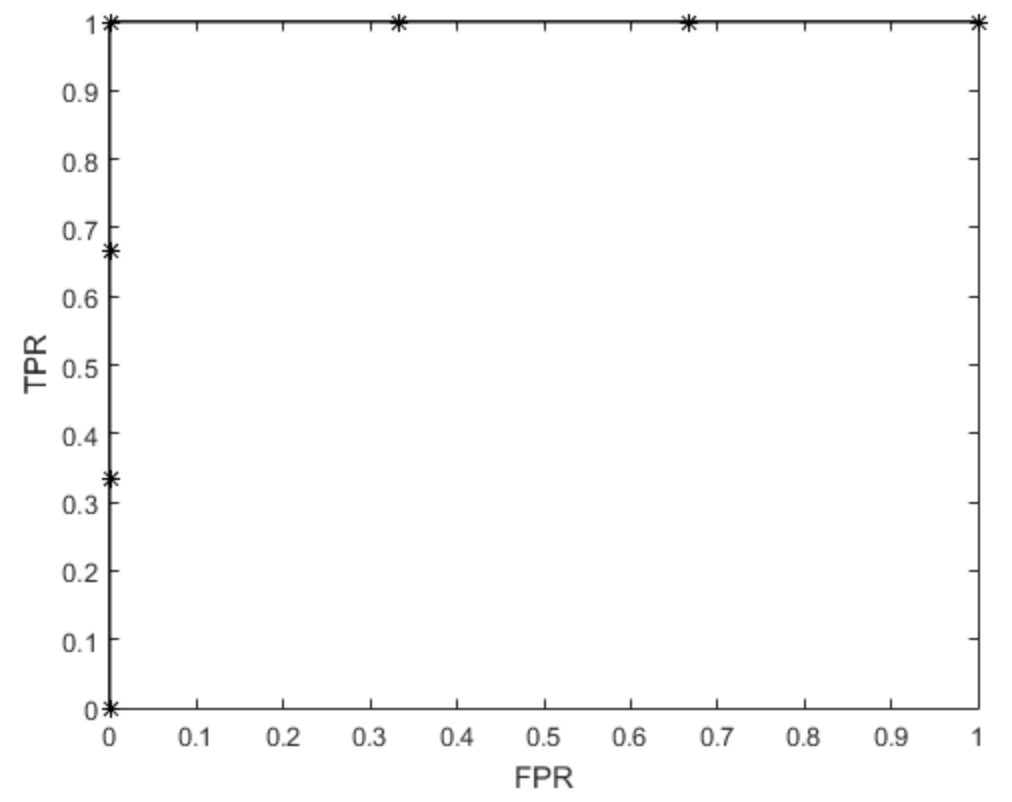
可以看出这个分类器还是很理想的。

假设现在又有一个分类器2，对同样一组样本，分类结果如下

 

 

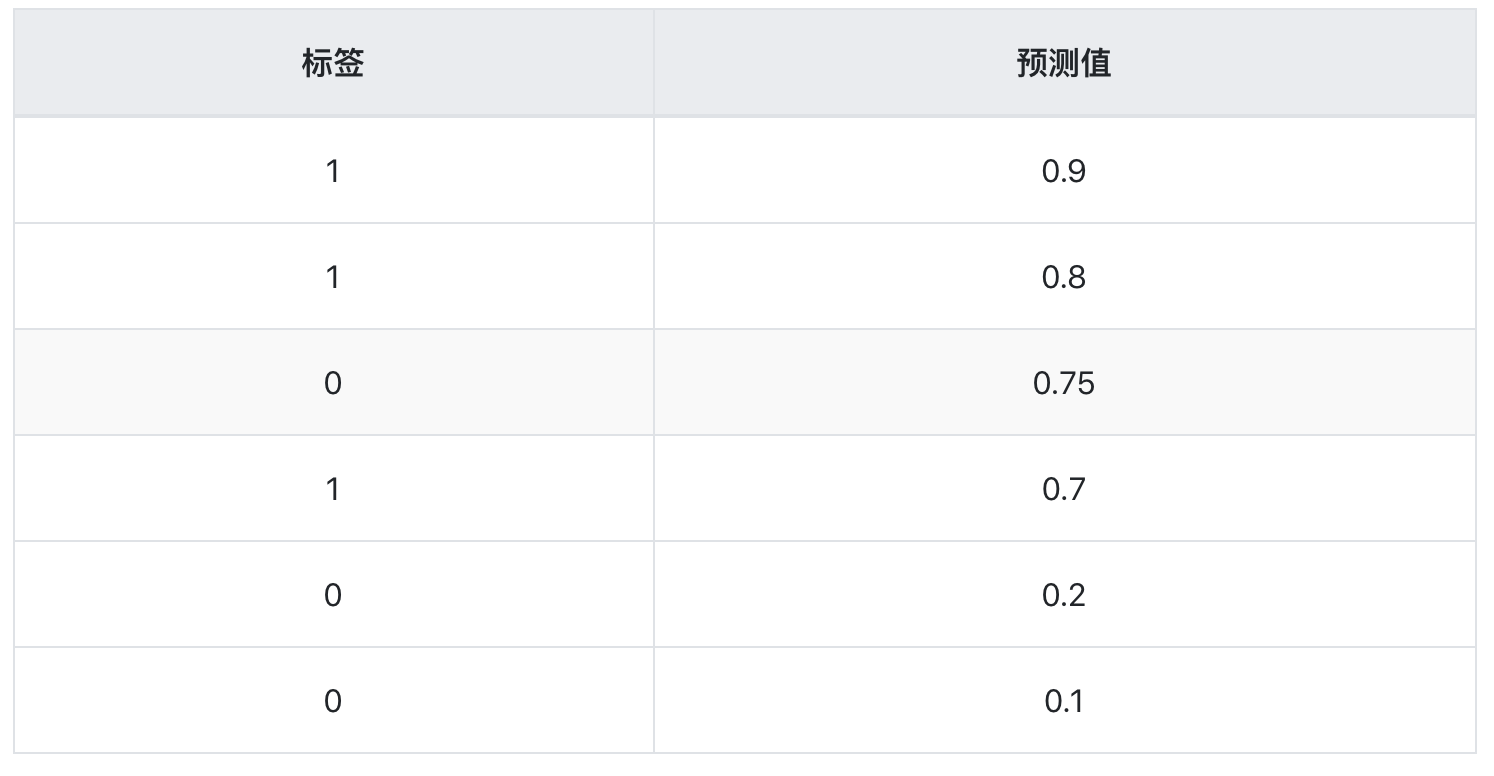
 根据上面描述的方法，画出ROC曲线如下

 

 

 

发现这个曲线的左上角比之前往右下角凹了一点。

emmmm，现在又来了一个分类器3，对同样一组样本，分类结果如下

 

 

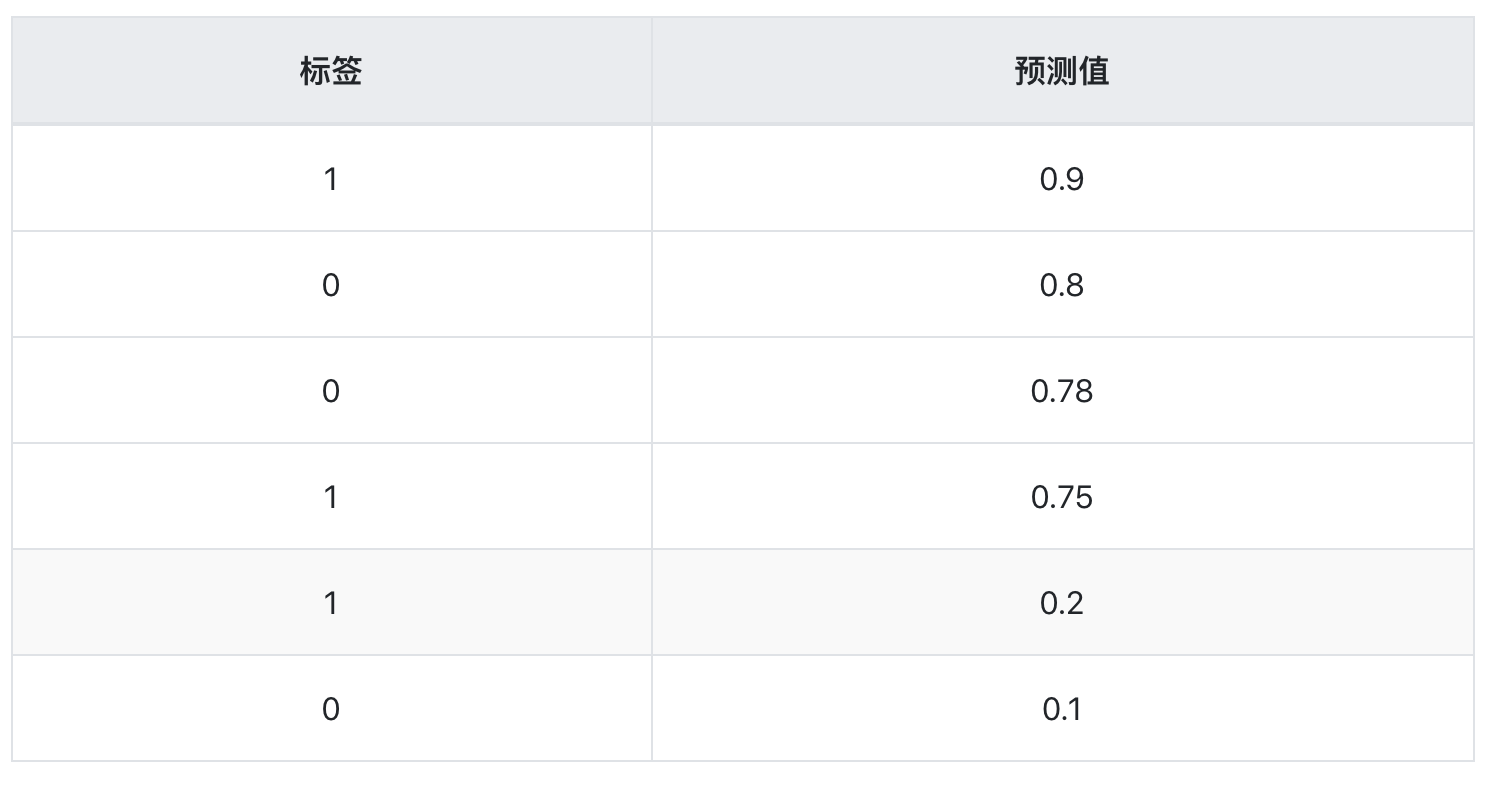
 不多说，直接画图——

 

 

 

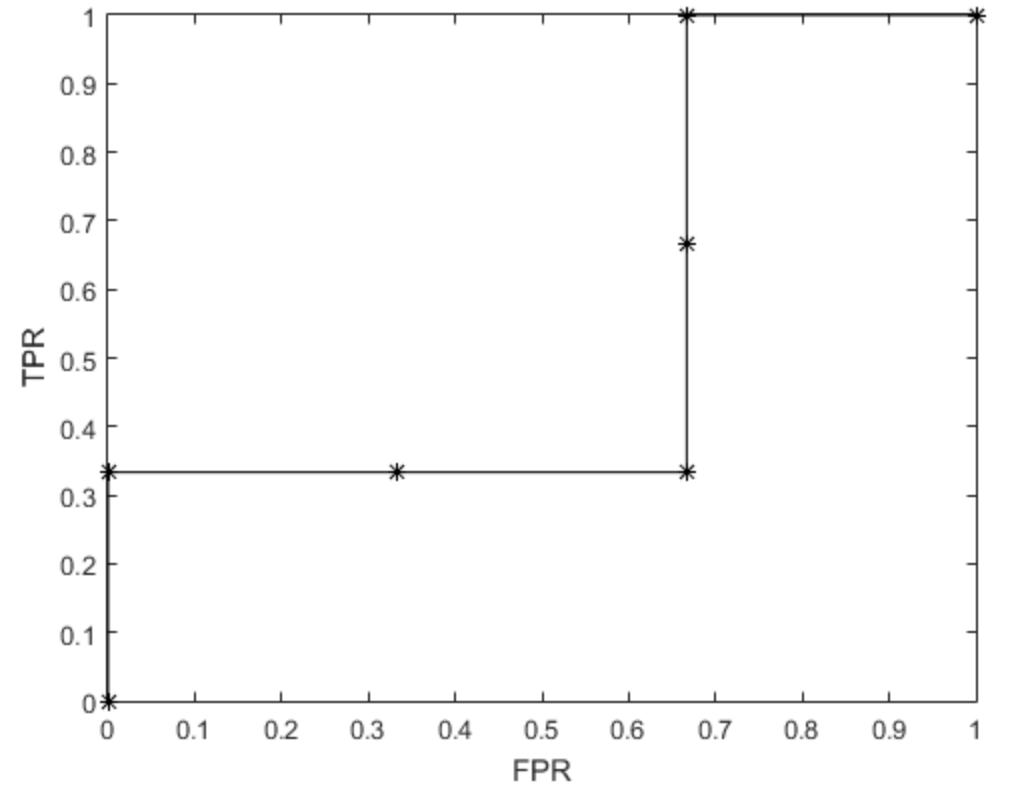
哎？这个曲线比之前更“凹”了。

实际上，不用画出曲线，只是根据这3个分类器的分类结果，我们也能大概能分析出它们的性能：分类器1>分类器2>分类器3。

对分类器1的预测结果来说，所有的正例的预测值都在1这一侧，所有反例的预测值都在0那一侧，只要阈值取得合适，即阈值落在(0.3,0.7)内都可以。

再看分类器2的预测结果，出现了对反例的预测值（0.75）大于对正例的预测值了（0.7），所以不能选择一个合适的阈值把这两类完全分开，所以反映在图上就是左上角凹了一点，但对大部分样本还是可以正确分类的。

再看分类器3的预测结果，这种不稳定性就更明显了，所以相比前两个的ROC曲线，凹得就更多了。

从这个角度，也就不难得出，ROC下面的面积越大，分类器越好的结论了。当然还有严格的数学角度的分析，感兴趣的，了解一下。

下面附上画图用的matlab代码

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

clear; clc; % 分类器1 % label = [1,1,1,0,0,0]; % predict = [0.9,0.8,0.7,0.3,0.2,0.1];   % 分类器2 % label = [1,1,0,1,0,0]; % predict = [0.9,0.8,0.75,0.7,0.2,0.1];   % 分类器3 label = [1,0,0,1,1,0]; predict = [0.9,0.8,0.78,0.75,0.2,0.1];     TPR=[]; FPR=[]; numPositive = size(find(label==1),2); numNegative = size(find(label==0),2); postive = predict(find(label==1)); negative = predict(find(label==0)); for i=1:size(label,2)+1     if i==1         cur = 1;     else         cur = predict(i-1);     end     TPR(i) = size(find(postive>=cur),2)/numPositive;     FPR(i) = size(find(negative>=cur),2)/numNegative; end plot(FPR,TPR,'k*-') axis([0 1 0 1]); xlabel('FPR') ylabel('TPR')

　　源自：https://segmentfault.com/a/1190000016735657