HDU1024-最大子段和
题意:给N个数 然后把这些数分成M段 求子段和的最大值
思路:不难去想 我们用dp[i][j]去表示前面j个数分成了i段的最大值 那么就会出现一个问题 那就是第j个数是不是在这i段之内 (1) 我们把第J个数放在前i段内 那么显然 dp[i][j]=dp[i][j-1]+a[j] (2) 我们让第j个数去一个新段 那个前j-1个数就只能分成i-1段 因为我们让第j个数成了第i段 那这个时候 dp[i][j]=dp[i-1][j-1]+a[j]? 显然不是的
这个时候我们需要去枚举第i-1个元素到底j-1个元素中分成i-1段的值 然后去找最大值
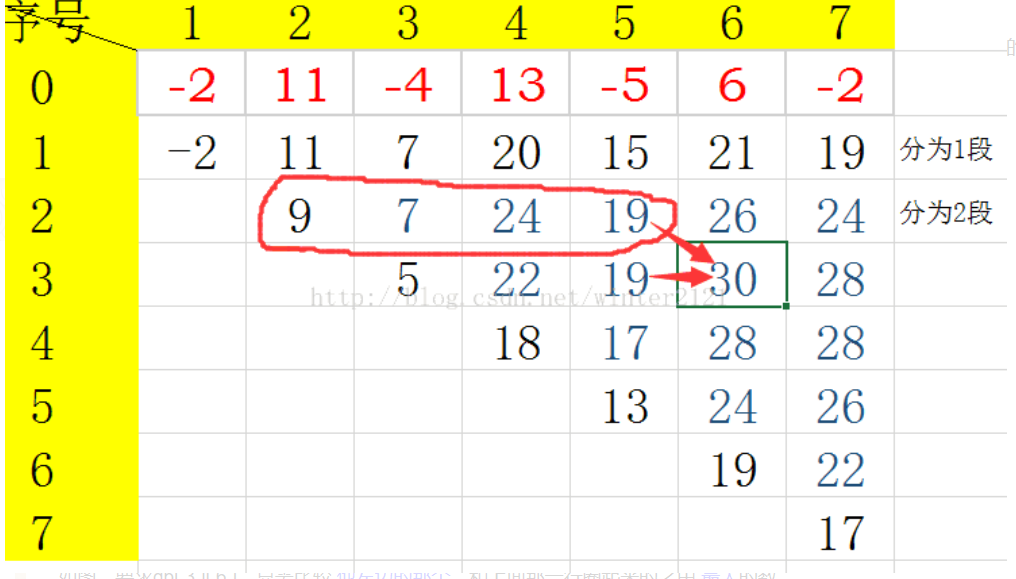
看了网上一个大佬用的矩阵图 我们可以清楚的看到dp[3][6]的值就是他左边的那个数和画圈的那个数中的最大值加上a[6] 这个时候我们就可以发现dp[i][j]其实等于dp[i][j-1]和上一行中数的最大值再去加上a[j] 所以 状态方程可以得到dp[i][j]=max(dp[i][j-1]+a[j],max(dp[i-1][k]+a[k])) (i-1<=k<j-1)
这个时候就会发现 这么写的话肯定凉凉 那么就要想办法优化一下 其实我们想得简单一点 我们完全可以把在求max(dp[i-1][k]+a[k])的值用一个数组给存起来 等到用的时候直接查不就行了 所以 我们直接用dp[i]来代表前i个数分为m段的最大值 那个 dp1[i]=max(dp1[i-1]+a[i],dp2[i-1]+a[i]) 具体看代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+6;
const int inf=0x3f3f3f3f;
int a[maxn],dp1[maxn],dp2[maxn];
int main()
{
int m,n;
while(~scanf("%d %d",&m,&n))
{
int ans;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
dp1[i]=0;
dp2[i]=0;
}
for(int i=1;i<=m;i++)
{
ans = -inf;
for(int j=i;j<=n;j++)
{
dp1[j]=max(dp1[j-1]+a[j],dp2[j-1]+a[j]);
dp2[j-1]=ans;
ans=max(ans,dp1[j]);
}
}
cout<<ans<<endl;
}
return 0;
}

