深入浅出WPF变换(Transform)之矩阵(Matrix)

背景知识

Matrix是一个用于在二维坐标系中进行坐标转换的3*3仿射变换矩阵。
什么是仿射变换？为什么是3*3，不是2*2？好的，让我们来复习一下（以下内容来自百度百科）：

仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。仿射变换是在几何上定义为两个向量空间之间的一个仿射变换或者仿射映射（来自拉丁语，affine，“和…相关”）由一个非奇异的线性变换(运用一次函数进行的变换)接上一个平移变换组成。
在有限维的情况，每个仿射变换可以由一个矩阵A和一个向量b给出，它可以写作A和一个附加的列b。一个仿射变换对应于一个矩阵和一个向量的乘法，而仿射变换的复合对应于普通的矩阵乘法，只要加入一个额外的行到矩阵的底下，这一行全部是0除了最右边是一个1，而列向量的底下要加上一个1。

一般定义
一个对向量x平移b，与旋转、放大/缩小A的仿射映射为

 

上式在齐次坐标上，等价于下面的式子

与上述背景知识中的描述不同的是，Matrix中使用的是行向量，而非列向量（这一点，MSDN中有说明，我也会在下文中进行验证），这一变化也导致上式变为：

即

 

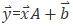
属性

 Matrix虽是3*3矩阵，但其中可以进行设定的矩阵元素只有6个，分别是：M11, M12, M21,M22和OffsetX、OffsetY，如下，

即增广列0,…,0, 1不可修改。Matrix中以属性的形式将这些元素暴露给外界。其中M11,M22影响缩放，OffsetX,OffsetY影响平移，M12,M21(和M11，M22)一起影响旋转等。

方法

Matrix暴露了以下方法（只列出了和变换相关的）：

方法签名	说明
Append(Matrix)	将指定的Matrix结构追加到此Matrix结构。
Invert()	反转此 Matrix 结构。
Multiply(Matrix, Matrix)	让 Matrix 结构乘以另一个 Matrix 结构。
Prepend(Matrix)	将指定的 Matrix 结构添加到此 Matrix 结构之前。
Rotate(Double)	以此 Matrix 结构的原点为中心旋转指定的角度。
RotateAt(Double, Double, Double)	绕指定的点旋转此矩阵。
RotateAtPrepend(Double, Double, Double)	在此 Matrix 结构前面添加围绕指定点的指定角度的旋转。
RotatePrepend(Double)	在此 Matrix 结构前面添加指定角度的旋转。
Scale(Double, Double)	在此 Matrix 结构后面追加指定的缩放向量。
ScaleAt(Double, Double, Double, Double)	围绕指定的点按指定的量缩放此 Matrix。
ScaleAtPrepend(Double, Double, Double, Double)	在此 Matrix 前面添加围绕指定点的指定缩放。
ScalePrepend(Double, Double)	在此 Matrix 结构前面添加指定的缩放向量。
SetIdentity()	将此 Matrix 结构更改为恒等矩阵。
Skew(Double, Double)	在此 Matrix 结构后面追加 x 和 y 维中指定角度的扭曲。
SkewPrepend(Double, Double)	在此 Matrix 结构前面添加 x 和 y 维中指定角度的扭曲。
Transform(Point)	用 Matrix 变换指定的点并返回结果。
Transform(Point[])	用此 Matrix 变换指定的点。
Transform(Vector)	用此 Matrix 变换指定的向量。
Transform(Vector[])	用此 Matrix 变换指定的向量。
Translate(Double, Double)	在此 Matrix 结构后面追加指定偏移量的平移。
TranslatePrepend(Double, Double)	在此 Matrix 结构前面添加指定偏移量的平移。

下面以部分方法为例，让我们来看一看Matrix是如何实现转换的：

1.旋转变换（Rotate）

RotateAt：以某点为中心点进行旋转变换。其实现如下：

public void RotateAt(double angle, double centerX, double centerY)
{
　　angle %= 360.0;
　　this *= CreateRotationRadians(angle * (Math.PI / 180.0), centerX, centerY);
}
internal static Matrix CreateRotationRadians(double angle, double centerX, double centerY)
{
　　Matrix result = default(Matrix);
　　double num = Math.Sin(angle);
　　double num2 = Math.Cos(angle);
　　double offsetX = centerX * (1.0 - num2) + centerY * num;
　　double offsetY = centerY * (1.0 - num2) - centerX * num;
　　result.SetMatrix(num2, num, 0.0 - num, num2, offsetX, offsetY, MatrixTypes.TRANSFORM_IS_UNKNOWN);
　　return result;
}

 CreateRotationRadians方法通过一系列计算产生了一个用于旋转的Matrix（以下简称“矩阵R”），

这一些列计算是怎么来的呢？不妨让我们再来回顾下坐标旋转的知识。

有式①

X - X₀ = r*cos(α)

Y - Y₀ = r*sin(α)

式②，

X’ - X₀ = r*cos(α-θ) = r*[cos(α)*cos(θ) + sin(α)*sin (θ)]

Y’ - Y₀ = r*sin(α-θ) = r*[sin(α)*cos(θ) - cos(α)*sin(θ)]

将式①代入式②得到：

X’ - X₀ = (X- X₀)* cos(θ) + (Y- Y₀)* sin(θ)

Y’ - Y₀ = (Y- Y₀)* cos(θ) – (X- X₀)* sin(θ)

即，

X’= (X - X₀)* cos(θ) + (Y - Y₀)* sin(θ) + X₀ = X*cos(θ) + Y*sin(θ) + X₀*[1- cos(θ)] - Y₀*sin(θ)

Y’= (Y - Y₀)* cos(θ) – (X - X₀)* sin(θ) + Y₀ = –X*sin(θ) + Y*cos(θ) + Y₀*[1- cos(θ)] + X₀*sin(θ)

首先，来确定行向量还是列向量的问题。按照背景知识中提到的，如果是列向量，那么会有：

但这明显与CreateRotationRadians中计算出的矩阵R不一样，对比下可以发现，它们似乎是转置的关系：

矩阵R

令

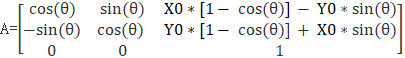
那么A的转置矩阵

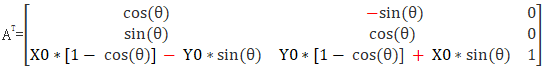
A转置后，需要将列向量转置，并左乘A^T才能满足等式成立，即，

至此，我们通过RotateAt方法产生的旋转矩阵R，验证了上文提到的WPF Matrix中采用的是行向量的结论。

但还没完。对比矩阵R和A的转置矩阵，可以发现，A的转置矩阵中有4处（M12,M21,OffsetX及OffsetY）正负号与矩阵R不一致（用红色高亮处）。

先看前两处（为了方便查看，下面把前面的计算式重新写了一遍）：

式①

X - X₀ = r*cos(α)

Y - Y₀ = r*sin(α)

式②，

X’ - X₀ = r*cos(α-θ) = r*[cos(α)*cos(θ) + sin(α)*sin (θ)]

Y’ - Y₀ = r*sin(α-θ) = r*[sin(α)*cos(θ) – cos(α)*sin(θ)]

将式①代入式②得到：

X’ - X₀= (X - X₀)* cos(θ) + (Y - Y₀)* sin(θ) 　　// 引入了M21的正负号

Y’ - Y₀= (Y - Y₀)* cos(θ) – (X - X₀)* sin(θ) 　　// 引入了M12的正负号

因为两个矩阵元素的绝对值一致，只是正负号相反，而且从上述引入M12和M21的正负号的地方可以推出，正负号的异常是因为计算角度(α-θ)导致，如果改成(α+θ)，我们再来计算一遍：

式③，

X’ - X₀= r*cos(α+θ) = r*[cos(α)*cos(θ) – sin(α)*sin (θ)]

Y’ - Y₀= r*sin(α+θ) = r*[sin(α)*cos(θ) + cos(α)*sin(θ)]

将式①代入式③得到：

X’ - X₀= (X - X₀)*cos(θ) – (Y - Y₀)*sin(θ) = X*cos(θ) - Y*sin(θ) - X₀*cos(θ) + Y₀*sin(θ)

Y’ - Y₀= (Y - Y₀)*cos(θ) + (X - X₀)*sin(θ) = X*sin(θ) + Y*cos(θ) - Y₀*cos(θ) - X₀*sin(θ)

即，

X’= X*cos(θ) - Y*sin(θ) + X₀*[1-cos(θ)] + Y₀*sin(θ)

Y’= X*sin(θ) + Y*cos(θ) + Y₀*[1-cos(θ)] - X₀*sin(θ)

与矩阵R完全一致。那么问题来了，顺时针旋转角度θ，为什么向量（X’,Y’）的角度会是(α+θ)呢？是的，你想到了，WPF中运算的坐标系是右下（x-y）方向，而不是右上（x-y），即，

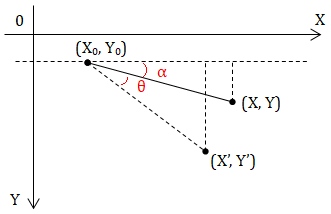
好了，稍微总结一下：

1.Matrix中使用的是行向量，因此其转换公式是 ；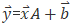

2.Matrix运算是基于右下方向的x-y坐标系，而非右上方向。

2.缩放变换（Scale）

ScaleAt:以某点为原点进行缩放变换，其实现如下：

public void ScaleAt(double scaleX, double scaleY, double centerX, double centerY)
{
    this *= CreateScaling(scaleX, scaleY, centerX, centerY);
}
internal static Matrix CreateScaling(double scaleX, double scaleY, double centerX, double centerY)
{
    Matrix result = default(Matrix);
    result.SetMatrix(scaleX, 0.0, 0.0, scaleY, centerX - scaleX * centerX, centerY - scaleY * centerY, MatrixTypes.TRANSFORM_IS_TRANSLATION | MatrixTypes.TRANSFORM_IS_SCALING);
    return result;
}

 

如上图1，以(X₀, Y₀)为原点，对点(X, Y)进行缩放，得到点(X’, Y’)。可以计算出x,y轴的缩放因子：

Fx = (X’- X₀)/ (X- X₀)

Fy = (Y’- Y₀)/ (Y- Y₀)

即，

X’ = Fx*X + X₀ – Fx* X₀

F’ = Fy*Y + Y₀ – Fy* Y₀

与上述CreateScaling中计算得到的各项系数一致。

3.倾斜变换（Skew）

Skew：扭曲/倾斜变换。其实现如下：

 1 public void Skew(double skewX, double skewY)
 2 {
 3     skewX %= 360.0;
 4     skewY %= 360.0;
 5     this *= CreateSkewRadians(skewX * (Math.PI / 180.0), skewY * (Math.PI / 180.0));
 6 }
 7 internal static Matrix CreateSkewRadians(double skewX, double skewY)
 8 {
 9     Matrix result = default(Matrix);
10     result.SetMatrix(1.0, Math.Tan(skewY), Math.Tan(skewX), 1.0, 0.0, 0.0, MatrixTypes.TRANSFORM_IS_UNKNOWN);
11     return result;
12 }

注意Skew方法中的两个参数的意义，skewX表示沿着X轴正向（如果角度为正）倾斜指定角度，skewY同理。

上图是通过SkewTransform做倾斜变换的效果。可以看到，当沿X轴倾斜时（图2），被转换的点在Y轴的投影是不变的，沿Y轴倾斜也是同样的道理。

通过观察上述图1到图4的变化，可以发现，对x-y坐标系中的向量P做倾斜转换就是将P在X和Y轴的投影分别做指定角度的倾斜，然后进行向量相加。

即，

(X’,Y’)= OM + ON = (X, X*tan(α)) + (Y*tan(θ), Y) = (X + Y*tan(θ), X*tan(α) + Y)

因此可得其转换矩阵为（其中θ=skewX, α=skewY）：

与CreateSkewRadians中产生的矩阵一致。

4.其他

矩阵相乘

public void Append(Matrix matrix)
{
    this *= matrix;
}
public void Prepend(Matrix matrix)
{
    this = matrix * this;
}

就是矩阵左乘还是右乘的区别，更直观的表述就是先执行哪个操作与后执行哪个操作的区别。举例来说，矩阵A是缩放变换矩阵，矩阵B是平移变换矩阵，先执行A和后执行A是不一样的。