归并排序--实现与性能分析

基本思路

在快速排序中我们聊到过分治法，归并排序也是运用了这个思想。

首先定义一个操作，名为「归并」：将两个有序的数组合并成一个更大的有序数组。

我们先忽略「归并」操作是如何实现的，就假定我们已经有了这个操作，来看看如何运用分治法完成归并排序，以数组arr[n]为例说明：

• 分解 ：把有n个元素的待排序的数组，分解为两个子数组，每个数组有n/2个的元素。（两个子数组便是两个子问题）
• 解决：递归地对两个子数组进行归并排序，直到子数组的元素只有1个(有序)，调用「归并」操作:把当前子问题下的两个子数组合并成一个更大的有序数组。
• 合并：合并两个已排序的子序列以产生已排序的答案

PHP代码实现上述例子

function mergeSort(array &$arr) 
{
  $hi = count($arr) - 1;
  mergeSortHandle($arr, 0, $hi);
}

function mergeSortHandle(array &$arr, $lo, $hi) 
{
  if ($lo >= $hi) {
    return;
  }
  $mid = intval(($lo + $hi) / 2);
  mergeSortHandle($arr, $lo, $mid);
  mergeSortHandle($arr, $mid + 1, $hi);
  
  // 归并操作
  merge($arr, $lo, $mid, $hi);
}

归并操作

归并操作的目的是将两个有序数组合并成一个有序数组，具体实现的方法会有很多，这里实现一个原地并归的操作, 函数定义如下：

function merge(array &$arr, $lo, $mid, $hi)

先将数组arr[lo...hi]复制到aux[]中，aux是一个临时数组，作用是存放待排序数组初始元素。 以索引mid为界限，aux中分两个有序子数组：

1. aux[lo...mid], 我们称之为「左子数组」
2. aux[mid+1, lo], 称之为「右子数组」

开始遍历、归并数组：

1. 当左子数组的当前元素大于右子数组当前元素，取左子数组的元素放入arr
2. 当右子数组的当前元素大于左子数组当前元素，取右子数组的元素放入arr
3. 当左子数组已遍历结束，取右子数组的当前元素放入arr
4. 当右子数组已遍历结束，取左子数组的当前元素放入arr

PHP代码实现归并操作

function merge(array &$arr, $lo, $mid, $hi) 
{
  $aux = [];
  for ($k = $lo; $k <= $hi; $k++) {
    $aux[$k] = $arr[$k];
  }
  $i = $lo;
  $j = $mid + 1;
  for ($k = $lo; $k <= $hi; $k++) {
    if ($i > $mid) {
      $arr[$k] = $aux[$j++];
    } elseif ($j > $hi) {
      $arr[$k] = $aux[$i++];
    } elseif ($aux[$i] < $aux[$j]){
      $arr[$k] = $aux[$i++];
    } else{
      $arr[$k] = $aux[$j++];
    }
  }
}

性能

归并排序每次递归都将数组分为两个子数组，也就是二分法。如果画出这颗递归树，树的层数为\(lg n\)。(如果不明白的话，可以看本文结尾关于二分法复杂度的证明)

空间复杂度

归并排序的空间复杂度有两个开销=函数递归栈+临时数组aux

函数递归栈：递归树的层数为\(lg n\)，可得复杂度为\(O(lg n)\)

临时数组：占用的空间与数组的大小成正比，复杂度为O(n)

因此，空间复杂度 = \(O(\log_2n) + O(n)\) = $ O(n)$

时间复杂度

我看观察归并操作的代码，会发现整个操作一共进行了两次数组的遍历，其中都是简单的赋值和比较，可得「结论1」：归并操作的时间复杂度与当前需要排序的元素个数成正比。

我们来看下递归树，n代表数组元素数量：

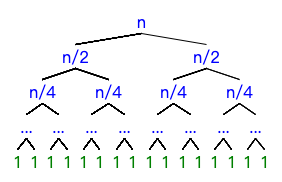
每一层递归中，所有元素加起来的个数刚好为n，根据「结论1」可得每一层递归的归并操作总时间复杂度为\(O(n)\)

在之前的论述中，我们说过归并排序过程中的递归是二分法，递归树的高度是\(\log_2n\)

故可得整体的时间复杂度是：\(O(n\lg n)\)

证明二分法的复杂度为\(O(\log n)\)

二分法每次把序列中的元素减少一半，直到序列中的元素剩下1个。

次数	元素个数
0	\(n\)
1	\(\frac{n}{2}\)
2	\(\frac{n}{2^2}\)
3	\(\frac{n}{2^3}\)
...	...
i	\(\frac{n}{2^i}\)

我们假定第i次为最后一次二分操作，此时有：
\(\frac{n}{2^i}=1\)

\(n = 2 ^ i\)

\(i = \log_2n\)