红黑树

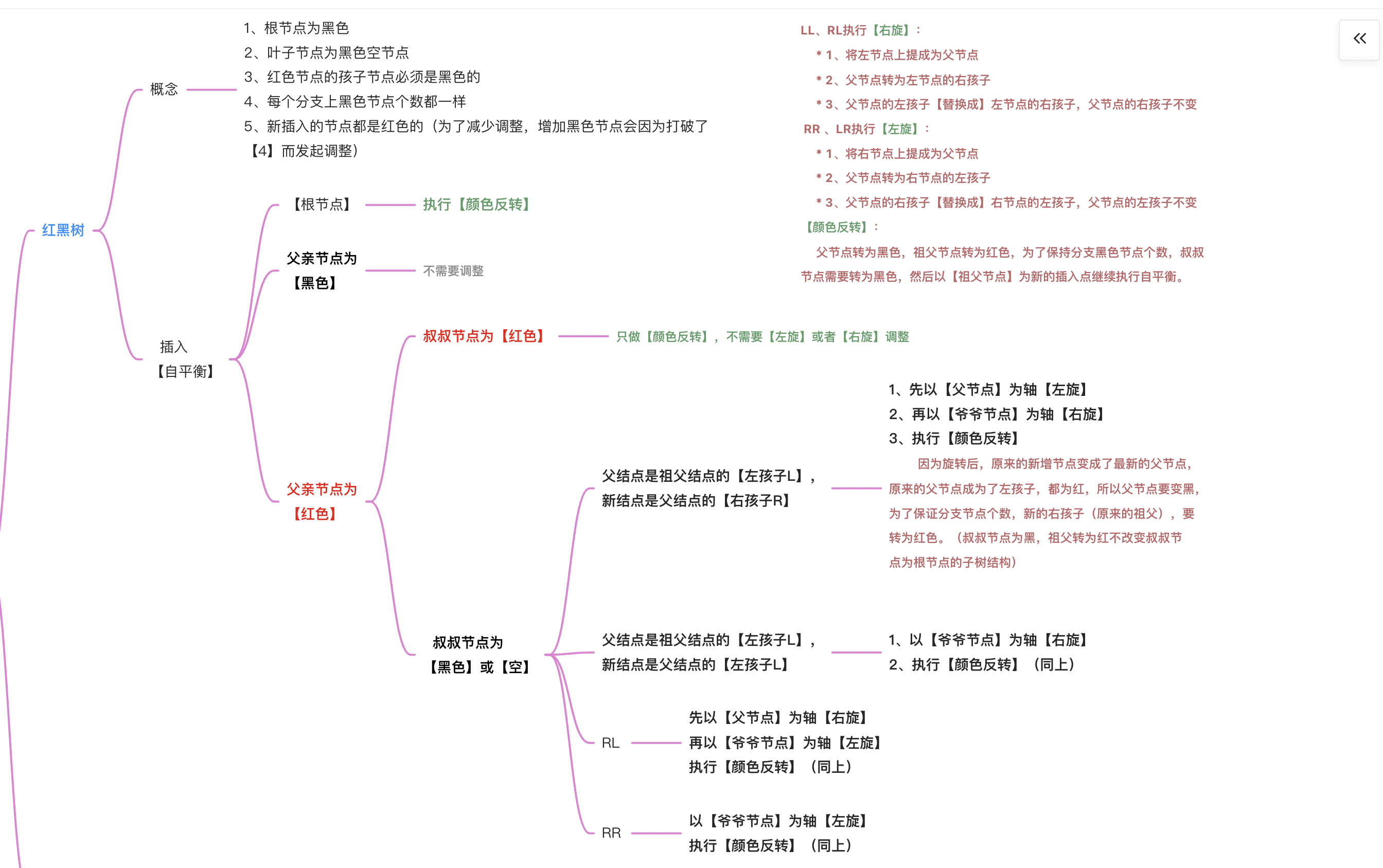
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
package tree.red.black;
 
 
/**
 * @author: tianhaichao
 * @date: 2022/8/29 14:27
 * @description: 1、根节点为黑色
 * 2、叶子节点为黑色空节点
 * 3、红色节点的孩子节点必须是黑色的
 * 4、每个分支上黑色节点个数都一样
 * 5、新插入的节点都是红色的（为了减少调整，增加黑色节点会因为打破了【4】而发起调整）
 */
public class RBTree {
    private static RBTreeNode root;
 
    /**
     * @author: tianhaichao
     * @date: 2022/9/20 15:55
     * @description: 红黑树插入节点，如果打破了红黑树的规则，需要自平衡做调整
     * 分以下几种情况：
     * 1、父亲节点为【黑色】  ————  插入红色节点后，没有打破红黑树的规则，【不需要做调整】
     * 2、父亲节点为【红色】  ————  插入节点为红色，需要做【颜色反转】，将父亲节点由红色变为黑色，为了不改变分支上black节点的个数，需要继而向上反转爷爷和祖先节点的颜色
     * a、叔叔节点为【红色】    -----  因为叔叔节点是红色，爷爷节点转变为红色后，叔叔节点必须要转变为黑色。在这个局部的子树中，两个分支上的black节点个数都没有变，所以【不需要左旋或右旋调整】。
     * b、叔叔节点为【黑色或空】 -----  因为叔叔节点是黑色，因为爷爷节点转而为红色，使得叔叔分支上的black节点少了一个，所以需要通过【自平衡】重新回到红黑树
     * （叶子结点也是黑色）
     * RL: 1、执行【颜色反转】2、先以【父节点】为轴【左旋】3、再以【爷爷节点】为轴【右旋】
     * RR: 1、执行【颜色反转】2、以【爷爷节点】为轴【右旋
     * LR: 1、执行【颜色反转】2、先以【父节点】为轴【右旋】3、再以【爷爷节点】为轴【左旋】
     * LL: 1、执行【颜色反转】2、以【爷爷节点】为轴【左旋】
     */
    public static void insert(int data) {
        RBTreeNode node = new RBTreeNode(data);
        if (root == null) {
            // 根节点是黑色的
            root = node;
            setBlack(node, true);
            return;
        } else {
            // 如果根节点不为空，循环找到叶子节点，执行树插入
            RBTreeNode parentNode = root;
            RBTreeNode sonNode = null;
            // 比较大小分边
            if (data >= parentNode.getData()) {
                // 遍历右边
                sonNode = parentNode.getRight();
            } else {
                // 遍历左边
                sonNode = parentNode.getLeft();
            }
 
            // 子节点不为空，继续遍历，直到找到叶子节点
            while (sonNode != null) {
                parentNode = sonNode;
                if (data >= parentNode.getData()) {
                    // 遍历右边
                    sonNode = parentNode.getRight();
                } else {
                    // 遍历左边
                    sonNode = parentNode.getLeft();
                }
            }
            // sonNode == null 是叶子节点
            if (data >= parentNode.getData()) {
                //插入右节点
                parentNode.setRight(node);
                node.setPrarent(parentNode);
                // 新建都是红色
                setBlack(node, false);
            } else {
                //插入左节点
                parentNode.setLeft(node);
                node.setPrarent(parentNode);
                // 新建都是红色
                setBlack(node, false);
            }
            // 执行自平衡平衡方法
            balanceInsert(node);
 
        }
    }
 
    public static void setBlack(RBTreeNode node, boolean isBlack) {
        if(node == null){
            return;
        }
        if (node != root) {
            node.setBlack(isBlack);
        } else {
            node.setBlack(true);
        }
    }
 
    /**
     * @author: tianhaichao
     * @date: 2022/9/20 17:38
     * @description:自平衡分以下几种情况： 1、父亲节点为【黑色】  ————  插入红色节点后，没有打破红黑树的规则，【不需要做调整】
     * 2、父亲节点为【红色】  ————  插入节点为红色，需要做【颜色反转】，将父亲节点由红色变为黑色，为了不改变分支上black节点的个数，需要继而向上反转爷爷和祖先节点的颜色
     * a、叔叔节点为【红色】    -----  因为叔叔节点是红色，爷爷节点转变为红色后，叔叔节点必须要转变为黑色。在这个局部的子树中，两个分支上的black节点个数都没有变，所以【不需要左旋或右旋调整】。
     * b、叔叔节点为【黑色或空】 -----  因为叔叔节点是黑色，因为爷爷节点转而为红色，使得叔叔分支上的black节点少了一个，所以需要通过【自平衡】重新回到红黑树
     * （叶子结点也是黑色）
     * RL: 1、执行【颜色反转】2、先以【父节点】为轴【左旋】3、再以【爷爷节点】为轴【右旋】
     * RR: 1、执行【颜色反转】2、以【爷爷节点】为轴【右旋
     * LR: 1、执行【颜色反转】2、先以【父节点】为轴【右旋】3、再以【爷爷节点】为轴【左旋】
     * LL: 1、执行【颜色反转】2、以【爷爷节点】为轴【左旋】
     */
    public static void balanceInsert(RBTreeNode node) {
        //判断father的颜色
        RBTreeNode farther = node.getPrarent();
        // 父节点是红色的，需要自平衡
        while (farther != root && farther != null && farther.isBlack() == false) {
            RBTreeNode grandFarther = farther.getPrarent();
            // 父亲节点是祖父的右孩子
            if (grandFarther.getRight() == farther) {
                // 判断叔叔节点颜色 —— red 【颜色反转】不需要【左旋】或【右旋】调整
                // 如果叔叔节点不为空，且为红色，反转叔叔节点颜色，祖父节点作为父节点向上传递
                if (grandFarther.getLeft() != null && grandFarther.getLeft().isBlack() == false) {
                    setBlack(farther, true);
                    setBlack(grandFarther, false);
                    setBlack(grandFarther.getLeft(), true);
                    // 此时的改变已经传递到了祖父，祖父变成了红色，相当于新插入
                    farther = grandFarther.getPrarent();
                    node= grandFarther;
                    continue;
                } else {
                    //叔叔节点为黑色或空
                    if(farther.getLeft()==node){
                        //RL 右旋 成为RR 然后 以祖父节点左旋
                        rightRotate(farther);
                    }
                    //RR
                    farther = leftRotate(grandFarther);
                    setBlack(farther, true);
                    setBlack(farther.getRight(), false);
                    setBlack(farther.getLeft(), false);
                    // 通过调整，father替代祖父的位置变成了黑色，所有分支黑色节点的个数没有变化，整棵树重新满足红黑树规则，跳出循环
                    break;
                }
 
            }
            // 父亲节点是祖父的左孩子
            if (grandFarther.getLeft() == farther) {
                // 判断叔叔节点颜色 —— red 【颜色反转】不需要【左旋】或【右旋】调整
                // 如果叔叔节点不为空，且为红色，反转叔叔节点颜色，祖父节点作为父节点向上传递
                if (grandFarther.getRight() != null && grandFarther.getRight().isBlack() == false) {
                    setBlack(farther, true);
                    setBlack(grandFarther, false);
                    setBlack(grandFarther.getRight(), true);
                    // 此时的改变已经传递到了祖父，祖父变成了红色，相当于新插入
                    farther = grandFarther.getPrarent();
                    node= grandFarther;
                    continue;
                } else {
                    //叔叔节点为黑色或空
                    if(farther.getRight()==node){
                        //LR 左旋 成为LL 然后 以祖父节点右旋
                        farther = leftRotate(farther);
                    }
                    //LL
                    farther = rightRotate(grandFarther);
                    setBlack(farther, true);
                    setBlack(farther.getRight(), false);
                    setBlack(farther.getLeft(), false);
                }
            }
 
        }
 
    }
 
    /**
     * @author: tianhaichao
     * @date: 2022/8/30 14:44
     * @description: node 旋转节点 RR 、LR执行左旋
     * 1、将右节点上提成为父节点
     * 2、父节点转为右节点的左孩子
     * 3、父节点的右孩子【替换成】右节点的左孩子，父节点的左孩子不变
     * return 旋转完后的父节点，也就是右孩子【将右节点上提成为父节点】
     */
    public static RBTreeNode leftRotate(RBTreeNode node) {
        RBTreeNode right = node.getRight();
        RBTreeNode father = node;
        // 如果右节点存在左孩子,父节点的右孩子【替换成】右节点的左孩子
        father.setRight(right.getLeft());
        // 将右节点上提成为父节点 变成祖父的孩子
        if (father.getPrarent() == null || father == root) {
            root = right;
        } else if (father.getPrarent().getLeft() == father) {
            father.getPrarent().setLeft(right);
        } else {
            // 如果旋转节点是父节点的右节点
            father.getPrarent().setRight(right);
        }
        right.setPrarent(father.getPrarent());
//        父节点转为右节点的左孩子
        right.setLeft(father);
        father.setPrarent(right);
        return right;
    }
 
    /**
     * @return 旋转之后的父节点，也就是左孩子【将左节点上提成为父节点】
     * @author: tianhaichao
     * @date: 2022/9/20 18:31
     * @description: LL或RL执行右旋
     * 执行右旋，
     * 1、将左节点上提成为父节点
     * 2、父节点转为左节点的右孩子
     * 3、父节点的左孩子【替换成】左节点的右孩子，父节点的右孩子不变
     */
    public static RBTreeNode rightRotate(RBTreeNode node) {
        RBTreeNode left = node.getLeft();
        RBTreeNode father = node;
        // 父节点的左孩子【替换成】左节点的右孩子，父节点的右孩子不变
        father.setLeft(left.getRight());
        //将左节点上提成为父节点
        if (father.getPrarent() == null || father == root) {
            root = left;
        } else if (father.getPrarent().getRight() == father) {
 
            father.getPrarent().setRight(left);
        } else {
            father.getPrarent().setLeft(left);
        }
        left.setPrarent(father.getPrarent());
        // 父节点转为左节点的右孩子
        father.setPrarent(left);
        left.setRight(father);
        return left;
    }
 
    public static void main(String[] args) {
        int[] array = new int[]{10, 3, 5, 2, 5, 6, 4, 12, 15, 16, 17, 18};
        for (int i : array) {
            RBTree.insert(i);
            preTraversal(root);
            System.out.println("----" + i);
        }
        System.out.println("==========================");
        //排序输出
        midTraversal(root);
    }
 
    /**
     * @author: tianhaichao
     * @date: 2022/9/20 15:10
     * @description:中序遍历
     */
    public static void midTraversal(RBTreeNode node) {
        if (node == null) {
            return;
        }
        midTraversal(node.getLeft());
        System.out.print(node.getData() +"  ");
        midTraversal(node.getRight());
    }
    /**
     * @author: tianhaichao
     * @date: 2022/9/20 15:10
     * @description:中序遍历
     */
    public static void preTraversal(RBTreeNode node) {
        if (node == null) {
            return;
        }
        int left = node.getLeft()!=null?node.getLeft().getData():0;
        int right = node.getRight() != null?node.getRight().getData():0;
        System.out.print(node.getData() +"【"+node.isBlack()+left+"  "+right+"】"+ "  ");
        preTraversal(node.getLeft());
        preTraversal(node.getRight());
    }
}
 
 
package tree.red.black;
 
/**
 * @author: tianhaichao
 * @date: 2022/8/29 14:20
 * @description: 红黑树节点
 */
public class RBTreeNode {
    private int data;
    private RBTreeNode prarent;
    private RBTreeNode left;
    private RBTreeNode right;
// get set方法省略……
}