matlab练习程序（线性常微分方程组矩阵解）

之前有通过ode和simulink解线性常微分方程组。

除了上面两种方法，线性常微分方程组还可以通过矩阵的方法求解。

比如下面这个之前使用的方程组：

x'' = x' - x + y' -z'

y'' = y' - y - x'

z'' = z' - z + x'

可以写成下面矩阵形式：

 

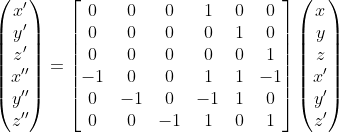
设这个矩阵为A，那么解可以表示为如下形式：

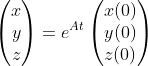
可以直接通过matlab的expm函数求解。

或者对A做特征值分解[e,v]=eig(A)，然后得到特征值的exp对角阵，最后通过欧拉公式求解。

matlab代码如下：

clear all;close all;clc;
X0=[3;1;-1;1;0.5;0];

fvdp = @(T,Y) [Y(4);        %x'
    Y(5);                   %y'
    Y(6);                   %z'
    Y(4)-Y(1)+Y(5)-Y(6);    %x''
    Y(5)-Y(2)-Y(4);         %y''
    Y(6)-Y(3)+Y(4)];        %z'']

[T,Y] = ode45(fvdp, [0:0.1:5],X0);

for i=1:6
    plot(T,Y(:,i),'r-o');
    hold on;
end

A = [0 0 0 1 0 0;
    0 0 0 0 1 0;
    0 0 0 0 0 1;
    -1 0 0 1 1 -1;
    0 -1 0 -1 1 0;
    0 0 -1 1 0 1];

[e,v] = eig(A);

re=[];
for t = 0:0.1:5

    M = e*(exp(real(v)*t).*(cos(imag(v)*t)+1i*sin(imag(v)*t)))*inv(e);
    %M = e*expm(v*t)*inv(e);
    %M = expm(A*t);
    Y = M*X0;

    re=[re;Y'];
end

Y = re-re(1,:);

for i=1:6
    plot(T,real(Y(:,i))+X0(i),'b*');
end
grid on;

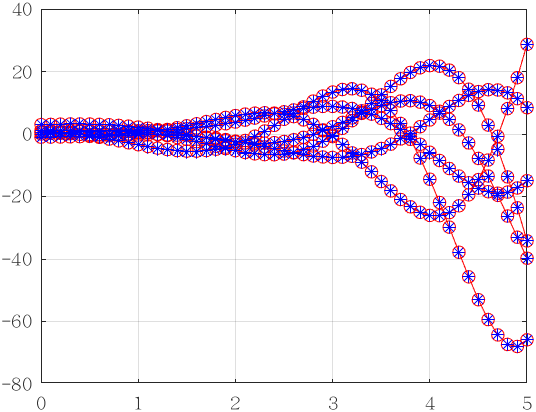
结果和ode解法是一致的：