matlab练习程序（LQR路径跟踪）

LQR 是一种优化控制方法，设计目标是找到一组控制输入，使得线性系统的状态轨迹尽可能地接近目标，同时使控制输入尽可能小。其目标函数是一个二次型成本函数。

分为以下几个步骤：

1. 设系统动态方程为：

其中x为状态量，u为控制输入，A和B为状态转移和控制矩阵。

2. 定义一个性能指标，即控制器的优化目标。在LQR中，通常采用二次型性能指标，即系统状态和控制输入的加权和的二次型。这个性能指标可以包括状态的偏差、控制输入的幅值等，可以根据具体需求进行调整：

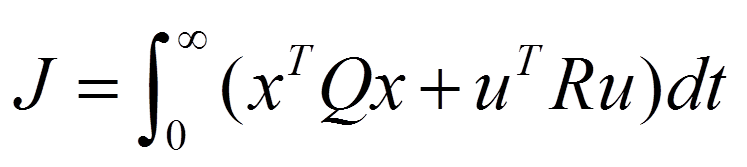
其中，Q和R是权重矩阵，用于调整状态偏差和控制输入的相对重要性。

3. 设计LQR控制器，通过解离散时间的Riccati方程，可以获得最优的状态反馈控制器。这个控制器以状态为输入，根据系统的状态信息来生成控制输入，以最小化性能指标。

方程如下：

 

解该方程可以参考之前的文章。

4. 最后得到最优控制器公式如下：

 

其中K为状态反馈矩阵，根据当前系统状态可以得到最终控制量u=-Kx。

matlab代码如下：

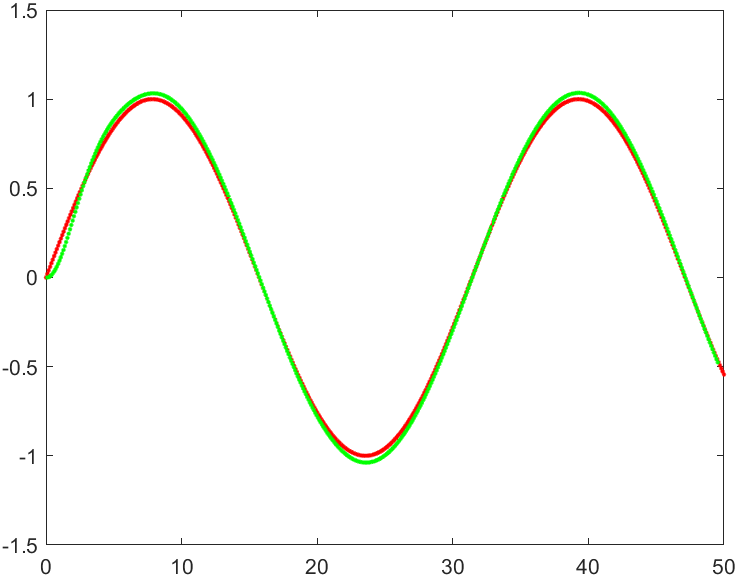
clear all;close all;clc;

v =1;
lambda = 2;
dt = 0.1;
L=2.5;

x = 0:0.1:50;
y = sin(x/5);
path = [x' y'];
for i=2:length(path)
    dx = path(i,1)-path(i-1,1);
    dy = path(i,2)-path(i-1,2);
    path(i-1,3) = atan2(dy,dx);
end
path(length(path),3) = path(length(path)-1,3);
plot(path(:,1),path(:,2),'r.');
hold on;

curp=[0 0 0];

for i=1:length(path)
    
    d = path(:,1:2) - curp(1:2);
    dis = d(:,1).^2 + d(:,2).^2;
    [~,ind] = min(dis);                                     %找路径最近点索引

    dx = curp(1) - path(ind,1);
    dy = curp(2) - path(ind,2);
    dyaw = curp(3) - path(ind,3);  
    xstate = [dx;dy;sin(dyaw)];                                  %状态变量
        
    Ad=[1    0   -v*sin(path(ind,3))*dt;
        0    1   v*cos(path(ind,3))*dt;
        0    0    1];                                      %线性离散后的系统矩阵
    
    Bd=[cos(path(ind,3))*dt     0;
        sin(path(ind,3))*dt     0;
        0 dt];         %线性离散后的控制矩阵
  
    Q = [10 0 0;
        0 10 0;
        0 0 1];     %初始化LQR的权重矩阵
    R =[1 0;
        0 1];       %初始化LQR的权重矩阵
    
    %*********黎卡提方程求解**********%  
    PN =Q;
    err =1e-5;     
    error = 1;
    k=1;
    while(error>err)
        PN_1 = Q + Ad'*PN*Ad - Ad'*PN*Bd*inv(R+Bd'*PN*Bd)*(Bd'*PN*Ad);
        error = norm(PN-PN_1);
        PN = PN_1;
        k = k+1;
        if k>400 
            break;
        end
    end
    P =PN_1;
    K = (R+Bd'*P*Bd)\Bd'*P*Ad;                                  %计算状态反馈增益K
    %***************************************%
    
    U  = - K * xstate;                                          %线性反馈控制量
    deltav = U(1);
    deltastr = U(2);
    
    curp(1) = curp(1) + dt*v*cos(curp(3));
    curp(2) = curp(2) + dt*v*sin(curp(3));
    curp(3) = curp(3) + dt*v*tan(deltastr)/L;
    
    plot(curp(1),curp(2),'g.');
end
%axis equal;

结果如下：