matlab练习程序(Schur补)
Schur 补是一种矩阵分解方法,通过将一个大的矩阵分解为几个较小的矩阵来简化计算,通常能够提高矩阵求逆的速度。
对于形如下面的矩阵:
可以把矩阵划分为左上、右上、左下、右下四个分块矩阵。
得到矩阵:
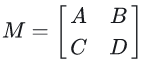
根据A和D的奇异性,可以分两种情况。
如果A可逆,则有:
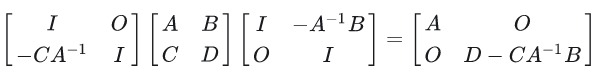
如果D可逆,则有:
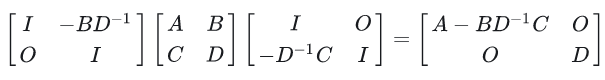
公式两边同时求逆,得到下面两组公式:
如果A可逆,则有:
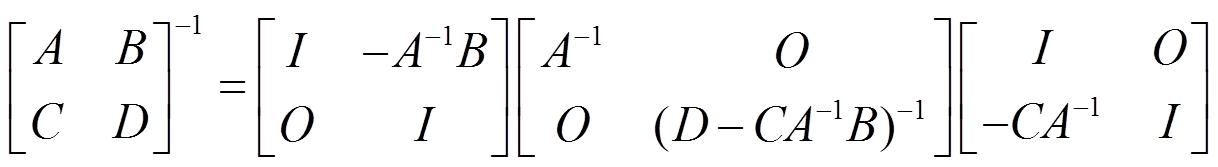
如果D可逆,则有:
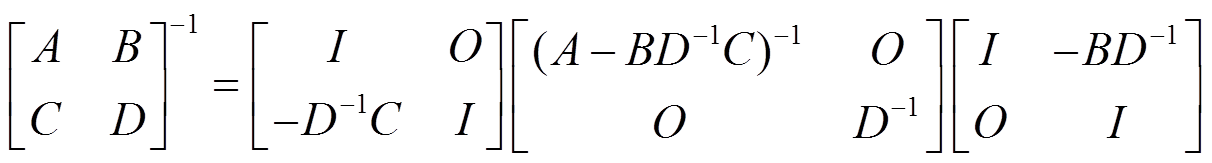
根据上述公式,就能求出原始矩阵的逆。
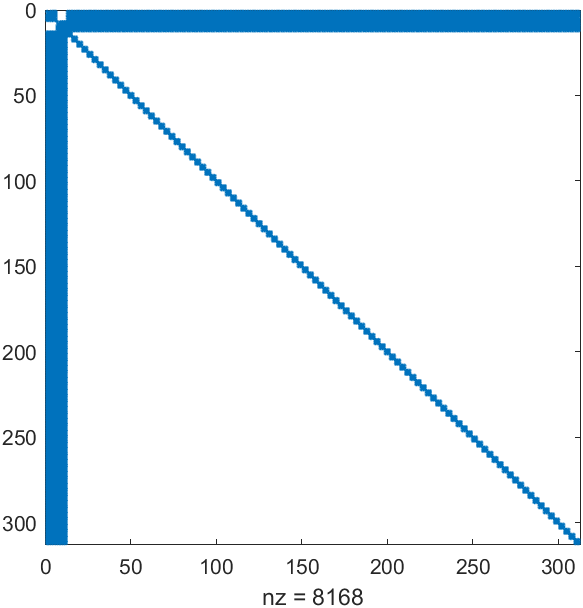
下面的矩阵就是之前介绍BA中的H矩阵,当时直接inv求逆了,这里用Schur补求逆。
matlab代码如下:
clear all;close all;clc; load H.mat spy(H); n = length(H); m = 12; A = H(1:m,1:m); B = H(1:m,m+1:end); C = H(m+1:end,1:m); D = H(m+1:end,m+1:end); if det(A)~=0 A_inv = inv(A); U = [eye(m) -A_inv*B;zeros(n-m,m) eye(n-m)]; V = [A_inv zeros(m,n-m);zeros(n-m,m) inv(D-C*A_inv*B)]; W = [eye(m) zeros(m,n-m);-C*A_inv eye(n-m)]; H_inv= U*V*W; else D_inv = inv(D); U = [eye(m) zeros(m,n-m);-D_inv*C eye(n-m)]; V = [inv(A-B*D_inv*C) zeros(m,n-m);zeros(n-m,m) inv(D)]; W = [eye(m) -B*D_inv; zeros(n-m,m) eye(n-m)]; H_inv= U*V*W; end dif = inv(H) - H_inv; sum(dif(:))



