matlab练习程序(DLT)
在计算位姿的时候,一般我们有一些观测量,这些观测量有些是三维的、有些是二维的,因此需要用到不同的方法。
如果是3D-3D的位姿计算,一般可以用这几种方法(【1】,【2】,【3】,【4】)。
如果是3D-2D的位姿计算,一般可以用PnP-BA或者是本篇的DLT(直接线性变换)方法。
如果是2D-2D的位姿计算,一般可以用对极几何的方法,不过算不出尺度。
三维点投影到归一化二维平面可以用下面公式表示:
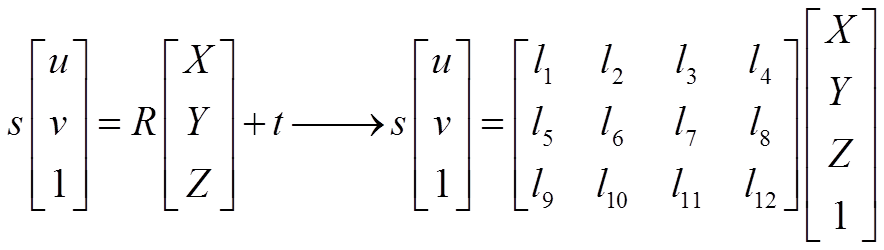
其中uv是二维归一化平面点,XYZ是三维投影点。
整理后可得AX=0这种形式,X就是公式中的12个l,A矩阵形式如下:

对于AX=0这种问题,一般都是对A奇异值分解或者对A'A特征值分解,然后拿其最小特征值对应的特征向量,作为该问题的解。
matlab代码如下:
clear all;close all;clc; p = [rand(100,3)*100 ones(100,1)]'; i=1.2*pi/180.0; j=88*pi/180.0; k=-5.1*pi/180.0; Rx=[1 0 0;0 cos(i) -sin(i); 0 sin(i) cos(i)]; Ry=[cos(j) 0 sin(j);0 1 0;-sin(j) 0 cos(j)]; Rz=[cos(k) -sin(k) 0;sin(k) cos(k) 0;0 0 1]; R=Rz*Ry*Rx; T = [200;40;50]; srcR = [R T;0 0 0 1] newp = inv(srcR)*p; uv =[newp(1,:)./newp(3,:); newp(2,:)./newp(3,:)]; xyz = p(1:3,:)'; [newR, err] = DLTcalib(xyz, uv') function [Tr, x] = Normalization(nd, x) [m, s] = deal(mean(x, 1), std(x)); if nd == 2 Tr = [s(1), 0, m(1); 0, s(2), m(2); 0, 0, 1]; else Tr = [s(1), 0, 0, m(1); 0, s(2), 0, m(2); 0, 0, s(3), m(3); 0, 0, 0, 1]; end Tr = inv(Tr); x = (Tr * [x'; ones(1, size(x, 1))]).'; x = x(:, 1:nd); end function [H, err] = DLTcalib(xyz, uv) n = size(xyz, 1); [Txyz, xyzn] = Normalization(3, xyz); [Tuv, uvn] = Normalization(2, uv); A = zeros(2*n, 12); for i = 1:n x = xyzn(i, 1); y = xyzn(i, 2); z = xyzn(i, 3); u = uvn(i, 1); v = uvn(i, 2); A(2*i-1, :) = [x, y, z, 1, 0, 0, 0, 0, -u*x, -u*y, -u*z, -u]; A(2*i, :) = [0, 0, 0, 0, x, y, z, 1, -v*x, -v*y, -v*z, -v]; end [~, ~, V] = svd(A); % Camera projection matrix H = reshape(V(:,end), [4, 3])'; % Denormalization H = pinv(Tuv) * H * Txyz; H = inv([H;0 0 0 1]); H(1:3,1:3) = H(1:3,1:3)./norm(H(1:3,1:3)); uv2 = (inv(H) * [xyz'; ones(1, n)])'; uv2 = uv2(:, 1:2) ./ uv2(:, 3); % Mean distance: err = sqrt(mean(sum((uv2 - uv).^2, 2))); end
可以看出计算得到的位姿和最初设置的位姿是一样的。
不过该方法计算时没有考虑旋转矩阵的约束,即A'A=I这种条件,因此计算的到的旋转量可能会有问题。
PnP-BA这种方法是不存在这种问题的。







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」
· 写一个简单的SQL生成工具
2015-12-02 Boost练习程序(multi_index_container)
2015-12-02 mathematica练习程序(图像取反)
2011-12-02 矩阵的LU分解 c++