matlab练习程序（PnP-BA）

通过3D-2D匹配点计算位姿，除了用上篇的DLT来求解，还可以用非线性优化方式求解。

这篇就用BA的方法求解PnP问题。

使用非线性优化通常要先确定下面四个要素：

1. 待优化模型，模型和上一篇是一样的，三维点通过旋转平移矩阵变换到像空间，然后通过内参投影到二维像平面上，可以用下面几个方程表示：

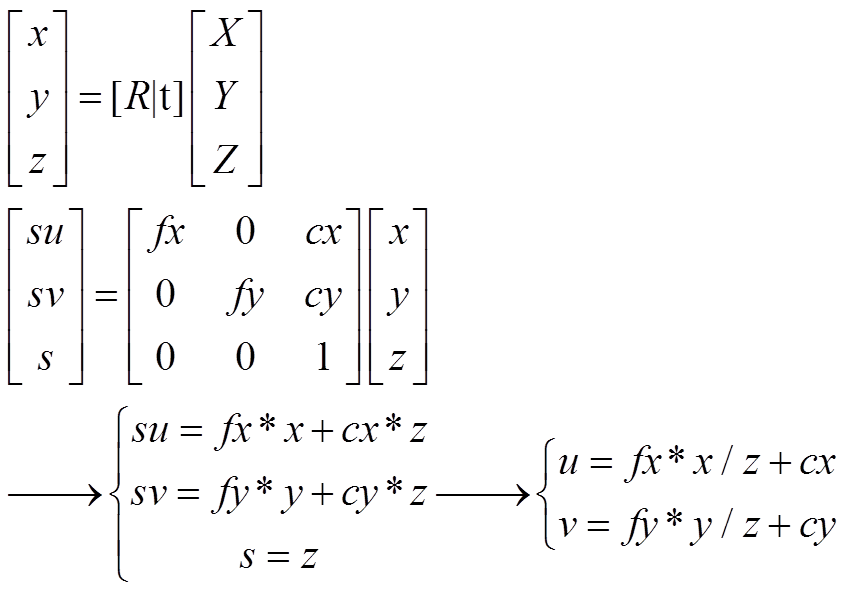
其中XYZ为三维空间点；Rt为相机位姿，也是待求参数；xyz为像空间点；fx,fy,cx,cy为内参；uv为像平面点。

2. 待优化参数，这里就是待求位姿了Rt了，由于使用了李代数并且只有一个相机，因此一共6个参数。

3. 残差，三维点通过模型投影到像平面上的二维点和检测到的二维特征点的差值。

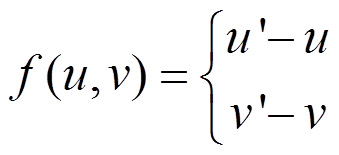
其中f就是残差，u'v'为检测到的二维特征点，uv为通过模型投影到二维像平面上的点。

4. 雅克比矩阵。

雅克比矩阵就是对f求Rt的偏导数，不过这里用到了李代数，因此推导不是很简单。

基本思想就是uv首先对xyz求导，然后xyz再对Rt求导，Rt作为李群，其切平面用李代数表示，然后就可以用李代数表示这个导数了，后一步用到的方法在这篇文章中有实践。

公式如下：

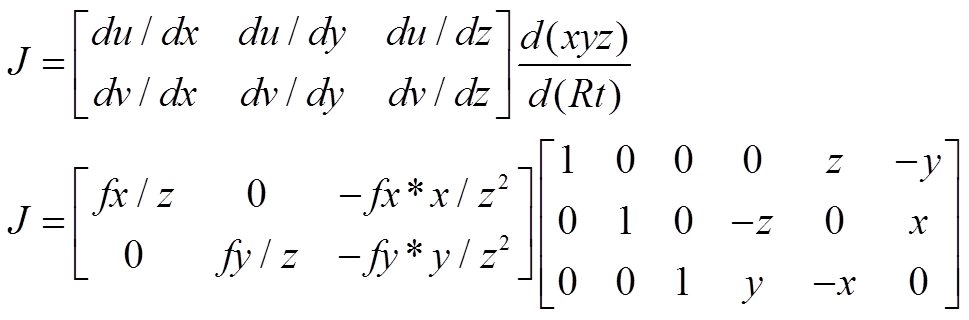
d(xyz)/d(Rt)这里是一个我简化的示意形式，表示Rt的李代数。

上面四个要素都集齐后就可以做BA优化迭代求解位姿了。

下面代码中为了简便，没有考虑内参，用的归一化像平面，其实残差中的fxfy和雅克比中的fxfy在后面的运算中是能够消掉的。

matlab程序如下：

clear all;close all;clc;

p = [rand(100,3)*100 ones(100,1)]';

i=1.2*pi/180.0;
j=88*pi/180.0;
k=-2.1*pi/180.0;
Rx=[1 0 0;0 cos(i) -sin(i); 0 sin(i) cos(i)];
Ry=[cos(j) 0 sin(j);0 1 0;-sin(j) 0 cos(j)];
Rz=[cos(k) -sin(k) 0;sin(k) cos(k) 0;0 0 1];
R=Rz*Ry*Rx;
T = [200;40;50];
srcR = [R T;0 0 0 1]

newp = inv(srcR)*p;
uv =[newp(1,:)./newp(3,:) ; newp(2,:)./newp(3,:)];

initR = [R+rand(3,3)*0.1 T+10*rand(3,1);0 0 0 1]
x = SE3_to_se3(inv(initR));

for i=1:30  
    J = calcJab(x,p);
    fx = calcCost(x,p,uv);    
    dx = inv(J'*J)*J'*fx;
    % x = x + dx';
    x = SE3_to_se3(se3_to_SE3(dx')*se3_to_SE3(x));   
end
inv(se3_to_SE3(x))

function J = calcJab(x,p)
R = se3_to_SE3(x);
new_P = R * p;

num = size(p,2);
J = zeros(2*num,6);
for i=1:num
    
    X = new_P(1,i);
    Y = new_P(2,i);
    Z = new_P(3,i);
    
    Jabep = [1/Z 0 -X/(Z*Z);0 1/Z -Y/(Z*Z)];
    Jab = zeros(3,6);
    Jab(1:3,1:3) = eye(3,3);
    Jab(1:3,4:6) = -[0 -Z Y;Z 0 -X;-Y X 0];
    
    J((i-1)*2+1:i*2,:) = Jabep*Jab;
end
end

function fx = calcCost(x,p,uv)
R = se3_to_SE3(x);
new_P = R * p;

num = size(p,2);
fx = zeros(2*num,1);
for i=1:num
    
    u = uv(1,i);
    v = uv(2,i);
    
    X = new_P(1,i) / new_P(3,i);
    Y = new_P(2,i) / new_P(3,i);
    
    fx((i-1)*2+1:i*2) = [u - X;v - Y];
end
end

function se3 = SE3_to_se3( SE3 )
% UNTITLED Summary of this function goes here
% Detailed explanation goes here

R=SE3(1:3,1:3);
theta=acos((trace(R)-1)/2);
lnR=(theta/(2*sin(theta)))*(R-R');
w=[-lnR(2,3) lnR(1,3) -lnR(1,2)];
wx=[0 -w(3) w(2);w(3) 0 -w(1);-w(2) w(1) 0];
if(theta==0)
    Vin=eye(3);
else
    A=sin(theta)/theta;
    B=(1-cos(theta))/(theta^2);
    Vin=eye(3)-(1/2)*wx+(1/(theta^2))*(1-(A/(2*B)))*(wx*wx);
end
u=Vin*SE3(1:3,4);
se3=[u' w];
end

function SE3 = se3_to_SE3( se3 )
% se3_SE3 Exponential Mapping from Lie Algebra to Lie Group
% se3 is a 1x6 Column Vector of the form=[v1 v2 v3 w1 w2 w3] which is
% defined using 6 Generator Matrices(4x4)
% each of the six elements on multiplication with the generator matrices
% as follows give the complete matrix:
% se3 = v1*G1 + v2*G2 + v3*G3 + w1*G4 + w2*G5 + w3*G6
% To map se3 to SE3 we need to perform e^(se3)
% This can be done by following the algorithm:
% Algorithm

w=se3(4:6)';
u=se3(1:3)';
wx=[0 -w(3) w(2);w(3) 0 -w(1);-w(2) w(1) 0];
theta=sqrt(w'*w);
if(theta~=0)
    A=sin(theta)/theta;
    B=(1-cos(theta))/(theta^2);
    C=(1-A)/(theta^2);
else
    A=0;
    B=0;
    C=0;
end
R=eye(3)+(A*wx)+(B*(wx*wx));
V=eye(3)+B*wx+C*(wx*wx);
Vp=V*u;
SE3=zeros(4);
SE3(1:3,1:3)=R;
SE3(1:3,4)=Vp;
SE3(4,4)=1;
end

这种方法计算出来的R是符合旋转矩阵定义的，不会出现DLT可能出现的求解出的矩阵不符合定义的情况。