matlab练习程序（Bundle Adjustment）

BA作为视觉SLAM中后端优化的一个核心点还是比较重要的。

BA根据优化量的不同可以分为三种形式。

Full BA：观测点和位姿同时优化，一般是视觉SLAM后端的核心。

Motion BA：已知观测点，优化位姿，一般用来定位。之前的文章中有用到BA单做位姿计算的方法。

Struct BA：已知位姿，优化观测点，一般用来建图。

不论是哪种BA方法，一般模型和残差都是一样的，不一样的都是待优化参数和雅克比矩阵。

下面优化同样用到了李群李代数的方法，雅克比矩阵参考了之前的两篇文章([1]，[2])。

下面代码流程大致分三步：

1. 设置100个随机三维点，再设置两组位姿。 然后对位姿和随机点加上一些扰动，送入循环。

2. 确定优化四大步：模型，残差，待优化参数和雅克比矩阵。

3. 迭代优化出结果。

matlab代码如下：

clear all;close all;clc;
warning off;

p = [rand(100,3)*100 ones(100,1)]';

R = rot(0,90,0);
R1 = rot(-0.5,89.4,-1.0);
R2 = rot(0.5,90.5,1);
T = [200;40;50];

pos1 = [R1 T+5*rand(3,1);0 0 0 1]
pos2 = [R2 T+5*rand(3,1);0 0 0 1]

newp1 = inv(pos1)*p;
newp2 = inv(pos2)*p;

uv1 =[newp1(1,:)./newp1(3,:) ; newp1(2,:)./newp1(3,:)];
uv2 =[newp2(1,:)./newp2(3,:) ; newp2(2,:)./newp2(3,:)];

initPos = [R T;0 0 0 1]

x = zeros(2*6+3*100,1);
x(1:6) = SE3_to_se3(inv(initPos))';
x(7:12) = SE3_to_se3(inv(initPos))';
x(13:end) = reshape(p(1:3,:),[300,1]) + rand(300,1);

for i=1:100
    
    J = calcJab(x);
    fx = calcCost(x,uv1,uv2);
    
    % norm(fx)
    H = J'*J;
    dx = inv(H + 0.01*eye(size(H)))*J'*fx;
    
    x1 = SE3_to_se3(se3_to_SE3(dx(1:6)')*se3_to_SE3(x(1:6)'));
    x2 = SE3_to_se3(se3_to_SE3(dx(7:12)')*se3_to_SE3(x(7:12)'));
    x = x + dx;
    x(1:6) = x1';
    x(7:12) = x2';
    
end

norm(fx)

%show result
plot(uv1(1,:),uv1(2,:),'ro');
hold on;
plot(uv2(1,:),uv2(2,:),'go');

pos1 = se3_to_SE3(x(1:6)');
pos2 = se3_to_SE3(x(7:12)');

P = [reshape(x(13:end),[3,100]);ones(1,100)];

p1 = pos1 * P;
p2 = pos2 * P;

uv1 =[p1(1,:)./p1(3,:) ; p1(2,:)./p1(3,:)];
uv2 =[p2(1,:)./p2(3,:) ; p2(2,:)./p2(3,:)];

plot(uv1(1,:),uv1(2,:),'r*');
hold on;
plot(uv2(1,:),uv2(2,:),'g*');

inv(pos1)
inv(pos2)
figure;
spy(H)

function J = calcJab(x)

newP = x(13:end);
newP = reshape(newP,[3,100]);
newP = [newP;ones(1,100)];

pos1 = se3_to_SE3(x(1:6)');
pos2 = se3_to_SE3(x(7:12)');
P1 = pos1 * newP;
P2 = pos2 * newP;

J = zeros(400,6*2+100*3);
for i=1:100
    X = P1(1,i);
    Y = P1(2,i);
    Z = P1(3,i);
    
    Jabep = [1/Z 0 -X/(Z*Z);0 1/Z -Y/(Z*Z)];
    Jab = zeros(3,6);
    Jab(1:3,1:3) = eye(3,3);
    Jab(1:3,4:6) = -[0 -Z Y;Z 0 -X;-Y X 0];
    
    J((i-1)*2+1:i*2,1:6) = Jabep*Jab;
    J((i-1)*2+1:i*2,12+(i-1)*3+1:12+i*3) = Jabep*pos1(1:3,1:3);
end

for i=1:100
    X = P2(1,i);
    Y = P2(2,i);
    Z = P2(3,i);
    
    Jabep = [1/Z 0 -X/(Z*Z);0 1/Z -Y/(Z*Z)];
    Jab = zeros(3,6);
    Jab(1:3,1:3) = eye(3,3);
    Jab(1:3,4:6) = -[0 -Z Y;Z 0 -X;-Y X 0];
    
    J(200+(i-1)*2+1:200+i*2,7:12) = Jabep*Jab;
    J(200+(i-1)*2+1:200+i*2,12+(i-1)*3+1:12+i*3) = Jabep*pos2(1:3,1:3);
end

end

function fx = calcCost(x,uv1,uv2)

newP = x(13:end);
newP = reshape(newP,[3,100]);
newP = [newP;ones(1,100)];

pos1 = se3_to_SE3(x(1:6)');
pos2 = se3_to_SE3(x(7:12)');
P1 = pos1 * newP;
P2 = pos2 * newP;

fx = zeros(400,1);
for i=1:100
    X = P1(1,i);
    Y = P1(2,i);
    Z = P1(3,i);
    u = uv1(1,i);
    v = uv1(2,i);
    fx((i-1)*2+1:i*2) = [u - X/Z;v - Y/Z];
end

for i=1:100
    X = P2(1,i);
    Y = P2(2,i);
    Z = P2(3,i);
    u = uv2(1,i);
    v = uv2(2,i);
    fx(200+(i-1)*2+1:200+i*2) = [u - X/Z;v - Y/Z];
end

end

function R=rot(i,j,k)
Rx=[1 0 0;0 cos(i) -sin(i); 0 sin(i) cos(i)];
Ry=[cos(j) 0 sin(j);0 1 0;-sin(j) 0 cos(j)];
Rz=[cos(k) -sin(k) 0;sin(k) cos(k) 0;0 0 1];
R=Rz*Ry*Rx;
end

function se3 = SE3_to_se3( SE3 )

R=SE3(1:3,1:3);
theta=acos((trace(R)-1)/2);
lnR=(theta/(2*sin(theta)))*(R-R');
w=[-lnR(2,3) lnR(1,3) -lnR(1,2)];
wx=[0 -w(3) w(2);w(3) 0 -w(1);-w(2) w(1) 0];
if(theta==0)
    Vin=eye(3);
else
    A=sin(theta)/theta;
    B=(1-cos(theta))/(theta^2);
    Vin=eye(3)-(1/2)*wx+(1/(theta^2))*(1-(A/(2*B)))*(wx*wx);
end
u=Vin*SE3(1:3,4);
se3=[u' w];
end

function SE3 = se3_to_SE3( se3 )

w=se3(4:6)';
u=se3(1:3)';
wx=[0 -w(3) w(2);w(3) 0 -w(1);-w(2) w(1) 0];
theta=sqrt(w'*w);
if(theta~=0)
    A=sin(theta)/theta;
    B=(1-cos(theta))/(theta^2);
    C=(1-A)/(theta^2);
else
    A=0;
    B=0;
    C=0;
end
R=eye(3)+(A*wx)+(B*(wx*wx));
V=eye(3)+B*wx+C*(wx*wx);
Vp=V*u;
SE3=zeros(4);
SE3(1:3,1:3)=R;
SE3(1:3,4)=Vp;
SE3(4,4)=1;
end

结果如下：

经典的箭头矩阵：

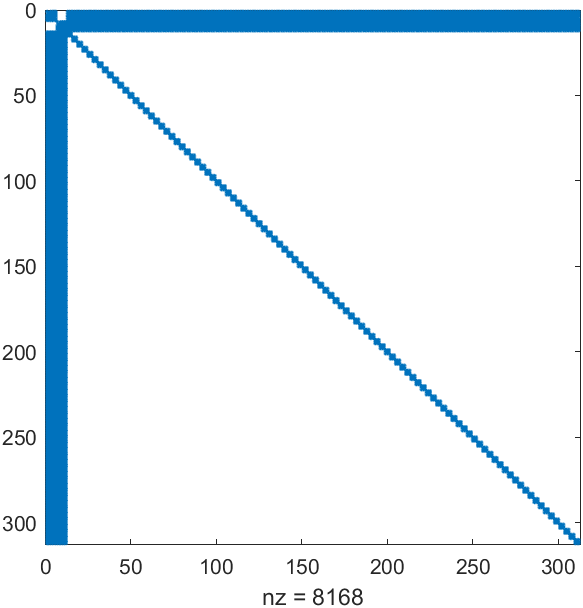
用优化后位姿将优化后的点云反投影到归一化图像坐标系结果：

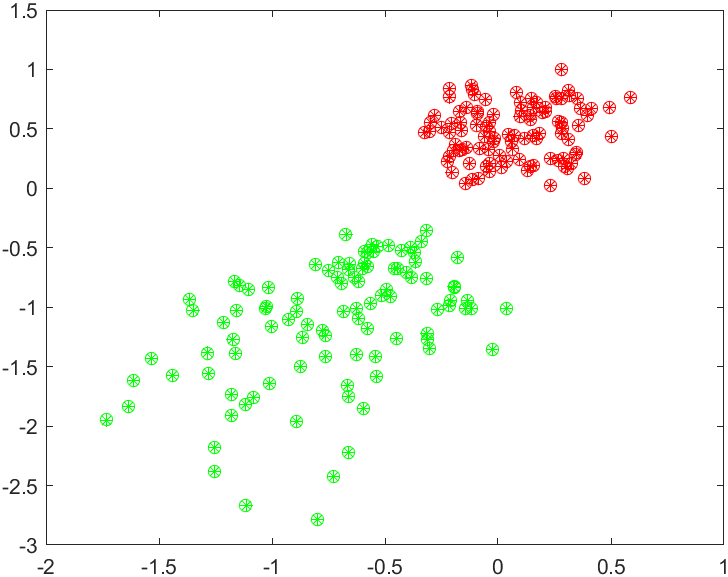
圈圈是真值，星星是结果。