matlab练习程序(无迹变换)
当数据通过非线性函数后,分布不再是高斯分布时,可以用无迹变换估计新数据的均值与方差。
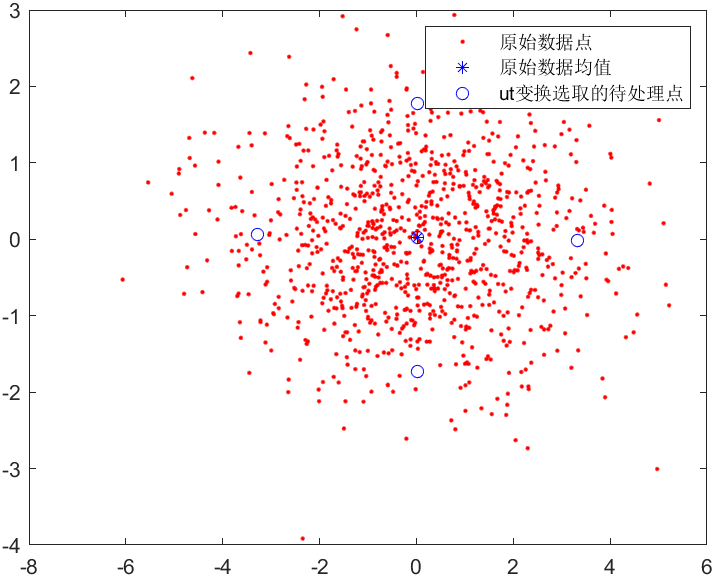
算法原理就是在原始数据均值周围根据方差选取一些待使用点,然后将这些点通过非线性函数,再通过加权平均的方式求出新分布的均值与方差。
如果我们选取的点非常多,并且将这些点都通过非线性函数,再估计均值与方差,那么就是粒子滤波了。
无迹变换的典型算法就是无迹卡尔曼滤波了,我这里只是单纯实验了无迹变换,没有涉及卡尔曼滤波部分,后面有时间应该会写无迹卡尔曼滤波。
无迹变换中选取加权的权重公式我看还挺复杂,并且我不是完全清楚其意义,所以这里直接暴力取权重了,对于实验数据效果还可以。
matlab代码如下:
clear all;close all;clc; % 非线性函数: % xpar = x+y % ypar = 5*x*x +y*y x = randn(1000,1)*2; y = randn(1000,1); mu = [mean(x);mean(y)]; P = [x y]'*[x y] / length(x); plot(x,y,'r.') hold on; plot(mu(1),mu(2),'b*') %%%%%%%%%%%%ut变换%%%%%%%%%%%%%%%%%%%% n = 2; N = 2*n+1; Wm = ones(1, N) * 1/(2*(n+1)); %这里比较暴力直接取权重 Wc = [Wm(1), Wm(2:end)+ones(1, 2*n)*1/(2*(n+1))]; %{ alpha = 0.9; %根据公式算权重,需要仔细考虑各个系数 kappa = 2; beta = 2; lambda = alpha^2 * (n + kappa) - n; Wm = zeros(1,2*n+1); Wc = zeros(1,2*n+1); Wm(1) = lambda / (n + lambda); Wc(1) = Wm(1) + (1 - alpha^2 + beta); for i = 2 : 2*n+1 Wm(i) = 1 / (2 * (n + lambda)); Wc(i) = Wm(i); end %} L = chol(P, 'lower'); X = [mu, mu + sqrt(n+1)*L, mu - sqrt(n+1)*L]; %得到原始均值周围的点作为待处理点 Y = zeros(size(X)); %待处理点过非线性函数 for i = 1:N newx = X(1,i); newy = X(2,i); Y(1,i) = newx+newy; Y(2,i) = 5*newx.^2+newy.^2; end mu_hat = Y * Wm'; %均值加权平均 P_hat = (Y - mu_hat) * diag(Wc) * (Y - mu_hat)'; %方差加权平均 for i=1:N plot(X(1,i),X(2,i),'bo'); end legend('原始数据点','原始数据均值','ut变换选取的待处理点'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% xpar = x + y; %如果所有数据点都过非线性函数再求均值,那就是粒子滤波了 ypar = 5*x.^2+y.^2; figure; plot(xpar,ypar,'r.') hold on; plot(mean(xpar),mean(ypar),'g*') xmean = mu(1) + mu(2); %原始数据点的均值过非线性函数得到的新分布的均值是不对的 ymean = 5*mu(1).^2 + mu(2)^2; plot(xmean,ymean,'b*'); for i=1:N plot(Y(1,i),Y(2,i),'bo'); end plot(mu_hat(1),mu_hat(2),'go'); legend('非线性函数处理后的原始数据点','非线性函数处理后的原始数据点的均值', ... '原始数据点的均值过非线性函数后的值','ut变换选取的待处理点过非线性函数后的值','ut变换最终结果(应该是绿圈,算bug吗。。。)');
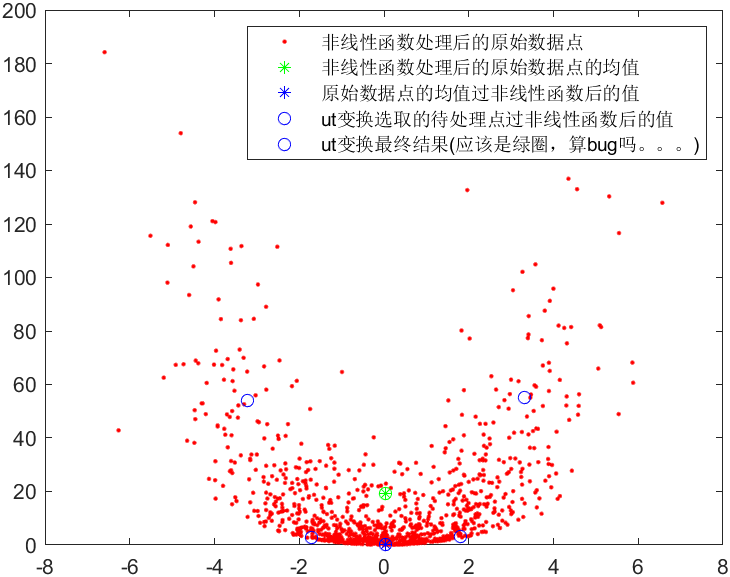
结果如下: