matlab练习程序(球谐拟合)
球谐函数是拉普拉斯方程的球坐标系形式解的角度部分,在古典场论、量子力学等领域广泛应用,在计算机图形学里面可以模拟环境光照。
球谐函数$Y_{l}^{m}$可以表示为:
$Y_{l}^{m}(\theta ,\varphi )=(-1)^{m}\sqrt{\frac{(2l+1))}{4\pi }\frac{(l-|m|)!}{(l+|m|)!}}P_{l}^{m}(cos\theta )e^{im\varphi }$
其中,$l$为自然数,$m$为小于或等于$l$的整数,$P_{l}^{m}$是伴随勒让德多项式,表示为:
$P_{l}^{m}(x)=(-1)^{m}(1-x^{2})^{|m|/2}\frac{d^{|m|}P_{l}(x)}{dx^{|m|}}$
其中,$P_{l}(x)$是$l$阶勒让德多项式,可用罗德里格斯公式表示为:
$P_{l}(x)=\frac{1}{2^{l}l!}\frac{d^{l}}{dx^{l}}(x^{2}-1)^{l}$
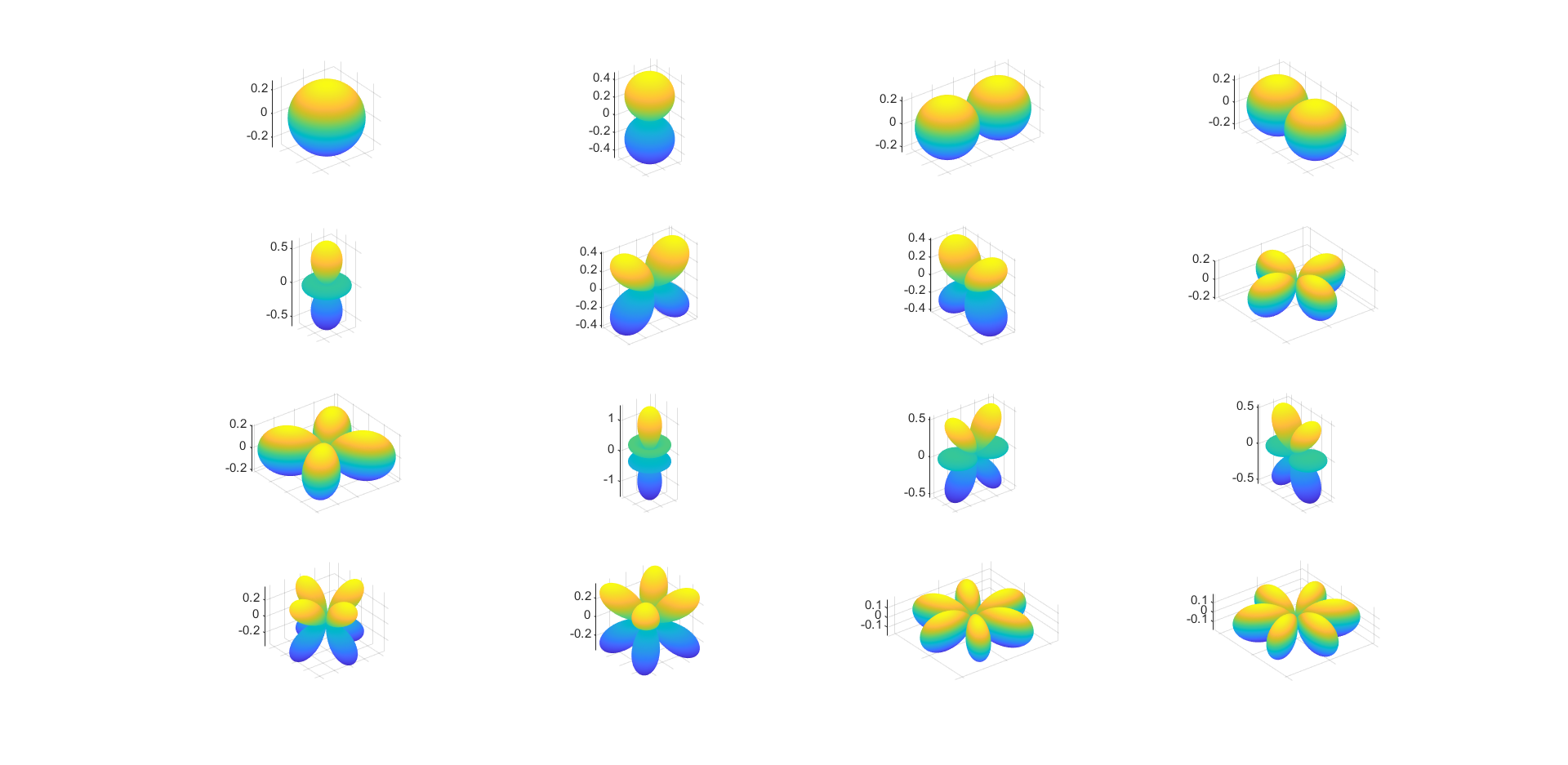
根据不同的$l$和$m$可以得到下列球谐函数表:
 |  | 极坐标中的表达式 | 直角坐标中的表达式 |
|---|---|---|---|
| 0 | 0 | $\frac{1}{2\sqrt{\pi}}$ | $\frac{1}{2\sqrt{\pi}}$ |
| 1 | 0 | $\frac{1}{2}\sqrt{\frac{3}{\pi }}cos\theta$ | $\frac{1}{2}\sqrt{\frac{3}{\pi }}\frac{z}{r}$ |
| 1 | +1 | $\frac{1}{2}\sqrt{\frac{3}{\pi }}sin\theta cos\varphi $ | $\frac{1}{2}\sqrt{\frac{3}{\pi }}\frac{x}{r}$ |
| 1 | -1 | $\frac{1}{2}\sqrt{\frac{3}{\pi }}sin\theta sin\varphi $ | $\frac{1}{2}\sqrt{\frac{3}{\pi }}\frac{y}{r}$ |
| 2 | 0 | $\frac{1}{4}\sqrt{\frac{5}{\pi }}(3cos^{2}\theta -1)$ | $\frac{1}{4}\sqrt{\frac{5}{\pi }}\frac{2z^{2}-x^{2}-y^{2}}{r^{2}}$ |
| 2 | +1 | $\frac{1}{2}\sqrt{\frac{15}{\pi }}sin\theta cos\theta cos\varphi $ | $\frac{1}{2}\sqrt{\frac{15}{\pi }}\frac{zx}{r^{2}}$ |
| 2 | -1 | $\frac{1}{2}\sqrt{\frac{15}{\pi }}sin\theta cos\theta sin\varphi $ | $\frac{1}{2}\sqrt{\frac{15}{\pi }}\frac{yz}{r^{2}}$ |
| 2 | +2 | $\frac{1}{4}\sqrt{\frac{15}{\pi }}sin^{2}\theta cos2\varphi $ | $\frac{1}{2}\sqrt{\frac{15}{\pi }}\frac{x^{2}-y^{2}}{r^{2}}$ |
| 2 | -2 | $\frac{1}{4}\sqrt{\frac{15}{\pi }}sin^{2}\theta sin2\varphi $ | $\frac{1}{2}\sqrt{\frac{15}{\pi }}\frac{xy}{r^{2}}$ |
| 3 | 0 | $\frac{1}{4}\sqrt{\frac{7}{\pi }}(5cos^{3}\theta -3cos\theta )$ | $\frac{1}{4}\sqrt{\frac{7}{\pi }}\frac{z(2z^{2}-3x^{2}-3y^{2})}{r^{3}}$ |
| 3 | +1 | $\frac{1}{4}\sqrt{\frac{21}{2\pi }}(5cos^{2}\theta -1)sin\theta cos\varphi$ | $\frac{1}{4}\sqrt{\frac{21}{2\pi }}\frac{x(5z^{2}-r^{2})}{r^{3}}$ |
| 3 | -1 | $\frac{1}{4}\sqrt{\frac{21}{2\pi }}(5cos^{2}\theta -1)sin\theta sin\varphi $ | $\frac{1}{4}\sqrt{\frac{21}{2\pi }}\frac{y(5z^{2}-r^{2})}{r^{3}}$ |
| 3 | +2 | $\frac{1}{4}\sqrt{\frac{105}{\pi }}cos\theta sin^{2}\theta cos2\varphi $ | $\frac{1}{4}\sqrt{\frac{105}{\pi }}\frac{z(x^{2}-y^{2})}{r^{3}}$ |
| 3 | -2 | $\frac{1}{4}\sqrt{\frac{105}{\pi }}cos\theta sin^{2}\theta sin2\varphi $ | $\frac{1}{2}\sqrt{\frac{105}{\pi }}\frac{xyz}{r^{3}}$ |
| 3 | +3 | $\frac{1}{4}\sqrt{\frac{35}{2\pi }}sin^{3}\theta cos3\varphi $ | $\frac{1}{4}\sqrt{\frac{35}{2\pi }}\frac{x(x^{2}-3y^{2})}{r^{3}}$ |
| 3 | -3 | $\frac{1}{4}\sqrt{\frac{35}{2\pi }}sin^{3}\theta sin3\varphi $ | $\frac{1}{4}\sqrt{\frac{35}{2\pi }}\frac{y(3x^{2}-y^{2})}{r^{3}}$ |
下面给一个全景图,可以用球谐拟合的方式得到环境光照。
matlab代码如下:
clear all;close all;clc; target_img = rgb2gray(imread('sphere.jpg')); target_img = imresize(target_img,[315 629]); imshow(target_img); B = double(target_img(:)); A = zeros(length(B),16); figure; for i=1:16 [fi,theta] = meshgrid(0:0.01:2*pi,0:0.01:pi); x = sin(theta).*cos(fi); y = sin(theta).*sin(fi); z = cos(theta); img = (spherical_polynomials(i,x,y,z)); A(:,i) = img(:); subplot(4,4,i); X = sin(theta).*cos(fi).*abs(img); Y = sin(theta).*sin(fi).*abs(img); Z = cos(theta).*abs(img); mesh(X,Y,Z); axis equal; ax=gca; ax.XAxis.Visible='off'; ax.YAxis.Visible='off'; end x = inv(A'*A)*A'*B; fit_img = zeros(size(target_img)); for i=1:16 fit_img = fit_img + x(i)*reshape(A(:,i),size(target_img)); end figure; imshow(fit_img,[]); function re = spherical_polynomials(n,x,y,z) switch n case 1 re = ones(size(x))/(2*sqrt(pi)); case 2 re = 1/2*sqrt(3/pi)*z; case 3 re = 1/2*sqrt(3/pi)*x; case 4 re = 1/2*sqrt(3/pi)*y; case 5 re = 1/4*sqrt(5/pi)*(2*z.^2-x.^2-y.^2); case 6 re = 1/2*sqrt(15/pi)*(z.*x); case 7 re = 1/2*sqrt(15/pi)*(y.*z); case 8 re = 1/4*sqrt(15/pi)*(x.^2-y.^2); case 9 re = 1/2*sqrt(15/pi)*(x.*y); case 10 re = 1/2*sqrt(7/pi)*(z.*(2*z.^2-3*x.^2-3*y.^2)); case 11 re = 1/4*sqrt(21/(2*pi))*(x.*(5*z.^2-1)); case 12 re = 1/4*sqrt(21/(2*pi))*(y.*(5*z.^2-1)); case 13 re = 1/4*sqrt(105/pi)*(z.*(x.^2-y.^2)); case 14 re = 1/2*sqrt(105/pi)*(x.*y.*z); case 15 re = 1/4*sqrt(35/(2*pi))*(x.*(x.^2-3*y.^2)); case 16 re = 1/4*sqrt(35/(2*pi))*(y.*(3*x.^2-y.^2)); end end
结果如下:
前16个球谐函数:
待拟合光照图像:

球谐拟合光照图像:

参考:



