matlab练习程序（航向角更新）

如果获得了当前时刻的航向角和角速度，需要外推出下一时刻的航向角，这里尝试六种方法计算。

1. 利用角速度和时间直接累积求和得到航向角。

2. 将航向角和角速度都转换到旋转矩阵，通过矩阵相乘得到航向角。

3. 将角速度计算反对称矩阵，再通过指数变换转为李群，在李群上相乘得到航向角。

4. 将角速度计算反对称矩阵，直接在李代数空间相加求和，最后转为李群相乘得到航向角。

5. 将航向角转为四元数，利用一阶航向角积分的毕卡算法得到航向角。

6. 将航向角转为四元数，利用四阶龙科库塔法积分得到航向角。

matlab代码如下：

clear all;close all;clc;

dt = 0.02;                              %准备数据
t = 0:dt:10;
num = length(t);

yawrate1 = rand(int32(num/2)-1,1)*0.5;
yawrate2 = rand(int32(num/2),1)*0.5-0.3;
yawrate=[yawrate1;yawrate2];

re1=zeros(num,1);
re2=zeros(num,1);
re3=zeros(num,1);
re4=zeros(num,1);
re5=zeros(num,1);
re6=zeros(num,1);

startyaw = 0;
%角速度直接求和求旋转角(欧拉角视角)
yaw = startyaw;
for i=1:num
    yaw = yaw + dt*yawrate(i);
    re1(i) = yaw;
end

%角速度通过旋转矩阵相乘求旋转角（旋转矩阵视角）
R = angle2dcm(startyaw,0,0);
for i=1:num
    R = R*angle2dcm(dt*yawrate(i),0,0);
    [yaw,~,~] = dcm2angle(R);
    re2(i) = yaw;
end

%角速度通过反对称矩阵的指数矩阵相乘求旋转角(李群视角)
R = angle2dcm(startyaw,0,0);
for i=1:num
    H = hat([0 0 dt*yawrate(i)])';
    R = R*expm(H);
    [yaw,~,~] = dcm2angle(R);
    re3(i) = yaw;
end

%角速度通过反对称矩阵相加求旋转角(李代数视角)
R = angle2dcm(startyaw,0,0);
newH = zeros(3,3);
for i=1:num
    H = hat([0 0 dt*yawrate(i)])';
    newH = newH + H;
    newR = R*expm(newH);
    [yaw,~,~] = dcm2angle(newR);
    re4(i) = yaw;
end

%角速度通过四元数求旋转角(四元数视角-毕卡算法)
q = angle2quat(startyaw,0,0)';
for i=1:num
    wx = 0;
    wy = 0;
    wz = yawrate(i);
    q_diff = Quaternion_Diff([wx wy wz],q);
    q = q + dt*q_diff;
    [yaw,~,~] = quat2angle(q');
    re5(i) = yaw;
end

%角速度通过四元数求旋转角(四元数视角-四阶龙格库塔积分)
q = angle2quat(startyaw,0,0)';
for i=1:num
    wx = 0;
    wy = 0;
    wz = yawrate(i);
    q = Quaternion_RungeKutta4(q,[wx wy wz],dt);
    [yaw,~,~] = quat2angle(q');
    re6(i) = yaw;
end

figure;
plot(wrapToPi(re1),'r-o');
hold on;
plot(re2,'r-*');
plot(re3,'b-*');
plot(re4,'g-.');
plot(re5,'b-o');
plot(re6,'g-o');

function H = hat(w)
H = [0       -w(3)   w(2);
    w(3)    0       -w(1);
    -w(2)   w(1)   0];
end

function q = Quaternion_RungeKutta4( q0,gyro,T)
K1 = Quaternion_Diff( gyro,q0);
q1 = q0 + T/2*K1;
K2 = Quaternion_Diff(gyro,q1);
q2 = q0 + T/2*K2;
K3 = Quaternion_Diff(gyro,q2);
q3 = q0 + T*K3;
K4 = Quaternion_Diff(gyro,q3);
q = q0 + T/6*(K1+2*K2+2*K3+K4);
end

function q_diff = Quaternion_Diff( gyro,q)
A = [       0, -gyro(1)/2, -gyro(2)/2, -gyro(3)/2;
    gyro(1)/2,          0,  gyro(3)/2, -gyro(2)/2;
    gyro(2)/2, -gyro(3)/2,          0,  gyro(1)/2;
    gyro(3)/2,  gyro(2)/2, -gyro(1)/2,         0];
q_diff = A*q;
end

结果如下：

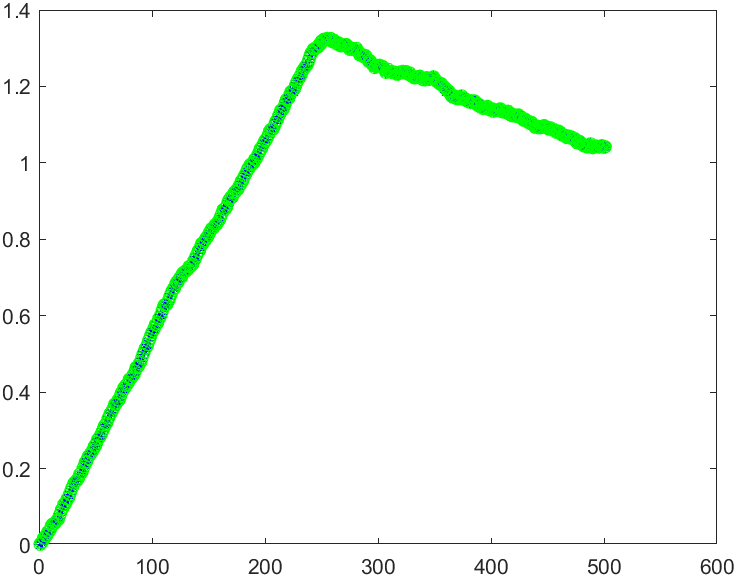
曲线基本重叠了，放大可以看出还是有点区别的。

四元数的两种方法计算似乎都有误差。

不过真实情况是计算方法带来的误差很可能都被噪声淹没了。