matlab练习程序(Z-N法整定)
PID调参时可以先利用Z-N法估算一个大概的量,然后再精确调参。
Z-N法可以形象的用以下图表表示:
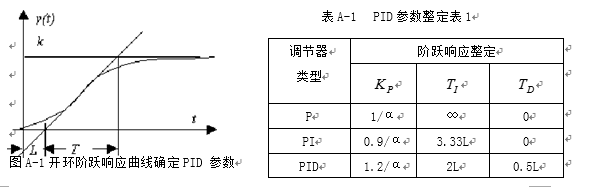
其中切线是响应曲线转折点切线,即过曲线斜率最大点的切线。
K是系统开环稳态响应。
L是转折点切线和0值交点对应的时刻。
L + T是转折点切线和稳态响应交点对应的时刻。
表中的alpha = L / T。
matlab代码如下:
clear all;close all;clc; ts = 0.02; t = 0:ts:10; K = 0.5; sys = tf(1,[2 3 2]); %plant传递函数 c = step(sys,t); subplot(3,1,1); plot(t,c); hold on; plot([0 10],[K K],'r-.'); plot([0 10],[0 0],'r-.'); %微分求得斜率最大值及切线 dc = diff(c); [k,max_x] = max(dc); max_y = c(max_x); max_x = (max_x-1)*ts; k = k/ts; b = max_y - max_x*k; plot(max_x,max_y,'o'); x = 0:0.01:3; y = x*k+b; plot(x,y); %根据切线和两条水平线计算T和tao MaxT = (K-b)/k; tao = (0-b)/k; plot(MaxT,K,'ro'); plot(tao,0,'ro'); T = MaxT-tao; %画出z-n法整定结果 Kp = 1.2*(T/tao); Ti = 2*tao; Td = 0.5*tao; s = tf('s'); G = Kp*(1+1/(Ti*s)+Td*s); subplot(3,1,2); step(feedback(G*sys,1)); %利用pidtune整定 C0 = pidstd(1,1,1); C = pidtune(sys,C0); s = tf('s'); G = C.Kp*(1+1/(C.Ti*s)+C.Td*s); subplot(3,1,3); step(feedback(G*sys,1));
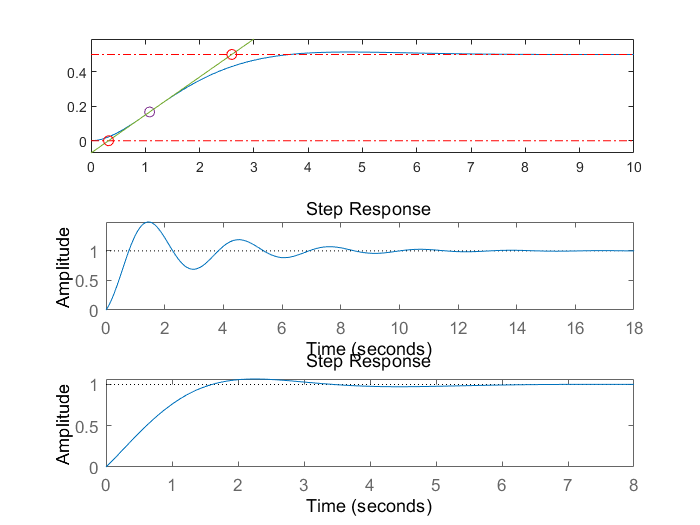
结果如下: