matlab练习程序（ACF/PACF系数计算）

在使用AR/MA/ARMA处理序列之前，需要确定可以使用哪种模型。

通常通过判断ACF或PACF的数据拖尾与截尾情况即可做出判断：

1. 自相关系数拖尾，偏相关系数截尾，选择AR模型。

2. 自相关系数截尾，偏相关系数拖尾，选择MA模型。

3. 两个都拖尾，选择ARMA模型。

这里PACF用的是Yule-Walker方程来求解的，具体原理可以看最后面的链接，感觉讲的很清楚了。

我这里只把代码列出来，并且和matlab做了个比较。

matlab代码如下：

clear;close all;clc;

%AR模型：自相关系数拖尾，偏相关系数截尾
%MA模型：自相关系数截尾，偏相关系数拖尾
%ARMA模型：两个都为拖尾

x = rand(100,1);
for i=3:100
   x(i) = 0.5*x(i-1) + 0.3*x(i-2) + rand(1); 
end

subplot(4,1,1);
plot(x);
title('原数据');

corr = calc_xcorr(x);
subplot(4,1,2);
plot(corr,'g-o')
hold on;
plot(xcorr(x),'r-*')
title('自相关');

acorr=calc_acorr(x);
subplot(4,1,3);
plot(acorr,'g-o');
hold on;
y=xcorr(x-mean(x));
plot(y(length(x):end)/max(y),'r-*');
plot(autocorr(x,length(x)-1),'b');
title('归一化自相关');

pcorr=aclc_pcorr(x);
subplot(4,1,4);
plot(pcorr,'g-o');
hold on;
plot(parcorr(x,'Method','yule-walker','NumLags',length(x)-1),'r-*');
title('偏相关');

%自相关
function corr = calc_xcorr(x)
xinv = flipud(x);
corr = zeros(2*length(x)-1,1);
for i=1:length(x)
    for j=1:i
        corr(i) = corr(i) + x(j)*xinv(i-j+1);
        corr(length(corr)-i+1) = corr(i);
    end
end
end

%归一化后的自相关
function acorr=calc_acorr(x)
x = x - mean(x);
xinv = flipud(x);
acorr = zeros(2*length(x)-1,1);
for i=1:length(x)
    for j=1:i
        acorr(i) = acorr(i) + x(j)*xinv(i-j+1);
        acorr(length(acorr)-i+1) = acorr(i);
    end
end
acorr =acorr(length(x):end)/max(acorr);
end

%偏相关
function pcorr=aclc_pcorr(x)
x = x - mean(x);
pcorr = ones(length(x),1);
for k=2:length(pcorr)
    
    r = zeros(k,1);
    for i=1:k
        r(i) = sum(x(1:length(x)-i+1).*x(i:length(x)))/(length(x));
    end
    R=toeplitz(r(1:end-1));
    
    theta = R\r(2:end);
    pcorr(k) = theta(end);
end
end

结果如下：

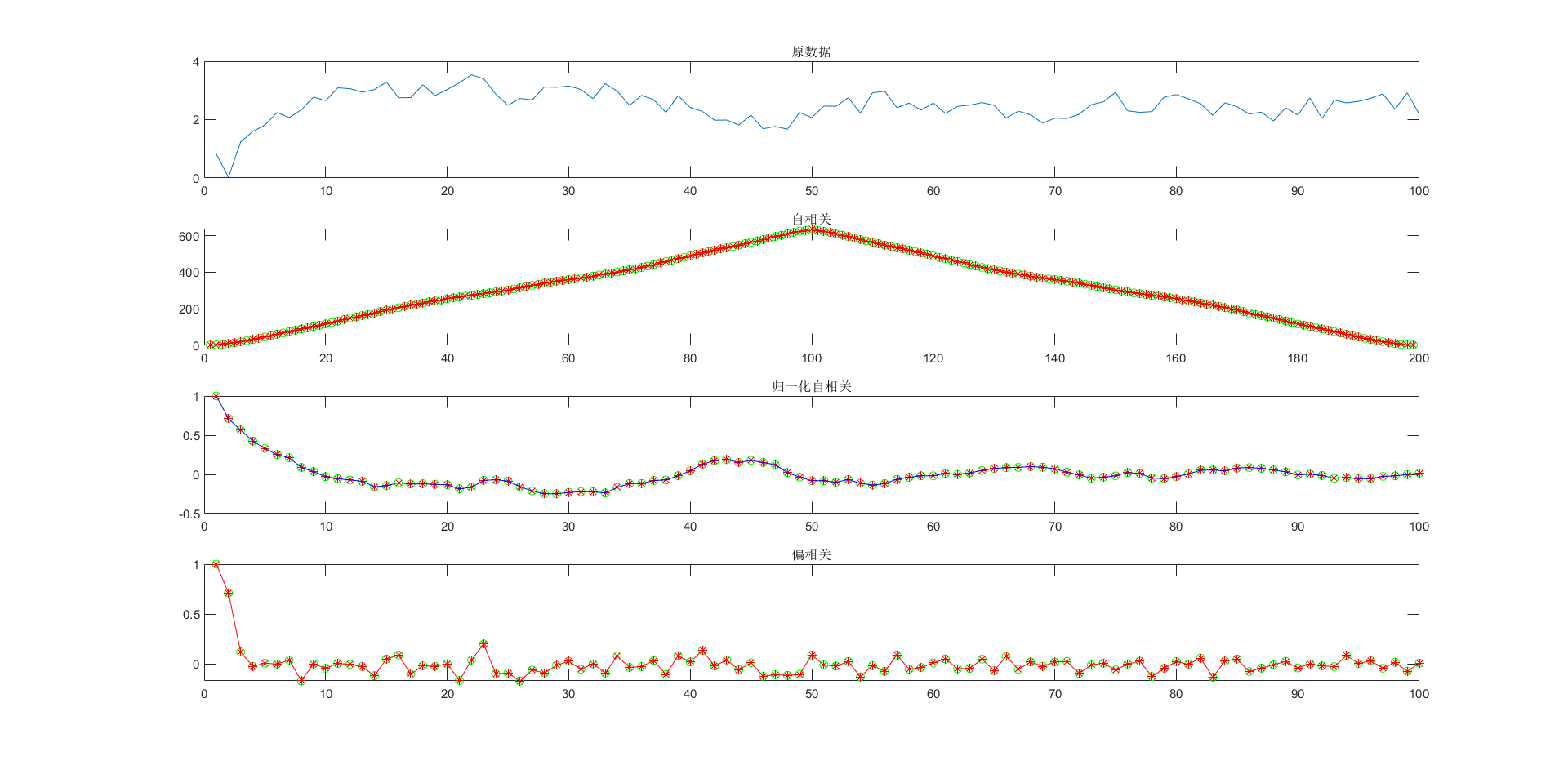
参考：

https://www.jianshu.com/p/811f9ea0b52d

http://www-stat.wharton.upenn.edu/~steele/Courses/956/ResourceDetails/YWSourceFiles/YW-Eshel.pdf