matlab练习程序（离散点平滑算法）

路径平滑方法有很多。

如果有预测量可以使用卡尔曼滤波。

如果只是单纯的离散点也可以用多项式拟合、样条插值、回旋曲线或者均值滤波来平滑。

这里这个算法是Apollo里面的算法，单独拿出来看一下吧。

首先算法是利用最优化的方法来求解的，待优化参数就是所有的离散点（xk,yk)，如下图：

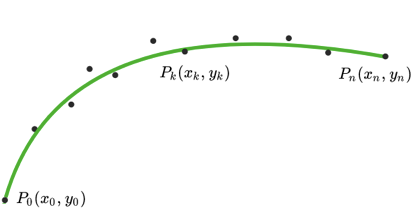设定损失函数为 cost = cost_smooth + cost_length + cost_deviation。

其中cost_smooth为平滑度代价，函数定义为：

 

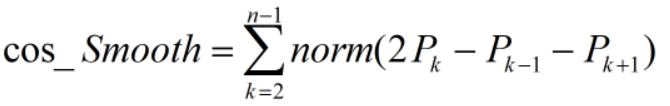
其中cost_length为长度代价，函数定义为：

 

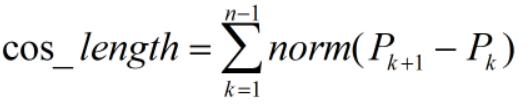
其中cost_deviation为偏离原始点代价，函数定义为： 

 

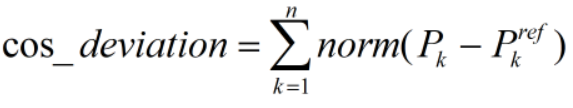
最后迭代优化参数(xk,yk)，最终使其cost最小即可。

下面没有再自己写优化方法了，用的matlab中lsqnonlin方法，其实还是LM优化方法。

matlab代码如下：

clear all;close all;clc;

x = 0.1:0.1:2*pi;
y = sin(x)+log(x).*cos(x) + rand(length(x),1)'*0.5;
x = x + rand(length(x),1)'*0.2;
plot(x,y,'r-o');
axis equal;

Ref = [x' y'];
par = [x' y'];              %待优化参数

options.Algorithm = 'levenberg-marquardt';
f = @(par) func(par,Ref);
lb = [];
ub = [];
[par,res]= lsqnonlin(f,par,lb,ub,options);

hold on;
plot(par(:,1),par(:,2),'g-o');

function re = func(par,Ref)     %构建优化模型，re为损失误差

cost_s = 0;
cost_l = 0;
cost_d = 0;
for i = 2:length(par)-1
    cost_s = cost_s + norm(2 * par(i,:) - par(i-1,:) - par(i+1,:));
    cost_l = cost_l + norm(par(i+1,:) - par(i,:));
    cost_d = cost_d + norm(par(i,:) - Ref(i,:));
end

re = cost_s+cost_l+cost_d;

end

结果如下：

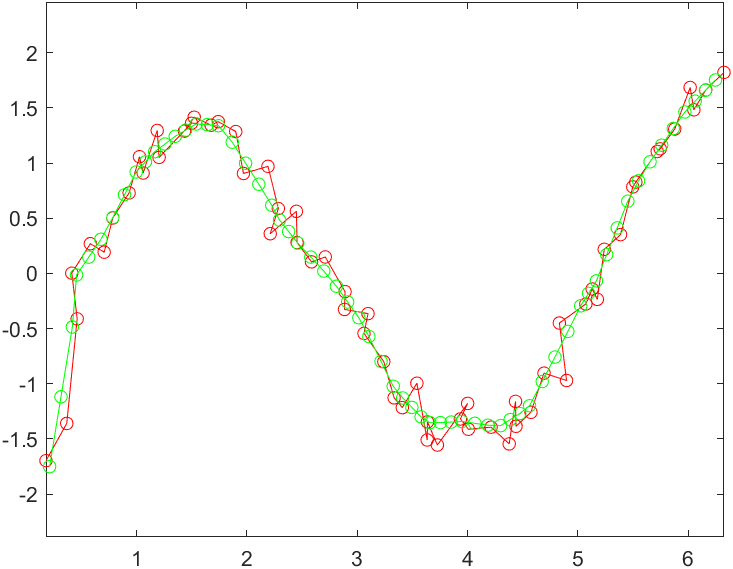
参考：离散点曲线平滑原理