matlab练习程序（Stanley路径跟踪）

方法示意图：

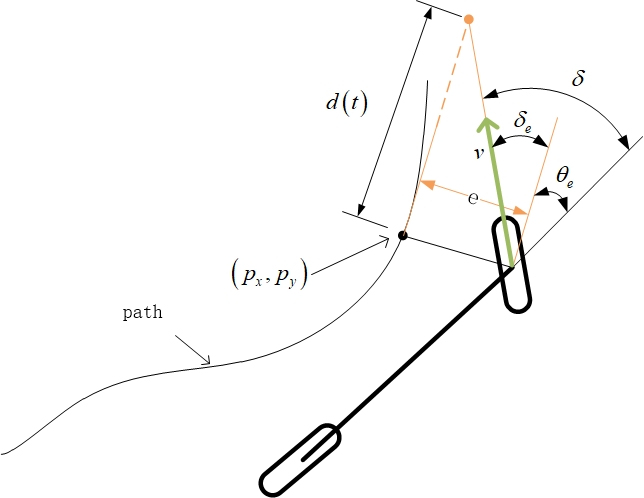
控制率公式：

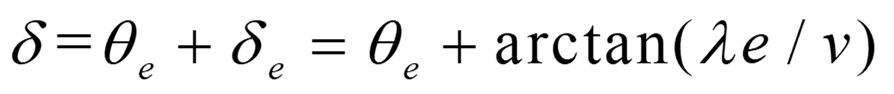
其中theta是当前航向角与路径航向角之差，e为横向误差，v为车辆速度，lambda为控制参数。

算法步骤如下：

1. 根据当前定位结果找到路径最邻近点。

2. 计算该点与定位结果横向误差e与航线误差theta。

3. 根据控制率公式计算出前轮转角。

4. 将前轮转角转化为航向角，带入运动模型计算出下一时刻的位姿。

matlab代码如下：

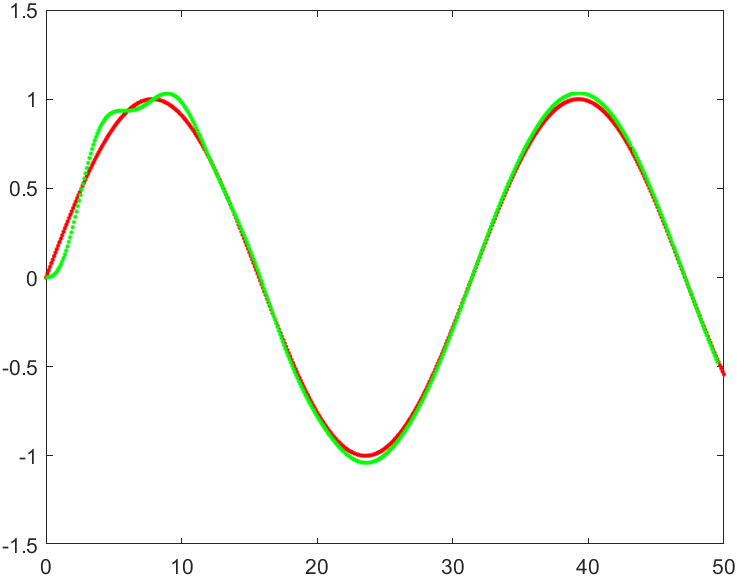
clear all;close all;clc;

v = 1;
lambda = 3;
dt = 0.1;
L=2.5;
curp=[0 0 0];

x = 0:0.1:50;
y = sin(x/5);
path = [x' y'];
for i=2:length(path)
    dx = path(i,1)-path(i-1,1);
    dy = path(i,2)-path(i-1,2);
    path(i-1,3) = atan2(dy,dx);
end
path(length(path),3) = path(length(path)-1,3);
plot(path(:,1),path(:,2),'r.');
hold on;

for i=1:length(path)
    
    d = path(:,1:2) - curp(1:2);
    dis = d(:,1).^2 + d(:,2).^2;
    [~,ind] = min(dis);                                     %找路径最近点索引
    
    dx = curp(1) - path(ind,1);
    dy = curp(2) - path(ind,2);
    
    e = (sin(curp(3) - atan2(dy,dx)))*sqrt(dx*dx+dy*dy);    %横向偏差
    u = (path(ind,3) - curp(3)) + atan2(lambda*e,v);        %期望前轮转角
    
    curp(1) = curp(1) + dt*v*cos(curp(3));
    curp(2) = curp(2) + dt*v*sin(curp(3));
    curp(3) = curp(3) + dt*v*tan(u)/L;
    
    plot(curp(1),curp(2),'g.');
end

结果如下：

绿色为跟踪路径，红色为已知路径。

参考：

https://blog.csdn.net/renyushuai900/article/details/98460758

https://windses.blog.csdn.net/article/details/103518011