matlab练习程序（数值雅克比）

数值雅克比本质就是对函数的每一维分别做数值微分，再组合为雅克比矩阵即可。

通常我们做最优化的时候要计算函数的雅克比矩阵，但是如果函数的解析式比较复杂，求其偏导解析解会非常麻烦。

虽然可以利用Mathematica或者Matlab的符号运算进行求解，不过有时候得到的解析解也是很复杂的，再转写成代码如果错一个符号很可能就找不到错误来源了。

利用数值方法求偏导，得到雅克比矩阵，在进行优化求解，通常可以简化整个过程。

下面用之前文章中高斯牛顿法优化作为例子，来实践一下如何计算数值雅克比。

matlab代码如下：

clear all;close all;clc;

epsilon = 1e-6;
epsilon_inv = 1/epsilon;

a=1;b=2;c=1;                        %待求解的系数
x = (0:0.01:1)';
w = rand(length(x),1)*2-1;          %生成噪声
y = exp(a*x.^2+b*x+c) + w;          %带噪声的模型 
plot(x,y,'.')

pre=rand(3,1);                      %步骤1
for i=1:100
    
    f0 = exp(pre(1)*x.^2+pre(2)*x+pre(3));
    g = y - f0;                     %步骤2中的误差 
         
    %数值计算雅克比
    for k = 1:length(pre)
        x_ = pre;
        x_(k) = pre(k) + epsilon;
        jac(:, k) = (exp(x_(1)*x.^2+x_(2)*x+x_(3)) - f0) .* epsilon_inv;
    end
    J = jac;
    
    delta = inv(J'*J)*J'* g;        %步骤3，inv(J'*J)*J'为H的逆
    
    pcur = pre+delta;               %步骤4
    if norm(delta) <1e-16
        break;
    end
    pre = pcur;
end

hold on;
plot(x,exp(a*x.^2+b*x+c),'r');
plot(x,exp(pre(1)*x.^2+pre(2)*x+pre(3)),'g');

%比较一下
[a b c]
pre'

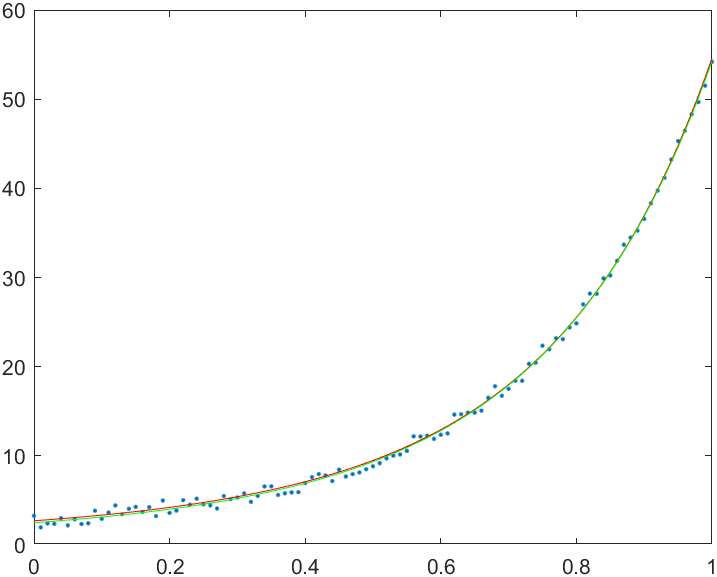
结果如下：