matlab练习程序（B样条反算控制点）

如果要准确反求B样条的控制点，有几个参数还是要事先知道的：

1. 样条的控制点个数。

2. B样条曲线的所有点坐标和个数。

3. B样条基函数。

一般条件2容易知道一些，1和3还是比较难事先知道的。

如果待求控制点为四个，B样条曲线点个数为n个，并且已知基函数形式如下面代码中[b0 b1 b2]。

则可以列出类似下面这样一个方程组求解，其中px,py为带求解控制点，x、y为B样条曲线点：

matlab代码如下：

clear all;close all;clc;

p =ginput();  
plot(p(:,1),p(:,2),'g-o');  

p
%二次均匀b样条
re=[];
for i=1:length(p)-2  
    for t=0:0.1:1   
        
        b0 = 1/2*(1-t)^2;
        b1 = 1/2*(-2*t^2+2*t+1);
        b2 = 1/2*t^2;
        
        x=b0*p(i,1)+b1*p(i+1,1)+b2*p(i+2,1);
        y=b0*p(i,2)+b1*p(i+1,2)+b2*p(i+2,2);        
        
        re=[re;x y];
    end
end

hold on;  
plot(re(:,1),re(:,2),'r-o');

%构造方程求解
n = length(p);
step = length(re) / (n-2);
A = zeros(length(re)*2,n*2);
B = zeros(length(re)*2,1);
t = linspace(0,1,step); 
for i=1:n-2
    for j=1:length(t)
        b0 = 1/2*(1-t(j))^2;
        b1 = 1/2*(-2*t(j)^2+2*t(j)+1);
        b2 = 1/2*t(j)^2;  
        
        A((j-1)*2+1+(i-1)*length(t)*2,1+(i-1)*2) = b0;
        A((j-1)*2+1+(i-1)*length(t)*2,3+(i-1)*2) = b1;
        A((j-1)*2+1+(i-1)*length(t)*2,5+(i-1)*2) = b2;
        A((j-1)*2+2+(i-1)*length(t)*2,2+(i-1)*2) = b0;        
        A((j-1)*2+2+(i-1)*length(t)*2,4+(i-1)*2) = b1;
        A((j-1)*2+2+(i-1)*length(t)*2,6+(i-1)*2) = b2;        
        
        B((j-1)*2+1+(i-1)*length(t)*2) = re(j+(i-1)*length(t),1);
        B((j-1)*2+2+(i-1)*length(t)*2) = re(j+(i-1)*length(t),2); 
    end
end

X = inv(A'*A)*A'*B;

%画出新曲线看看
figure;
p = reshape(X,[2 length(X)/2])'
plot(p(:,1),p(:,2),'g-*');  
re=[];
for i=1:length(p)-2  
    for t=0:0.1:1   
        
        b0 = 1/2*(1-t)^2;
        b1 = 1/2*(-2*t^2+2*t+1);
        b2 = 1/2*t^2;
        
        x=b0*p(i,1)+b1*p(i+1,1)+b2*p(i+2,1);
        y=b0*p(i,2)+b1*p(i+1,2)+b2*p(i+2,2);        
        
        re=[re;x y];
    end
end

hold on;  
plot(re(:,1),re(:,2),'r-*');

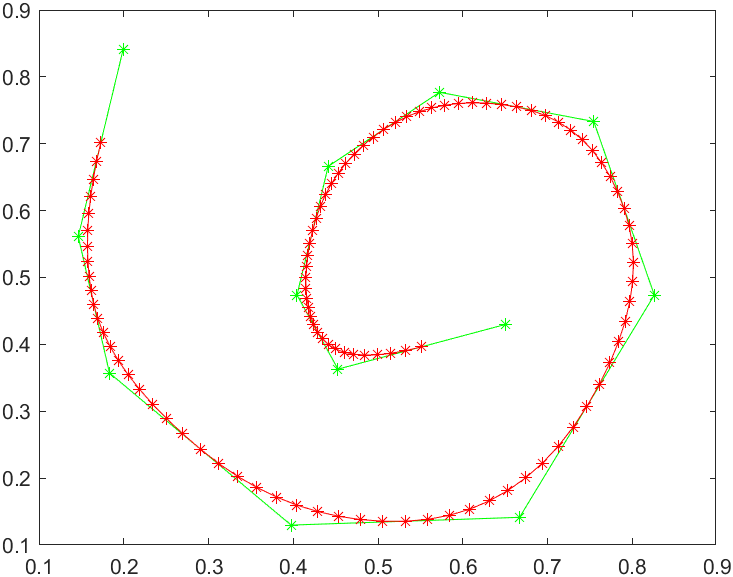
结果如下：

原始B样条曲线：

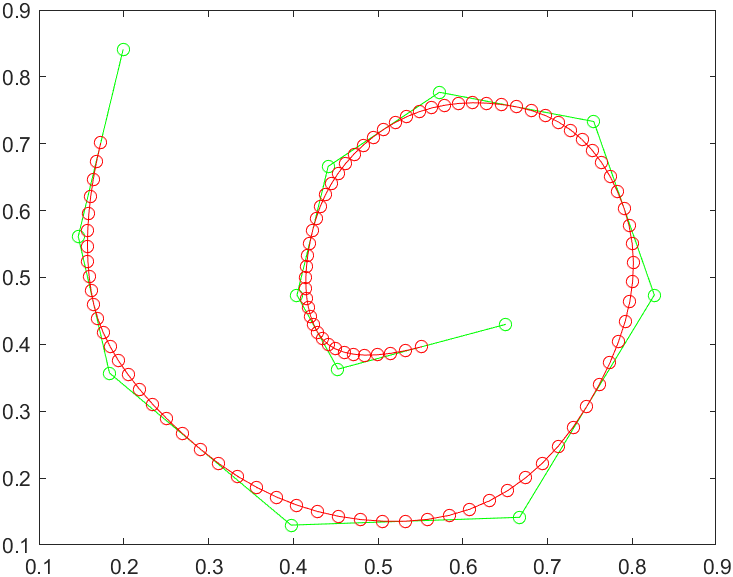
反求解控制点后生成的B样条曲线：