matlab练习程序（Douglas-Peuker算法）

该算法可以抽稀路径上的数据，在保证几何形状基本不变的情况下，最大限度去除冗余点。

算法逻辑如下：

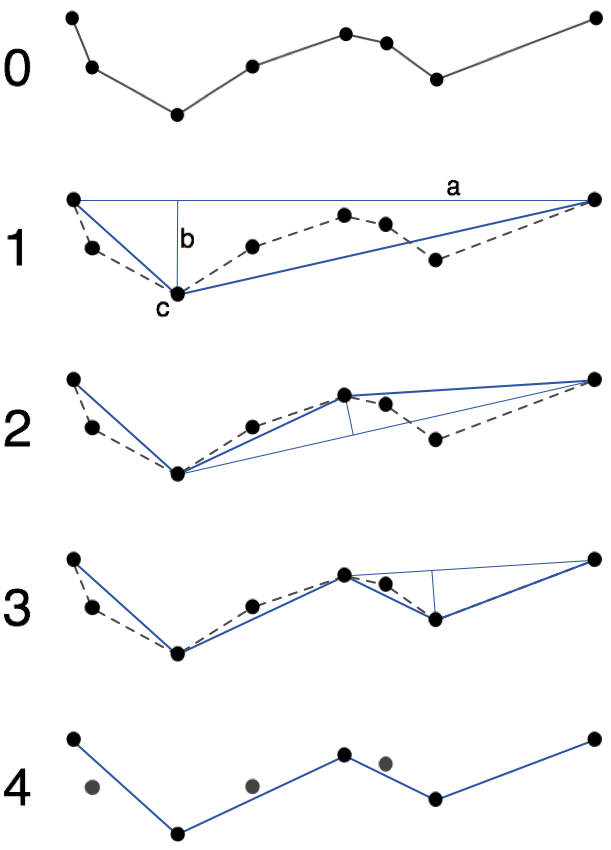
（1）在曲线首尾两点A，B之间连接一条直线AB，该直线为曲线的弦；

（2）得到曲线上离该直线段距离最大的点C，计算其与AB的距离d；

（3）比较该距离与预先给定的阈值threshold的大小，如果小于threshold，则该直线段作为曲线的近似，该段曲线处理完毕。

（4）如果距离大于阈值，则用C将曲线分为两段AC和BC，并分别对两段取信进行1~3的处理。

（5）当所有曲线都处理完毕时，依次连接各个分割点形成的折线，即可以作为曲线的近似。

代码如下：

clear all;close all;clc;

err = 0.01;                         %设置最大偏离距离

x = 0:0.01:5;
y = sin(x);
path = [x' y'];
plot(path(:,1),path(:,2),'r-o');

flag = zeros(length(path),1);       %设置可以采用的点索引标志
stack = [1 length(path)];

while ~isempty(stack)
    ind = stack(1,:);               %取栈首数据
    stack(1,:) = [];
    Q1 = path(ind(1),:);          %起始位置
    Q2 = path(ind(2),:);
    dmax = -1;
    for i=ind(1):ind(2)
        P = path(i,:);
        d = abs(det([Q2-Q1;P-Q1]))/norm(Q2-Q1); %P点到Q1-Q2直线距离
        
        if d >= dmax                %取距离最大的点的索引
            dmax = d;
            index = i;
        end
    end
    
    if dmax >= err
        stack = [stack;ind(1) index];       %压栈
        stack = [stack;index ind(2)];
    else
        flag(ind(1)) = 1;                   %标记被选中的点的索引
        flag(ind(2)) = 1;
    end
end

newpath = path(flag==1,:);
hold on;
plot(newpath(:,1),newpath(:,2),'g-*');

结果如下：

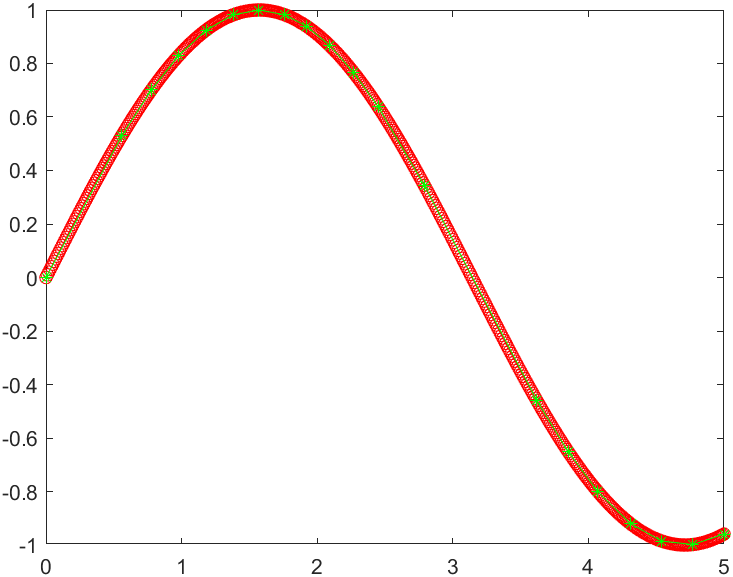
其中红线为原始曲线，绿线为采样后曲线。